Explore the fascinating world of the Banach Limit, a mathematical tool that extends the concept of limits beyond convergent sequences, assigning a limit value to sequences that might otherwise seem ‘limitless’.

ADVERTISEMENT

Explore the fascinating world of the Banach Limit, a mathematical tool that extends the concept of limits beyond convergent sequences, assigning a limit value to sequences that might otherwise seem ‘limitless’.

Explore the intricacies of Stochastic convergence, a vital concept in probability theory. Learn about the different types and their applications in statistics and stochastic processes.

A **Convergent Matrix** is a square matrix that converges to the zero matrix when raised to successive powers. This article explores the properties of these matrices and their importance in iterative methods.

Category theory limits provide a unified way to describe and relate various mathematical structures. This post explains how category theory limits are fundamental tools for understanding complex mathematical ideas.
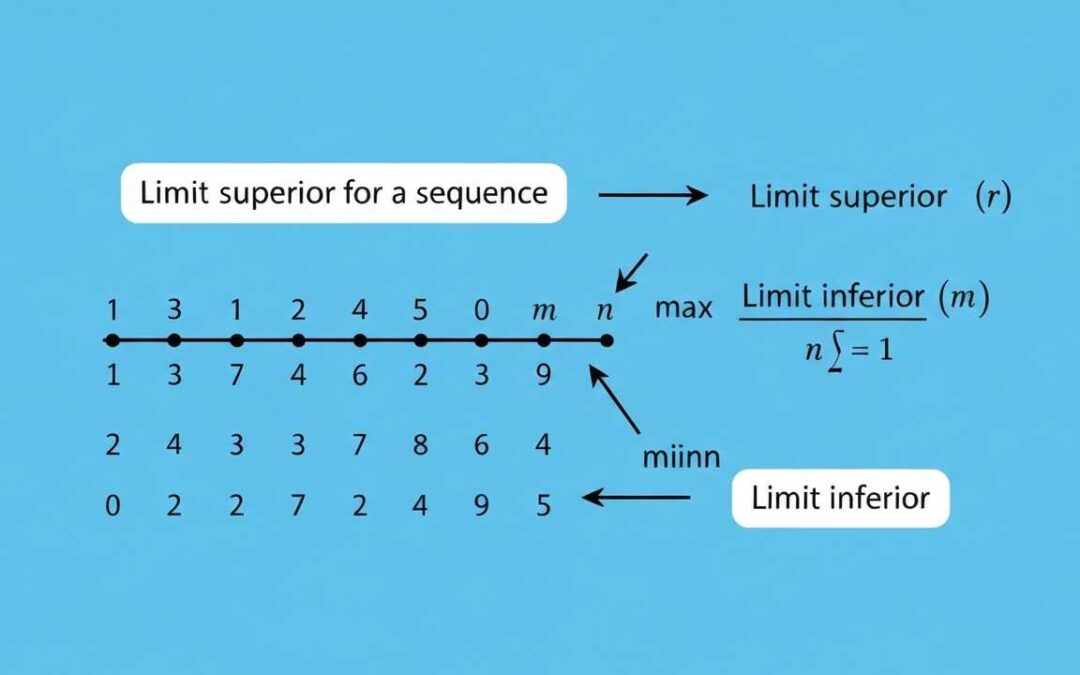
Understand Limit Superior and Inferior: Learn how these concepts define the eventual bounds of sequences and functions, and their importance in mathematical analysis.

Understanding the different **types of convergence** is essential in mathematics. From sequences and series to functions, this post explores the various modes of convergence.

Profit and loss questions improve real-world calculation ability.

Probability is key in logical and math aptitude exams.

Men working together to complete tasks faster is a common aptitude question.

Profit and loss questions test practical business math.
Collaboration work problems are frequently tested in exams.

Interest problems are critical in finance-related aptitude tests.
Averages are tested often in aptitude exams with practical twists.
Number series problems improve pattern recognition for competitive exams.
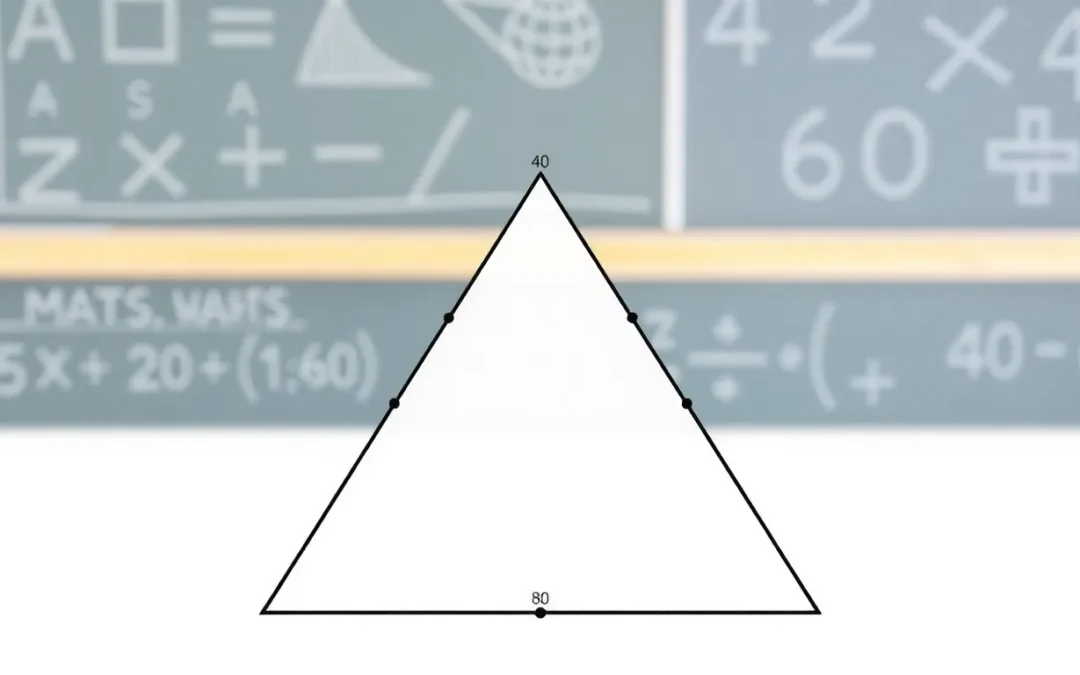
Triangle angle ratio questions build geometry fundamentals.

Learn the basics! This post answers the question: What is a plane?
This post explores the Sum of Series Formula, showing you how to derive and apply it to solve complex series problems. You’ll learn the formula and see examples.
Learn how to solve trigonometric problems by understanding and applying Trigonometric Identities. We break down the steps to find ##\sin^3 \theta + \cos^3 \theta## when given ##\sin \theta + \cos \theta = \frac{5}{4}##.

Learn about **GCD calculation** and the Euclidean algorithm. This post provides a step-by-step guide to finding the greatest common divisor of two numbers, crucial in various mathematical applications.

Learn how to calculate the Probability of Rolling a 7 with our easy-to-follow guide. Understand the step-by-step process and the math behind it.
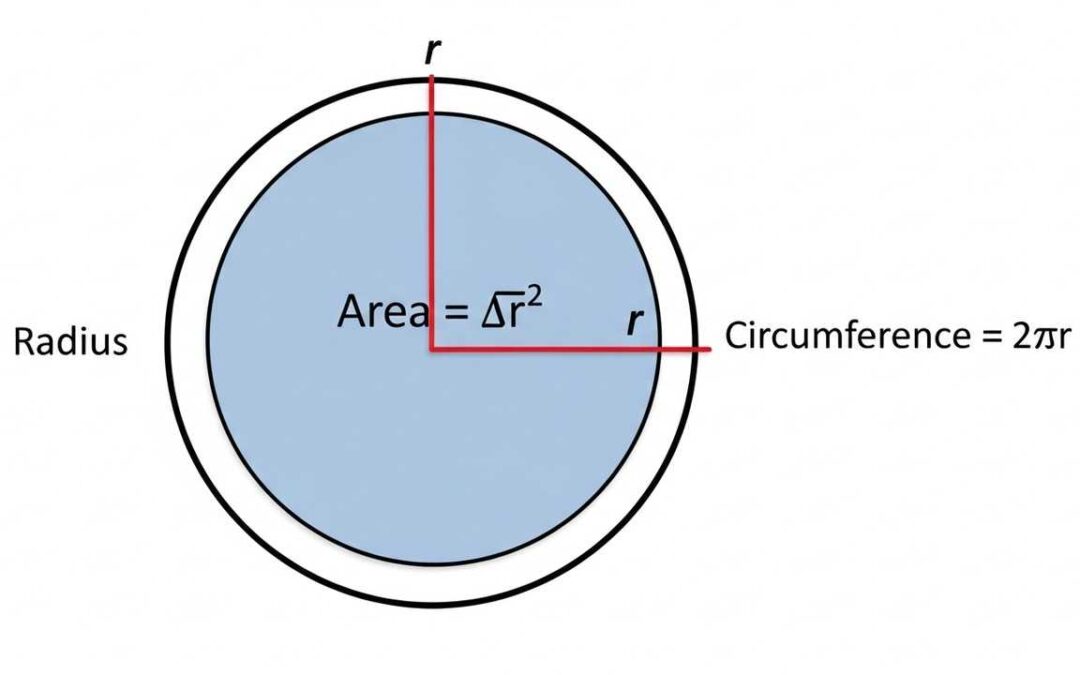
Learn how to calculate the **circle area and circumference** with a given radius using simple formulas and step-by-step examples. We’ll break down the process for easy understanding.

Learn how to **solve quadratic equations** using factoring and the quadratic formula. Discover the roots and understand the different methods with examples.

Explore how function behavior changes with large variables. Learn to identify warning signs and avoid common pitfalls in mathematical analysis.

Learn how to prove that a function is bounded with this step-by-step guide. Master the techniques for a bounded function proof.

Discover which functions have compositional square roots! Learn about bijections, cycle decomposition, and how to find these roots.

Explore the divisibility by floor square root problem. Find all integers ##n## where ##\lfloor{\sqrt{n}}\rfloor \mid n##. Solutions and examples included.

Learn fuzzy logic aggregation techniques to combine uncertain data. Enhance decision-making and risk assessment with fuzzy values.

Understanding derivatives simply involves grasping how functions change. This guide offers an intuitive explanation for beginners.

Explore the ramp function, its definition, properties, and applications in signal processing and control systems. Understand the ramp function today!

Explore surjective function composition with clear examples. Learn when the composition of surjective functions remains surjective and when it doesn’t.

Explore the function codomain, its definition, and why it’s crucial in math. Understand its role in function composition and surjectivity.

Learn how to perform function decomposition by separating any function into its even and odd parts, simplifying complex analysis.

Prove that an expression is independent of n using number theory. Explore modular arithmetic and floor functions to show constant results.

Explore arc length functions and their cardinality. Discover how the number of continuous functions changes with increasing arc length.

Explore the conditions for defining integrals, focusing on the necessary structures of spaces and functions for meaningful integration.

Explore the meaning of p-value variance, ##x(1-x)##, in statistics. Learn how it relates to Bernoulli distribution and its applications.

Explore the formulas behind common crossfader curves like Dipped, Constant Power, and Linear. Enhance your DJ mixing skills today!

Explore L-structures in first-order logic, their construction, and counting methods. Understand how L-structures first order logic works with examples.

Learn how to solve function composition problems algebraically with step-by-step solutions. Master the art of decomposing complex functions!

Explore the area of recursive functions with a detailed analysis. Discover how the area remains constant as the recursion depth increases.

Explore function sections, a method to simplify multi-variable functions by fixing one variable. Learn how function sections aid in analysis.

Explore function iteration notation with clear examples. Learn how to represent repeated function compositions effectively and avoid common ambiguities.

Explore function decay rates and how the parameter α affects whether a function has slow or rapid decay. Learn with examples!

Learn how to represent logical operators like AND, OR, and NOT as functions. Understand their mathematical formulations and applications.

Learn how to build functions continuous at specific points, like integers or irrationals. Explore examples and proofs for constructing continuous functions.

Explore proving that the floor function has Theta complexity of Θ(x). Learn about upper and lower bounds in this analysis.
Learn how to efficiently compute the sum of coefficients in the Hadamard product of generating functions. Simplify complex calculations!

Understanding function notation is key! Learn the difference between f(x) and f, and how to use them correctly in math.

Explore fractional differentiability functions and how they behave with non-integer derivatives. Learn about constructing functions with specific differentiability.

Explore generalized cosine functions through functional equations. Understand solutions and challenges in higher-order generalizations.

Learn how to find the minimum value function using calculus. Step-by-step guide included!

Explore the density of smooth functions in L1 and L2 spaces. Learn how smooth functions approximate complex functions effectively.

Learn how to tile piecewise functions diagonally across a grid. This guide provides a clear solution for transforming inputs and achieving the desired tiling effect.

Explore the Mandelbrot set main cardioid, its fixed points, and multipliers. Understand its role in complex dynamics and the Mandelbrot set.

Explore the definition, identification, and applications of prime numbers. Understand why prime numbers are crucial in cryptography and computer science.

Explore the probability of expected rolls to see all sides of a die. Understand why multiple dice don’t simply halve the expectation.

Learn about transformations in coordinate geometry. This guide provides a comprehensive explanation with illustrative examples.

Explore rotations and reflections in coordinate geometry with illustrative examples. Learn the fundamentals in simple language.

Explore the slope-intercept form to simplify linear equations effectively.

Explore the terms abscissa ordinate and applicate in coordinate geometry.

Explore the fundamental concept of a line in geometry. Learn the definition and key properties. What is a line?

Explore the fundamental concept: What is a point? Learn its definition and significance in various contexts.

Learn the basics of Euclidean geometry. This beginner’s guide explains key concepts in an easy-to-understand way.
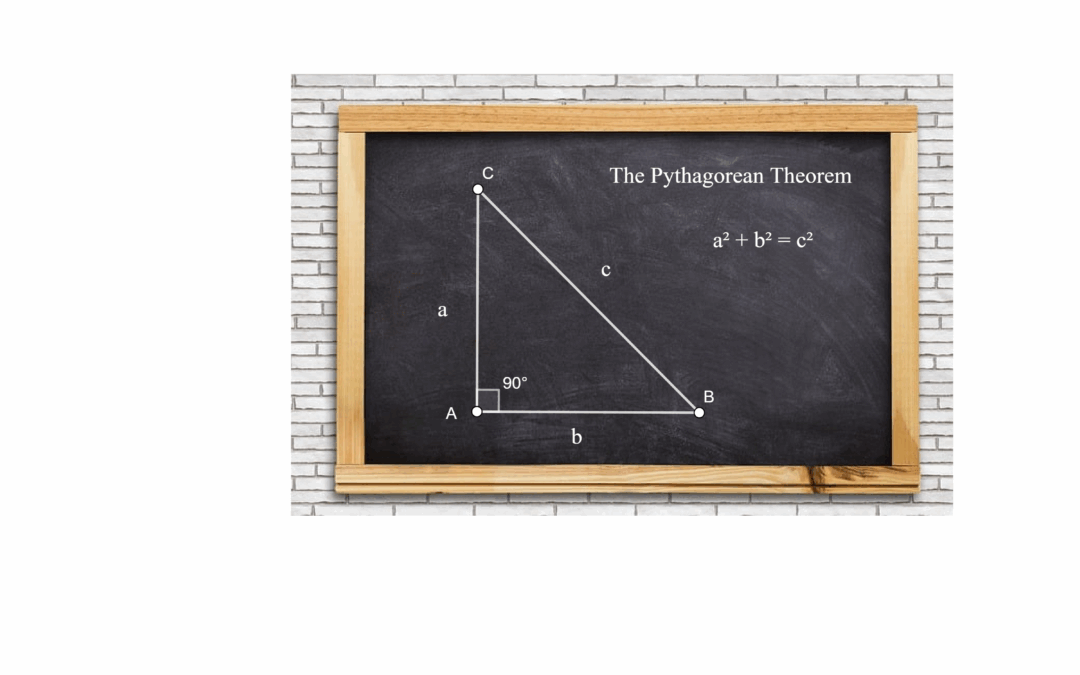
Learn the Pythagorean Theorem! Explore its history proof practical applications and solve 10 problems.

Learn about conic sections! This post explains ellipses parabolas hyperbolas and their properties in detail.
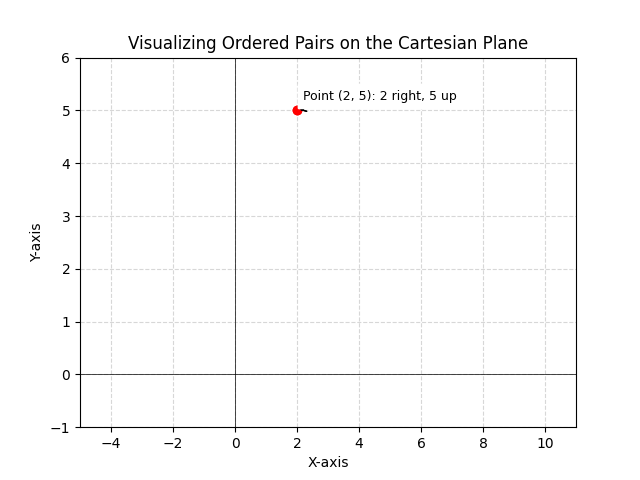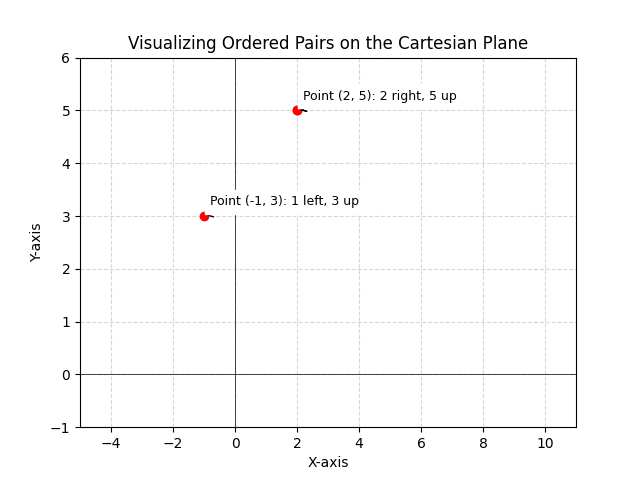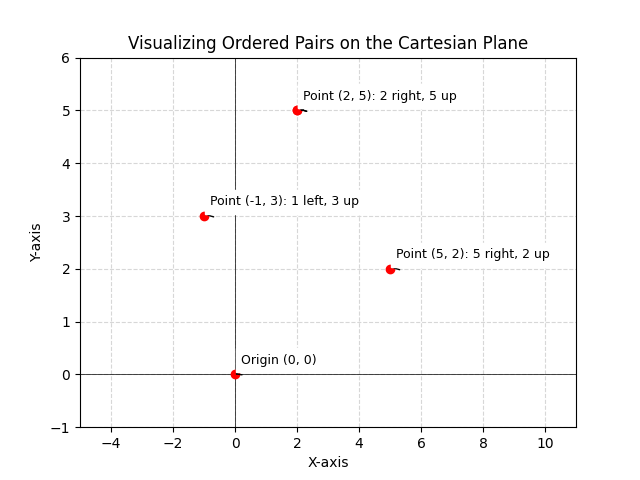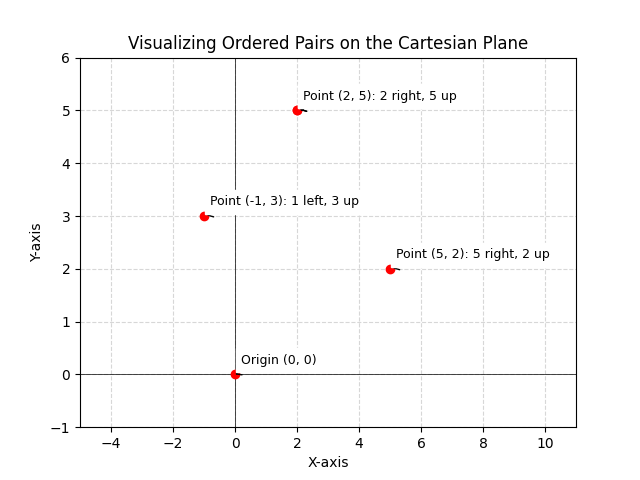
Learn the definition of an ordered pair in mathematics including its key characteristics and applications. Explore examples and understand how it’s used.
Discover how to solve polynomial equations and find q(uv) = 0. Learn techniques for determining polynomial relationships between variables. Polynomial Equation Solver.

Learn how to decompose polynomial matrices using elementary row operations. This guide provides a step-by-step approach to polynomial matrix decomposition.

Explore the inequality concerning the dimension of harmonic homogeneous polynomials. Learn about the relationship between homogeneous polynomials and their Laplacian. Harmonic Homogeneous Polynomials explained.

Investigating the image of a ratio of polynomials with affine coefficients. Does the image lie within a complex polytope defined by vertices? Polynomial Ratio Image.

Discover the fascinating relationship between Chebyshev polynomials of the second kind and binomial coefficients in this exploration of series. Chebyshev Polynomials Series.

Learn how to rewrite a non-commutative product as a sum. This guide explores methods for expanding products of non-commuting elements offering both general formulas and recursive approaches. Non-commutative Product Expansion explained.

Learn how to compute the ideal of a projective algebraic set in P^2(C). This post explores methods for determining the ideal including geometric approaches and Gröbner bases. Projective Algebraic Set Ideal.

Learn how to calculate the change of basis matrix for linear maps on polynomials. This guide clarifies common discrepancies and misunderstandings. Change of Basis Matrix explained.

Discover the top AI tools to boost your productivity and efficiency. Learn about various AI tools.

Learn how the Luhn algorithm validates credit card numbers and other identification codes. Discover the steps and applications of this essential checksum formula.

Learn about Coulomb’s Law the inverse square law of force and how French physicist Charles-Augustin de Coulomb discovered it.

Learn about open and closed intervals in mathematics including definitions and examples. Essential for understanding calculus.

Learn about sequences their limits and how they differ from functions. Discover convergence and divergence and essential theorems.

Learn about open and closed intervals in mathematics including definitions and examples using mathjax notation.

Learn what it means for a series to converge to a specific value in mathematics. Explore the concept of convergence.

Explore if disjoint subsets of natural numbers exist where the sum of harmonic series terms over each subset is equal. Investigate the harmonic series and its subset sums.

Can natural numbers be divided into two sets with equal sums of their digits? Explore this intriguing partitioning problem.

Discover how to find subsets of natural numbers where the sum of reciprocals of their squares is equal exploring both finite and infinite cases.
Learn about arithmetic geometric and harmonic series with 5 examples each. Discover the formulas and how to solve problems.

Learn why the harmonic series despite growing slowly doesn't converge. Explore different explanations for this fascinating mathematical concept.

Discover the fascinating exponential limit of x^x as x approaches 0+. Learn the solution using logarithms and L'Hôpital's rule.

Learn how L'Hôpital's Rule simplifies limit evaluation. This guide will help you solve limits efficiently.

Learn how L'Hôpital's rule helps evaluate indeterminate forms in limits. This guide provides a complete explanation and examples.

Discover the zeroes of the quadratic polynomial passing through specific points.

Explore the inequality coefficients problem for positive real numbers and find possible permutations.

Explore implicit differentiation and its relation to differential equations in our new quiz feedback.

Explore the solutions for distinct real numbers satisfying specific equations in this insightful blog post.

Learn how to calculate distance in 3D using triangular relationships and trigonometric ratios.

Learn how to find the remainder of polynomial division using standard and alternate methods.

Discover exacting and ultraexacting cardinals new types of infinity challenging traditional set theory views and potentially resolving long-standing conjectures.

Learn how to calculate the distance a car travels with uniform acceleration. Find the distance covered in 10 seconds.

Discover Sophie Germain primes special prime numbers with unique properties. Learn about their relation to safe primes applications in cryptography and how to identify them using Python.

Prove the equality of cosine series in generalized functions. Learn how to manipulate trigonometric series for advanced applications.
Discover the surjective functions f(x) that satisfy the equation 2xf(f(x)) = f(x)(x + f(f(x))) for all positive real numbers x.

Discover how to find functions f(x) and g(x) that satisfy a specific functional equation. Explore different cases and solutions.

Discover how to find all surjective functions f:R→R satisfying a specific functional equation. Learn the key steps and techniques.

Struggling with functional equations for your math midterm? This post provides tips and tricks including substituting values using mathematical induction and finding fixed points to help you solve these challenging problems.

Determine the value of ‘a’ to ensure continuity of a piecewise function at x = 0 using limits and Taylor series.

Calculate the limit of cos(√x) raised to the power of 1/x as x approaches 0 from the right. Learn the Taylor expansion method for solving this type of limit problem.

Learn how to evaluate the limit of x^x as x approaches 0 from the positive side using logarithms and L’Hôpital’s rule. Find the answer!

Learn how to evaluate the limit of x times the natural log of (1 + 1/x) as x approaches infinity using L’Hôpital’s Rule.

Find the limit of a trigonometric expression as x approaches 0. Learn how to use trigonometric identities to solve this problem.

Learn how to add two vectors and find the magnitude and angle of the resultant vector. This guide provides a step-by-step explanation.
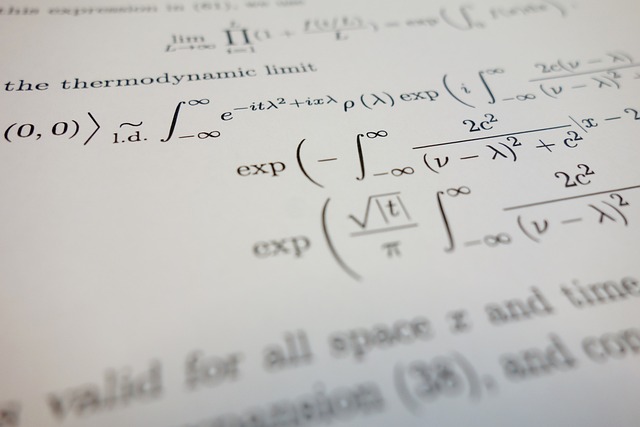
Learn about vectors in mathematics their properties and how they’re used in physics computer graphics and machine learning.
Proba-3 a cutting-edge Sun-observing satellite successfully launched from Sriharikota. The mission aims to advance space weather research.

Learn various methods for proving mathematical statements including direct proof indirect proof (contradiction and contrapositive) proof by cases and mathematical induction. Explore examples and applications.

Learn about just-in-time (JIT) compilation its benefits drawbacks and use cases in modern programming.

Conquer the CBSE Board Exams 2025 with our guide! Learn effective study strategies, time management tips, and overcome exam anxiety for success.

The additive inverse of an element, a fundamental concept in mathematics. Learn how to determine it and why it matters.

Explore the concept of Additive Identity in Mathematics and its importance in algebra and number theory.

What is probability? Probability is a fundamental concept in mathematics and statistics that deals with the likelihood of an event occurring. It is a way to quantify uncertainty and make predictions based on available information. In simple terms, probability is a...
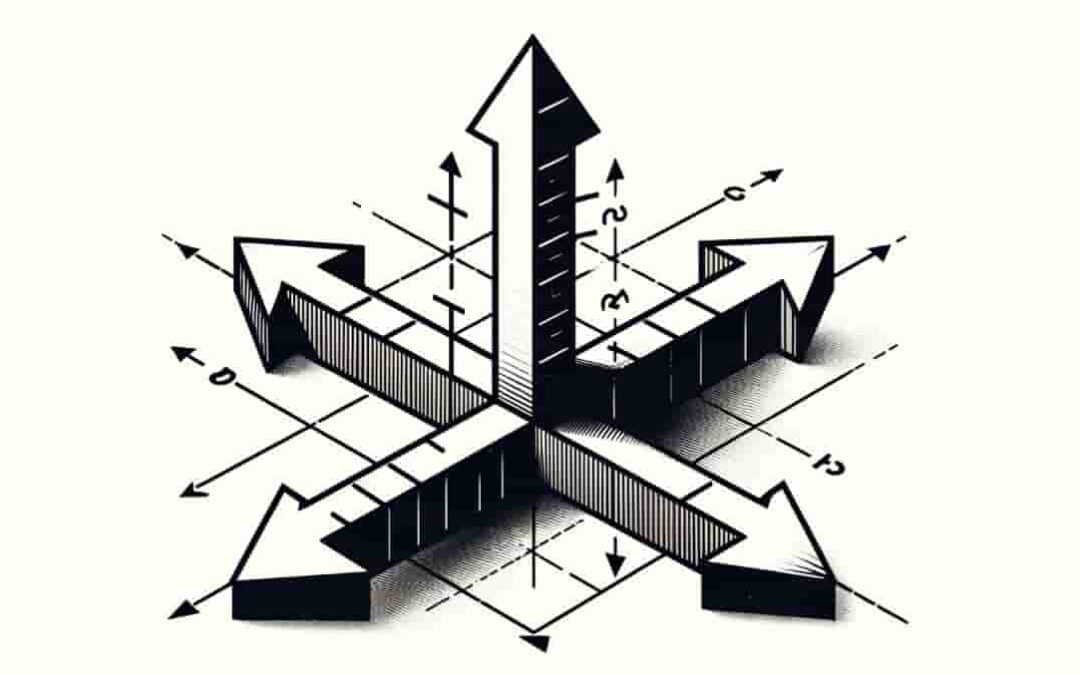
In physics and geometry, the concept of "three dimensions" refers to a spatial framework necessary to describe the position or location of an object fully. Each dimension provides a unique axis that, together with the others, can describe any point in space. Here’s a...

Scientific notation is a way to express very large or very small numbers in a compact form. It's especially useful in fields like science, engineering, and mathematics where such numbers frequently occur. The notation is based on powers of 10. Here's the general form:...

The multiplication rule in probability is used to find the probability of the intersection of two or more independent event

Addition Rule calculates the probability of one or more events occurring. For mutually exclusive events, add individual probabilities. For non-mutually exclusive events, add individual probabilities and subtract the probability of both events occurring.
Finding the Expected Value μ (mean) of Random Variable that has Poisson Distribution

In probability theory and statistics, λ (lambda) is a parameter used to represent the average rate or average number of events occurring in a fixed interval in the context of a Poisson distribution.

Derive the formula of Variance of the Poisson Distribution
uniformly distributed aerosol particles between 2 and 6 nanometers

Probability theory is a fascinating subject that has many applications in the real world. Understanding the basics of random variables and probability distributions is essential for anyone working in a field that deals with uncertainty. By mastering probability theory, you can make better decisions and improve your ability to analyze and interpret data.
Practical illustrations of Random Variables that we are exposed to in our daily life
The six trigonometric functions are defined below. Refer to the above diagram to get the relational picture. sinθ = \( \dfrac {\mathrm{perpendicular}} {\mathrm{hypotenuse}} = \dfrac {p}{h} \) cosθ = \( \dfrac {\mathrm{base}} {\mathrm{hypotenuse}} = \dfrac {b}{h}...
Pythagoras’ theorem is stated as : The sum of the areas of the two squares on the perpendicular(p) and base(b) of a right-angle triangle is equal to the area of the square on the hypotenuse(h). i.e. p2 + b2 = h2
A right-angle triangle is a triangle in which one of the angles measures 90°. Right-angled triangles have wide applications in mathematics and physics and as such, it became convenient to have specific names for their sides so that the problem statement in mathematics...
The trigonometric functions can be described on an x-y coordinate plane (Euclidean plane) using a circle of radius 1 unit and cutting a sector that subtends an angle θ at the centre. Refer to the diagram below for details.
By definition, L (length of arc) = ( \dfrac { \mathrm{θ_{deg} } } {360} ) × Circumference (arc length is proportional to angle, one complete arc subtends 360° at center) Also, Circumference = 2 ? r Hence, L = ( \dfrac { \mathrm{θ_{deg} } } {360} ) × 2 ? r ...
A number not divisible by 2 is called an odd number. Any number whose unit digit(last digit) is either 1,3,5,7 or 9 is an odd number. The set of all odd numbers is represented as Odd numbers = { 2n+1: n ∈ Z } where Z is the set of all integers. When an even...
A number divisible by 2 is called an even number. All numbers whose unit digit(last digit) is either 0,2,4,6 or 8 is an even numbers. The set of all even numbers is represented as follows: Even numbers = { 2n: n ∈ Z } where Z is the set of all integers. Zero is...
The cartesian product of two sets A and B is defined as a set formed by all the possible ordered pairs of elements from A and B, such that the first element comes from set A and the second element comes from set B. The cartesian product is denoted as A × B. Let a and...
An ordered pair is a 2-tuple formed by taking two elements (generally numbers but can be alphabets, characters, words or symbols). The general form of representation is (a, b) where a and b represent two distinct objects. The important thing with ordered pairs is that...
Tuples in Relations and their examples
A Relation from set A to set B is defined as a set of ordered pairs formed from the elements of set A and B. In other words, a relation is a subset of the cartesian product of sets A and B. The subset is derived by establishing predicate filter(s) or criteria stating...
A function is said to be an even function if the sign of the image does not change when the sign of the preimage changes. Conversely, a function is called an odd function when the sign of the image changes when the sign of the preimage changes. For Even functions,...
Question What does it mean for one event ? to cause another event ? - for example, smoking (?) to cause cancer (?)? There is a long history in philosophy, statistics, and the sciences of trying to clearly analyze the concept of a cause. One tradition says that causes...
Solution We have A = (1,4), (2,3), (3,2), (4,1) B = (1,4), (2,4), (3,4), (4,4), (5,4), (6,4), (4,1), (4,2), (4,3), (4,5), (4,6) \( P(A|B) = \dfrac {P(A∩B)}{P(B)} \) \( A∩B = (1,4), (4,1) \) The sample space comprises of 6×6 = 36 eventsHence,\( P(A∩B) = \dfrac{2}{36} =...
De Morgan’s First Law The complement of the union of two sets is equal to the intersection of their complements i.e. (A ∪ B )' = A' ∩ B' De Morgan’s Second Law The complement of the intersection of two sets is equal to the union of their complements i.e. (A ∩ B )’ =...
A cartesian product between two sets is defined as the set consisting of all possible ordered pairs that can be formed by taking one element from each of the sets at a given time. If A and B are two sets such that a ∈ A and b ∈ B, then the cartesian product between A...
In mathematics, a tuple or a sequence is a list of objects arranged in an order. Such a list may have repeated objects but the order is more important. Such sequences or tuples are denoted as ( t1, t2, t3, …., tn ) where tn is the nth element of the list. Below are a...
An ordered pair is a 2-tuple formed by taking two elements (generally numbers but can be alphabets, characters, words, or symbols). The general form of representation is (a, b) where a and b represent two distinct objects. The important thing with ordered pairs is...
The cartesian product of two sets A and B is defined as a set formed by all the possible ordered pairs of elements from A and B, such that the first element comes from set A and the second element comes from set B. The cartesian product is denoted as A × B....
The intersection of two sets A & B is defined as a set that contains only those members which are common to both A and B. The intersection operation is denoted by the symbol ∩. Remember, for two disjoint sets (sets having no common elements), the...
The union of two sets A & B is defined as a set that contains all the member elements of A and B. the union operation is denoted by the symbol ∪. One point to remember here is that the union of two or more sets always gives a set with distinct...
The complement of a set A (that is a subset of a universal set U) is defined as a set that contains all the member elements and all subsets of U that are not part of the set A. The complement of a set is denoted using the symbol ‘ or c. Hence, A’ =...
Venn diagrams are the pictorial or graphical representation of sets and the various relationships that exist between sets. The representation consists of a rectangular box representing the universal set(U). All sets that are in context are drawn as circles...
When working with sets, a reference superset that contains all the sets and their subsets in context (i.e. the sets which are currently under consideration) is called a universal set. It provides a base set from which all of the sets of interest can be...
Partitioning of a set is distributing the member elements of a set among a group of non-empty subsets in such a way that each member lies in only one of these subsets. ⇒ ∅ ( Empty Set ) cannot be the partition of any set. Examples ⇒ The set { 1, 2, 3 } can be...
Two sets A and B are called disjoint when they have no element in common (except the empty set ∅ }.
The set of all possible subsets of a set S is called the power set of S, written as P(S). Examples ⇒ The power set of { ‘a’ } is { ∅, {‘a’} }The power set of { 2, 3 } is { ∅, {2}, {3}, {2,3} }The power set of {1, 2, 3 } is { ∅, {1}, {2}, {3}, {1,2}, {1,3}, {2,3},...
If A is a subset of B but A ≠ B, then A is called the proper subset of B, and B is called the proper superset of A. This relationship is represented as below A ⊂ B ( A is a proper subset of A )B ⊃ A ( B is a proper superset of A ) Examples ⇒ {...
If there are two sets A & B such that every element of A is also in B, then A is called a subset of B. In other words, A is contained in B. B is called the superset of A. In the set theory, this relationship is depicted as below...
Two sets A and B are said to be equivalent(≡) if each element of A is also an element of B and each element of B is also an element of A. If elements are repetitive in one set, then it is not required for it to repeat in the other set for the two sets to be...
Two sets A and B are said to be equal(=) if they have the same elements. The elements may not be in the same order. If an element appears n times in one set, then it must also appear n times in the other set. Mathematically, two sets A and B are equal if For each...
A set that has a definite number of elements is called a finite set else it is called an Infinite set. ⇒ A null set is a finite set. ⇒ For finite set S, n(S) is a finite number. ⇒ The standard mathematical sets like N, Z, R, etc. are all...
A set that has exactly one member is called a singleton set. { 1 } , { ‘a’ } , { x3 | x ∈ N , 2 < x < 3 } are all singleton sets.
A set that does not have any members is called an empty set. ⇒ Such sets are represented as {} or using the symbol ∅ (derived from Φ) which has been explicitly developed to designate an empty set. ⇒ Sometimes { ∅ } is also...
The number of elements in a set is called cardinality. The cardinality of a set A is generally represented by |A| or n(A) meaning the number of elements in set A. Examples: The cardinality of the set { 1, 45, 2, 34 } is 4. The cardinality of...
The position of elements in a set does not change the value or the meaning of the set. The above statement signifies that { 1, 2, 3 } and { 1, 3, 2 } and { 2, 3, 1 } are all the same set. A set is primarily a collection and not a sequential representation of elements....
As defined earlier, a set is a collection or group of objects. These objects are called members of the Set. This relationship is represented by using the symbol ∈. The symbol ‘∈’ means “is a member of ” or “belongs to” or “is an element of”. The...
In mathematical terms, the members of sets are called elements. A set is represented by enlisting its member elements within curly brackets. There are three general conventions adopted for set representation – Roster, Ellipsis & Set-Builder form. Roster form...
What is a set? A Set is a collection of items. The collection can be either real-world objects or imaginary or theoretical entities. It can be a collection of numbers, alphabets, colors, countries’ names, etc.