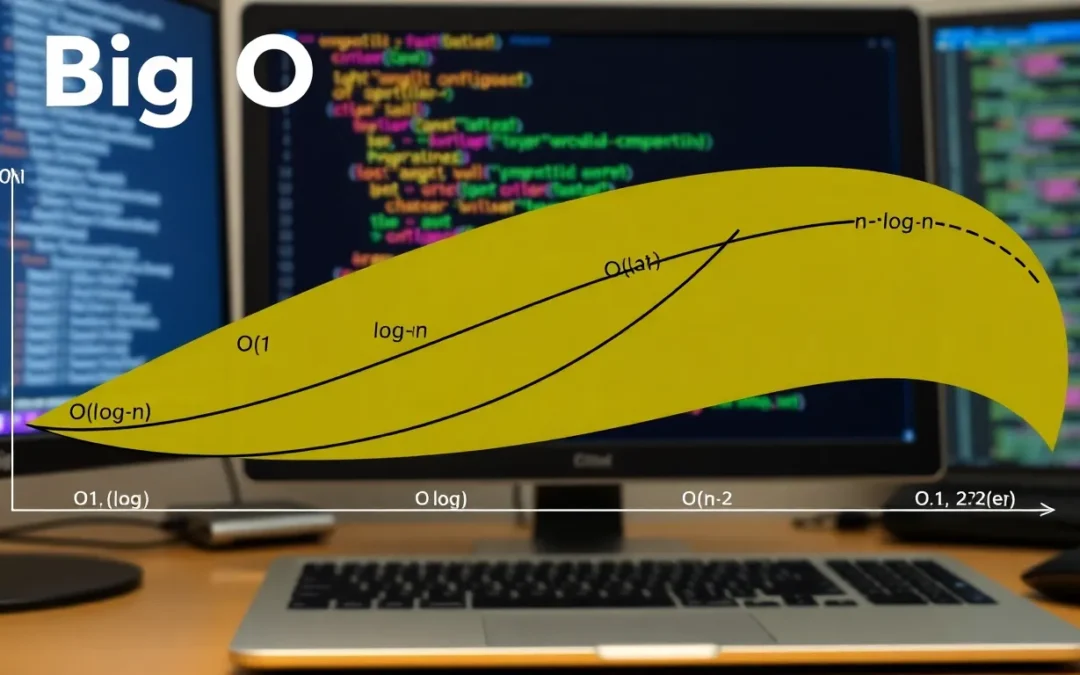
Big O notation is a crucial concept in computer science, describing the efficiency of algorithms. This guide offers a comprehensive overview of Big O notation and its applications.
ADVERTISEMENT

Big O notation is a crucial concept in computer science, describing the efficiency of algorithms. This guide offers a comprehensive overview of Big O notation and its applications.

Explore the fascinating world of the Banach Limit, a mathematical tool that extends the concept of limits beyond convergent sequences, assigning a limit value to sequences that might otherwise seem ‘limitless’.

A **Convergent Matrix** is a square matrix that converges to the zero matrix when raised to successive powers. This article explores the properties of these matrices and their importance in iterative methods.

Category theory limits provide a unified way to describe and relate various mathematical structures. This post explains how category theory limits are fundamental tools for understanding complex mathematical ideas.
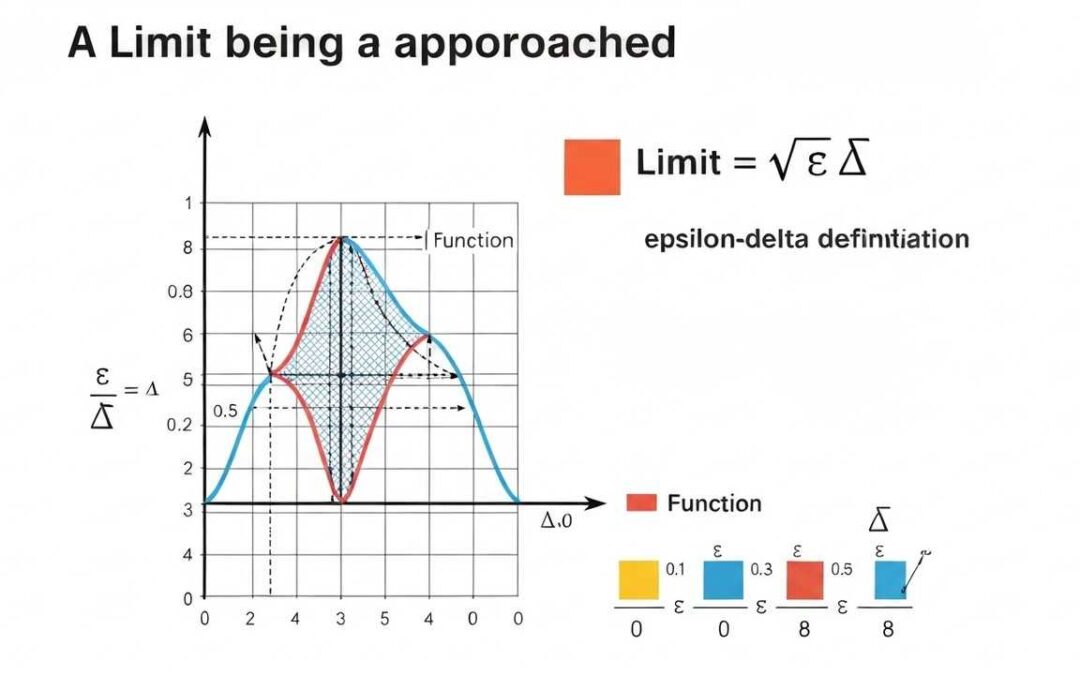
Understanding **limits of functions** is essential in calculus. This guide explains the epsilon-delta definition, theorems, and applications to help you master this fundamental concept.
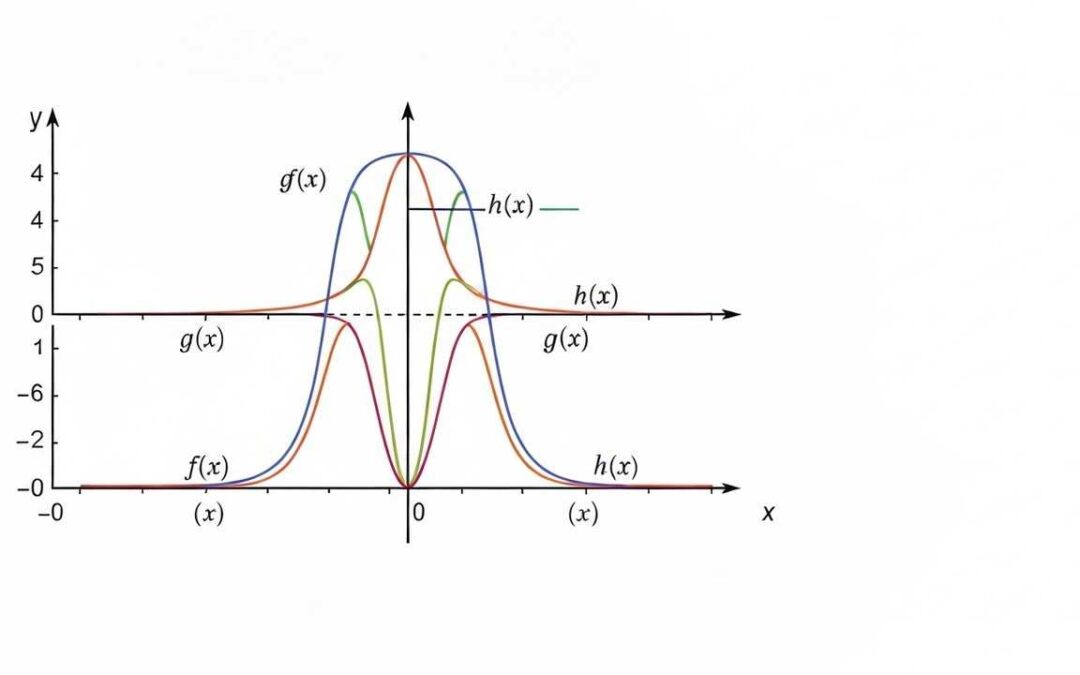
The Squeeze Theorem is a calculus concept that uses bounding functions to determine the limit of a function. The article explains how it works and provides examples.
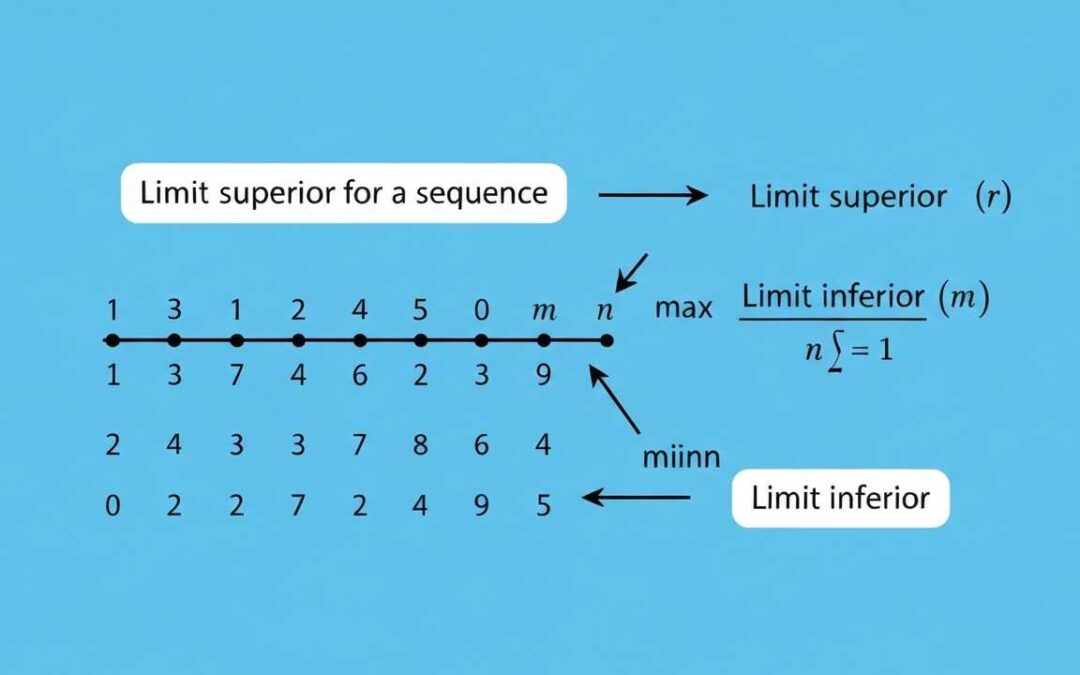
Understand Limit Superior and Inferior: Learn how these concepts define the eventual bounds of sequences and functions, and their importance in mathematical analysis.

Understanding the different **types of convergence** is essential in mathematics. From sequences and series to functions, this post explores the various modes of convergence.

Account for g=9.8 m/s² and the start-time offset.

Profit and loss questions improve real-world calculation ability.

Probability is key in logical and math aptitude exams.
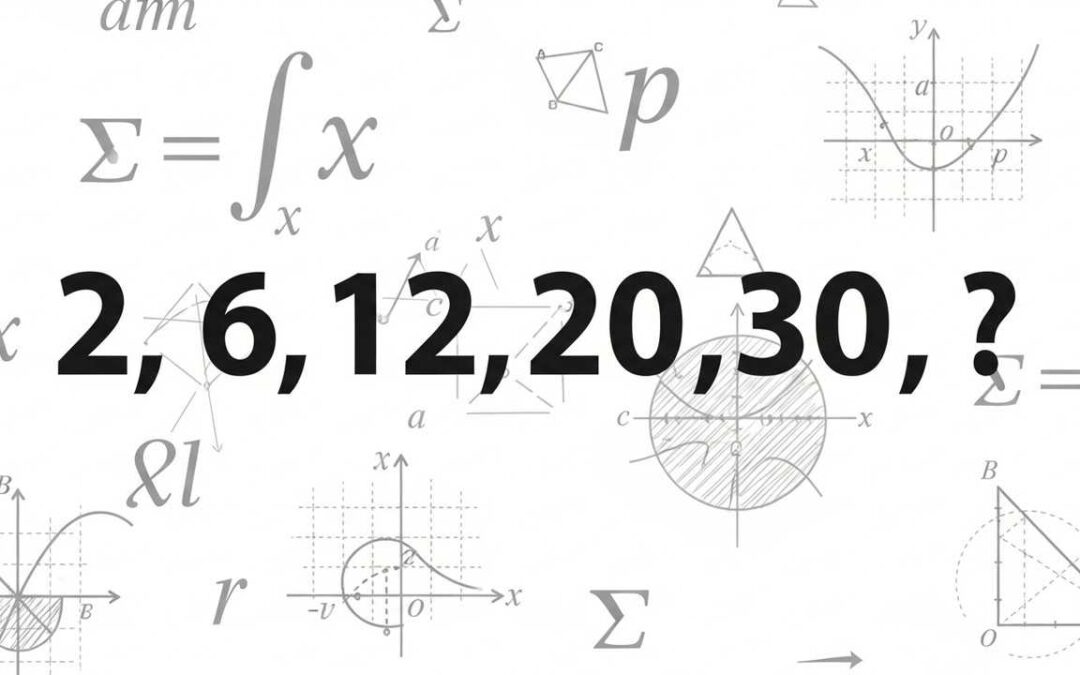
Number series problems improve pattern recognition for competitive exams.
Boost problem solving on cells.

Excel in electrostatics numericals.
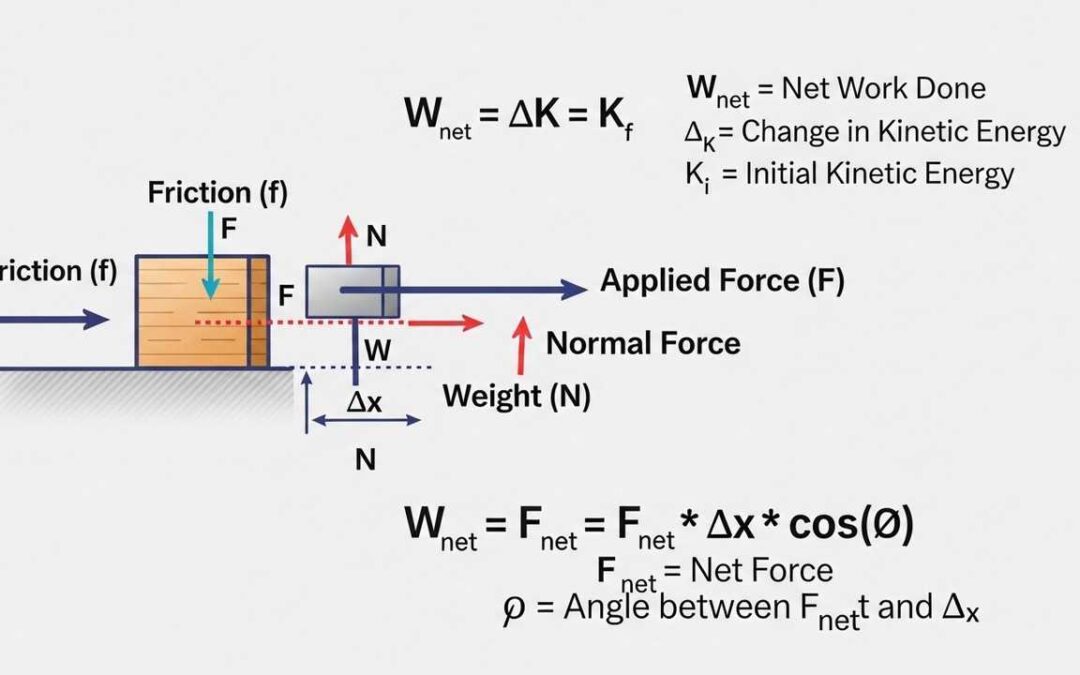
Strengthen energy-based problem solving.
Boost rotational mechanics problem solving.

Learn the basics! This post answers the question: What is a plane?
This post explores the Sum of Series Formula, showing you how to derive and apply it to solve complex series problems. You’ll learn the formula and see examples.
Learn how to solve trigonometric problems by understanding and applying Trigonometric Identities. We break down the steps to find ##\sin^3 \theta + \cos^3 \theta## when given ##\sin \theta + \cos \theta = \frac{5}{4}##.

Learn about **GCD calculation** and the Euclidean algorithm. This post provides a step-by-step guide to finding the greatest common divisor of two numbers, crucial in various mathematical applications.
Learn how to solve Evaluating Limits Problems with this step-by-step guide. We’ll cover the fundamentals and provide clear examples.

Learn how to calculate the Probability of Rolling a 7 with our easy-to-follow guide. Understand the step-by-step process and the math behind it.
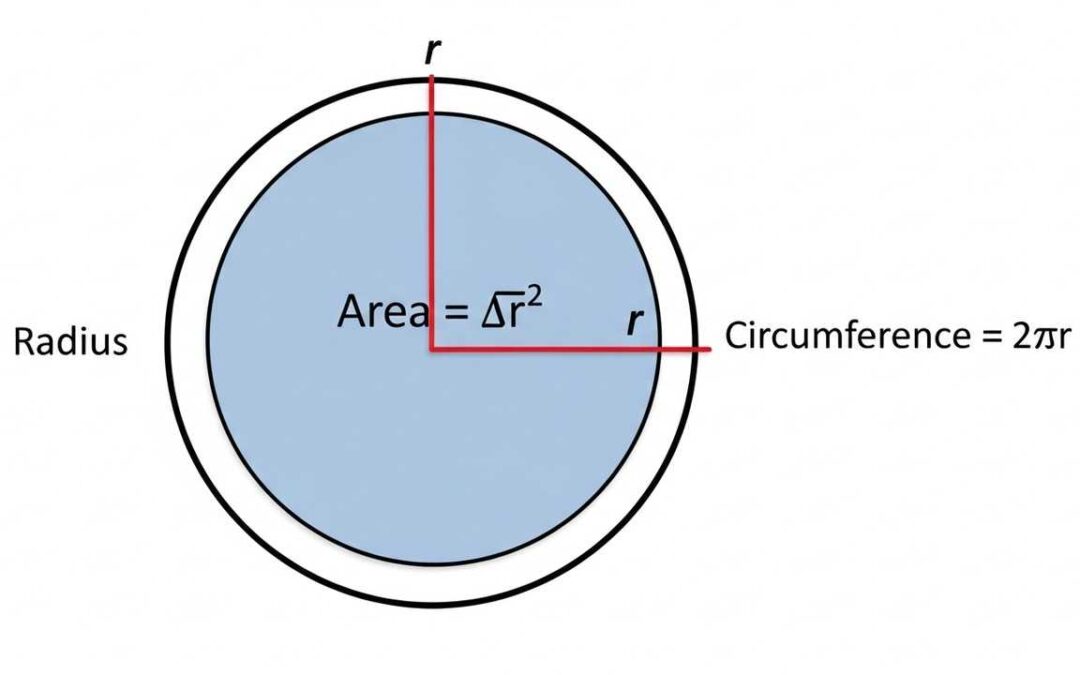
Learn how to calculate the **circle area and circumference** with a given radius using simple formulas and step-by-step examples. We’ll break down the process for easy understanding.

Learn how to **solve quadratic equations** using factoring and the quadratic formula. Discover the roots and understand the different methods with examples.

Learn how to solve Limits at Infinity with this comprehensive guide. Understand the concepts and techniques through clear examples and step-by-step solutions.

Learn how to solve Rationalizing Numerator Limits by rationalizing the numerator to eliminate indeterminate forms and find the limit.
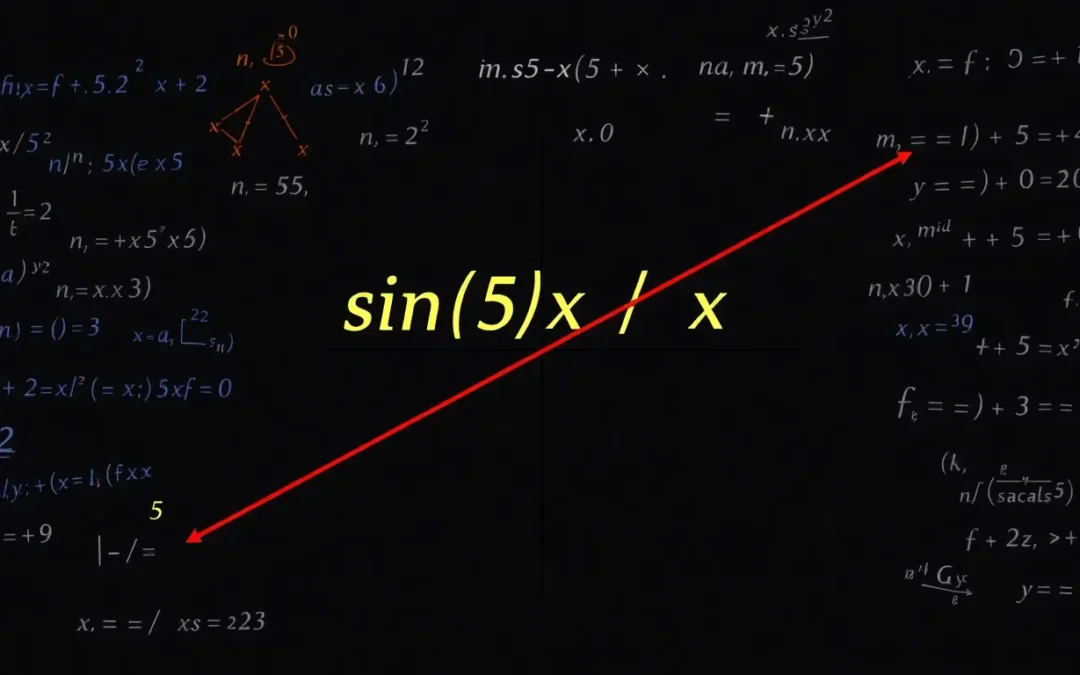
Learn to evaluate the Trigonometric Limit. The solution involves simplifying the expression and applying limit theorems. The final result is 5.
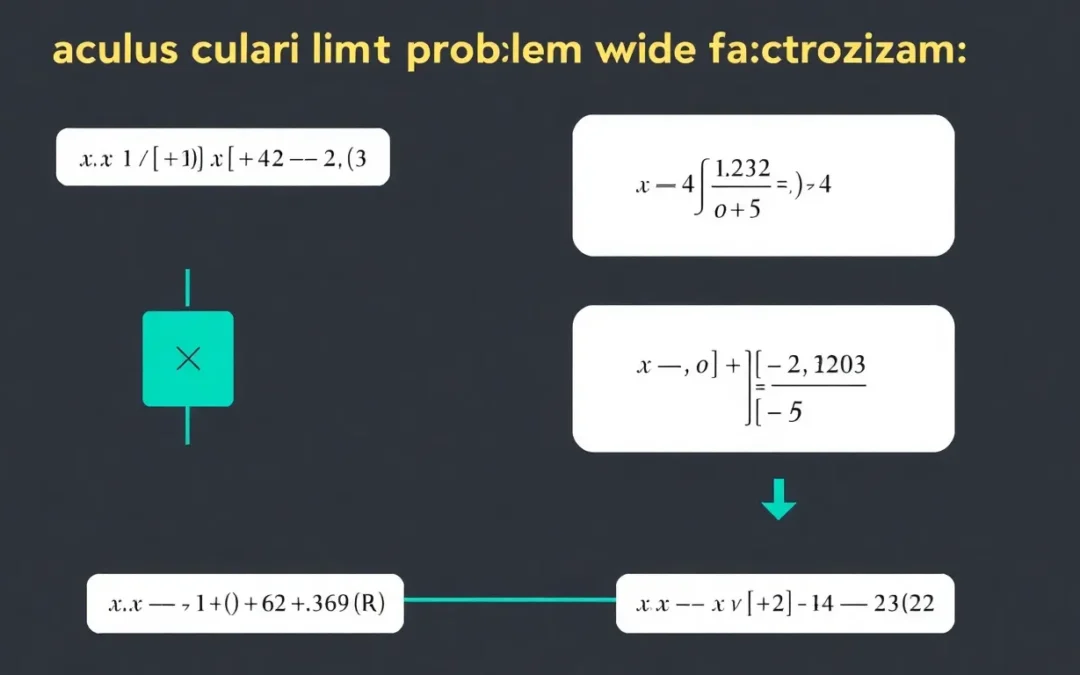
Learn to solve limits that result in indeterminate forms using **Limits by Factorization**. This method simplifies the expression to find the value the function approaches.
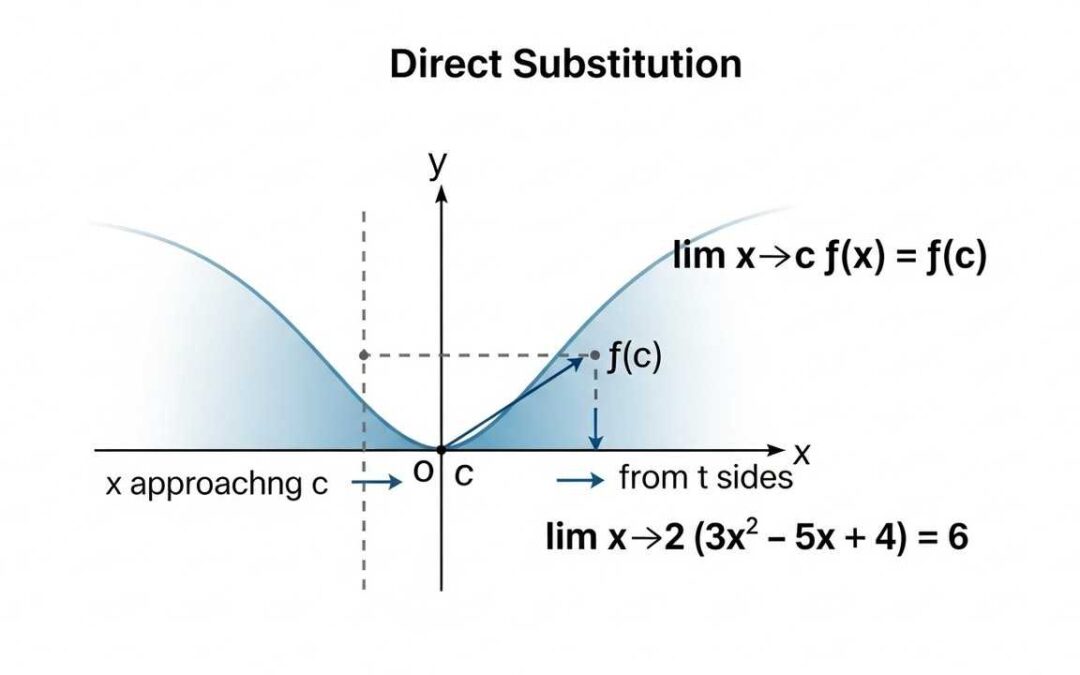
Learn how to easily evaluate limits using direct substitution! This guide provides clear examples and explanations to help you master this essential calculus skill. The SEO Keyphrase is Evaluating Limits.

Discover which functions have compositional square roots! Learn about bijections, cycle decomposition, and how to find these roots.

Understanding derivatives simply involves grasping how functions change. This guide offers an intuitive explanation for beginners.

Explore surjective function composition with clear examples. Learn when the composition of surjective functions remains surjective and when it doesn’t.

Explore the function codomain, its definition, and why it’s crucial in math. Understand its role in function composition and surjectivity.

Explore the conditions for defining integrals, focusing on the necessary structures of spaces and functions for meaningful integration.

Learn how to solve function composition problems algebraically with step-by-step solutions. Master the art of decomposing complex functions!

Understanding function notation is key! Learn the difference between f(x) and f, and how to use them correctly in math.

Explore the density of smooth functions in L1 and L2 spaces. Learn how smooth functions approximate complex functions effectively.

Learn how to tile piecewise functions diagonally across a grid. This guide provides a clear solution for transforming inputs and achieving the desired tiling effect.

Explore the definition, identification, and applications of prime numbers. Understand why prime numbers are crucial in cryptography and computer science.

Explore the probability of expected rolls to see all sides of a die. Understand why multiple dice don’t simply halve the expectation.

Learn about transformations in coordinate geometry. This guide provides a comprehensive explanation with illustrative examples.

Explore rotations and reflections in coordinate geometry with illustrative examples. Learn the fundamentals in simple language.

Explore the slope-intercept form to simplify linear equations effectively.

Explore the terms abscissa ordinate and applicate in coordinate geometry.

Explore the fundamental concept of a line in geometry. Learn the definition and key properties. What is a line?

Explore the fundamental concept: What is a point? Learn its definition and significance in various contexts.

Learn the basics of Euclidean geometry. This beginner’s guide explains key concepts in an easy-to-understand way.
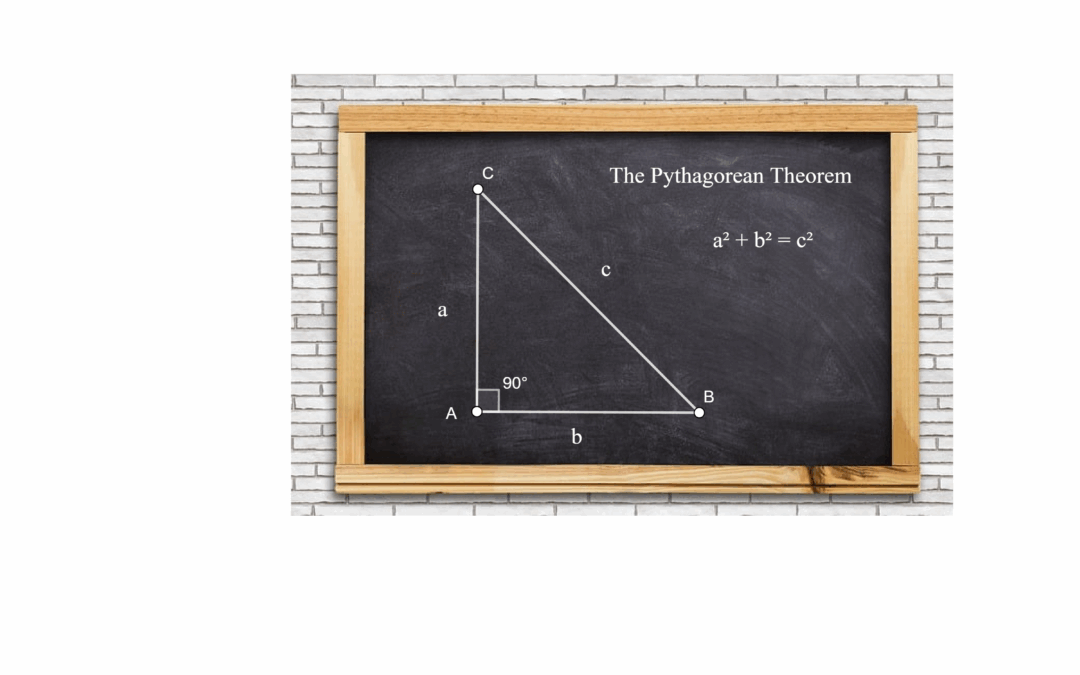
Learn the Pythagorean Theorem! Explore its history proof practical applications and solve 10 problems.

Learn about conic sections! This post explains ellipses parabolas hyperbolas and their properties in detail.
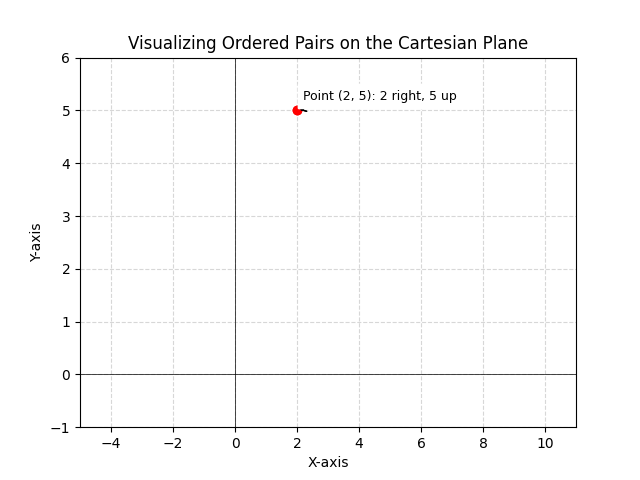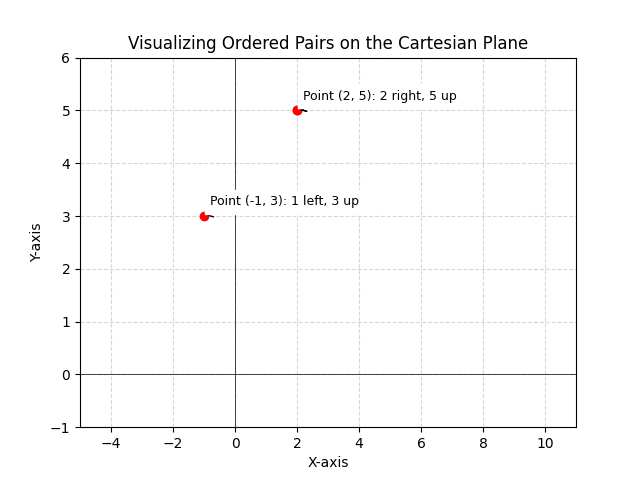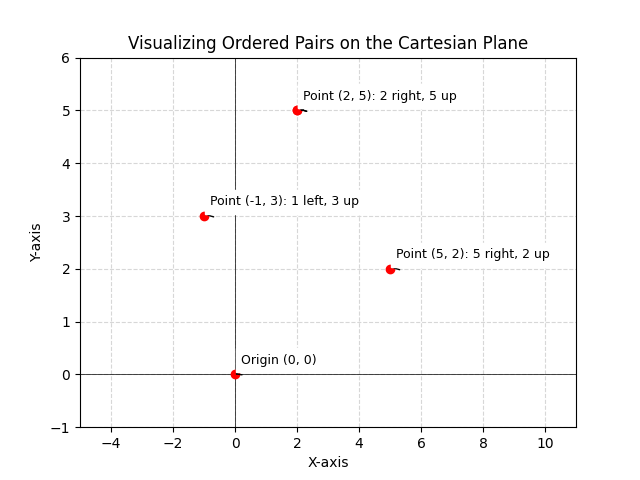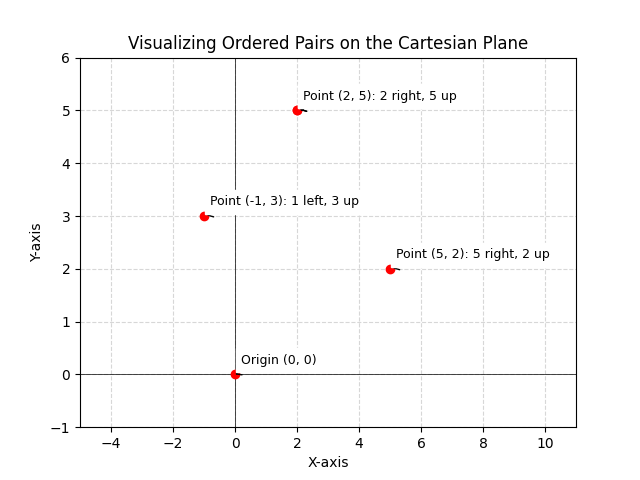
Learn the definition of an ordered pair in mathematics including its key characteristics and applications. Explore examples and understand how it’s used.

Learn about sequences their limits and how they differ from functions. Discover convergence and divergence and essential theorems.

Conquer the CBSE Board Exams 2025 with our guide! Learn effective study strategies, time management tips, and overcome exam anxiety for success.