In this post, We’re going to explore a fundamental concept in mathematics: What is a point? It might seem simple at first glance, but understanding the nature of a point is crucial for building a solid foundation in geometry and beyond. We’ll be looking at what defines a point, its properties, and why it’s so important in different mathematical contexts.

Furthermore, we’ll see how the idea of What is a point? has evolved over time, from the ancient Greeks to modern coordinate systems. We’ll discuss how mathematicians have defined and used points to create complex shapes and solve problems. This understanding is the cornerstone for grasping more advanced topics.

A point is the most basic geometric object, serving as the foundation for all other geometric figures. We’ll explore its definition, properties, and significance in various mathematical contexts, including Euclidean geometry and coordinate systems. Understanding the concept of a point definition is crucial for grasping more complex mathematical ideas.

---

---

What is a Point? – The Foundation of Geometry

In mathematics, particularly in geometry, a point is a fundamental concept. It is often described as a location in space that has no size, no width, no length, and no depth. It is a dimensionless entity, representing a specific position. Think of it as an infinitely small dot, a location that is perfectly defined but occupies no space. This abstract idea is the building block for all other geometric figures, such as lines, curves, surfaces, and solids. Without the concept of a point, we would lack the fundamental reference to construct any geometric shape or structure.

The definition of a point is axiomatic, meaning it is accepted without proof. We can’t “define” a point in terms of simpler concepts; instead, we describe its properties and how it relates to other geometric objects. A point is often represented by a dot and labeled with a capital letter, such as point A, point B, or point P. The position of a point can be described using coordinates in a coordinate system, allowing us to locate it precisely within a given space. For example, in a 2D Cartesian coordinate system, a point might be represented as (x, y), where x and y are numerical values indicating its horizontal and vertical position, respectively.

Properties and Characteristics of a Point

What is a point? – Properties of a Point

The key characteristic of a point is its lack of dimension. This means a point has no length, width, or thickness. It’s a zero-dimensional object. A point only defines a location. The concept of a point is abstract; it is a pure idea, not something that can be physically seen or touched. When we draw a dot to represent a point, we are only providing a visual representation, not the point itself. The dot has a size, but the mathematical point does not. This distinction is crucial for understanding geometric proofs and theorems. The point’s lack of dimension allows it to serve as the basis for constructing all other geometric figures.

What is a point? – Points in Different Dimensions

Points exist in spaces of various dimensions. In one dimension, a point can be located on a line. In two dimensions, a point can be located on a plane, and in three dimensions, a point can be located in space. The number of coordinates needed to define a point increases with the number of dimensions. For instance, in a 1D space (a line), a point is defined by a single coordinate (e.g., x = 3). In a 2D space (a plane), a point is defined by two coordinates (e.g., (2, 5)). In a 3D space, a point is defined by three coordinates (e.g., (1, 4, 7)). This concept extends to higher-dimensional spaces, although they are harder to visualize. Understanding how points behave in different dimensions is fundamental to many areas of mathematics, including linear algebra, calculus, and physics.

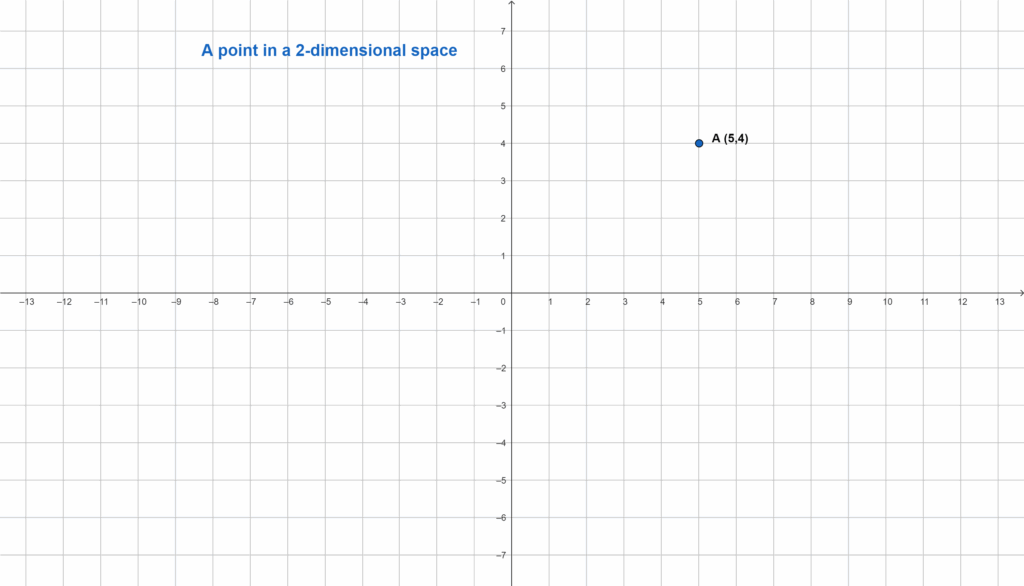
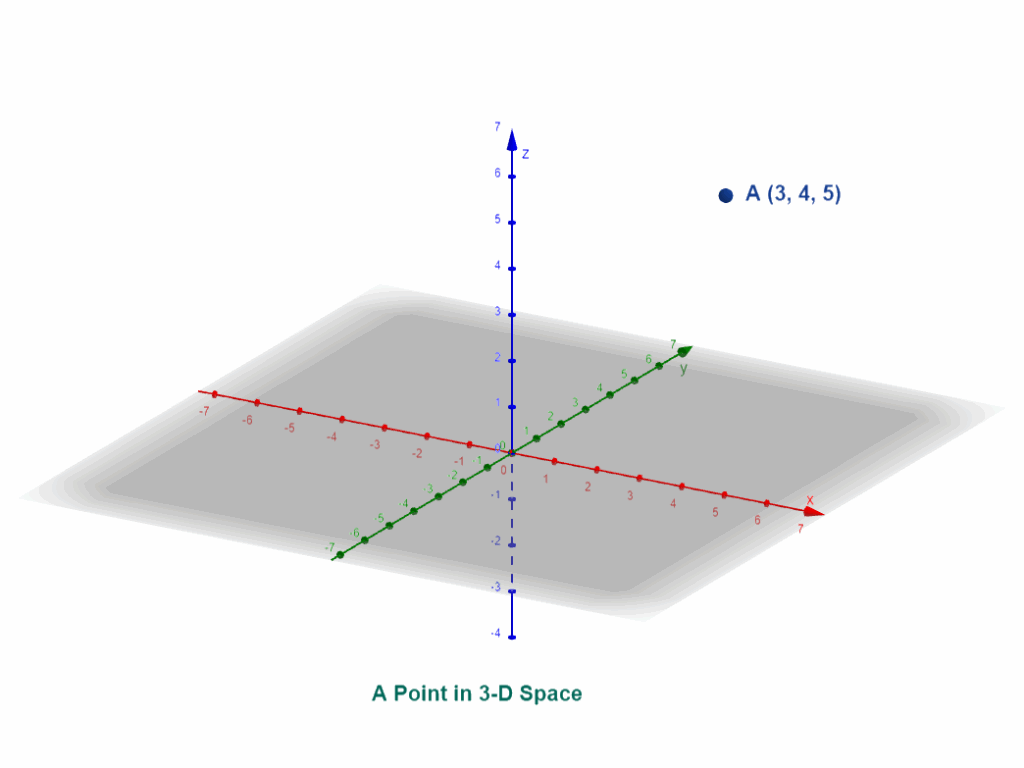
Historical Context and Significance

The concept of a point has a rich history, dating back to ancient Greek mathematicians like Euclid. In his “Elements,” Euclid laid the foundation for Euclidean geometry, defining a point as “that which has no part.” This definition, while seemingly simple, was revolutionary because it established a starting point for geometric reasoning. The concept of a point, along with other undefined terms like a line and a plane, formed the basis of his axiomatic system. This system allowed mathematicians to deduce complex geometric theorems from a set of fundamental assumptions.

The development of coordinate geometry by René Descartes in the 17th century further revolutionized the concept of a point. Descartes introduced the Cartesian coordinate system, which allowed points to be represented numerically using coordinates. This system provided a bridge between algebra and geometry, enabling mathematicians to solve geometric problems using algebraic methods and vice versa. The Cartesian coordinate system made it possible to define and analyze geometric shapes using equations, leading to significant advancements in calculus, physics, and engineering. The point definition became more concrete with the introduction of coordinates, allowing for precise calculations and visualizations.

Problems on Points

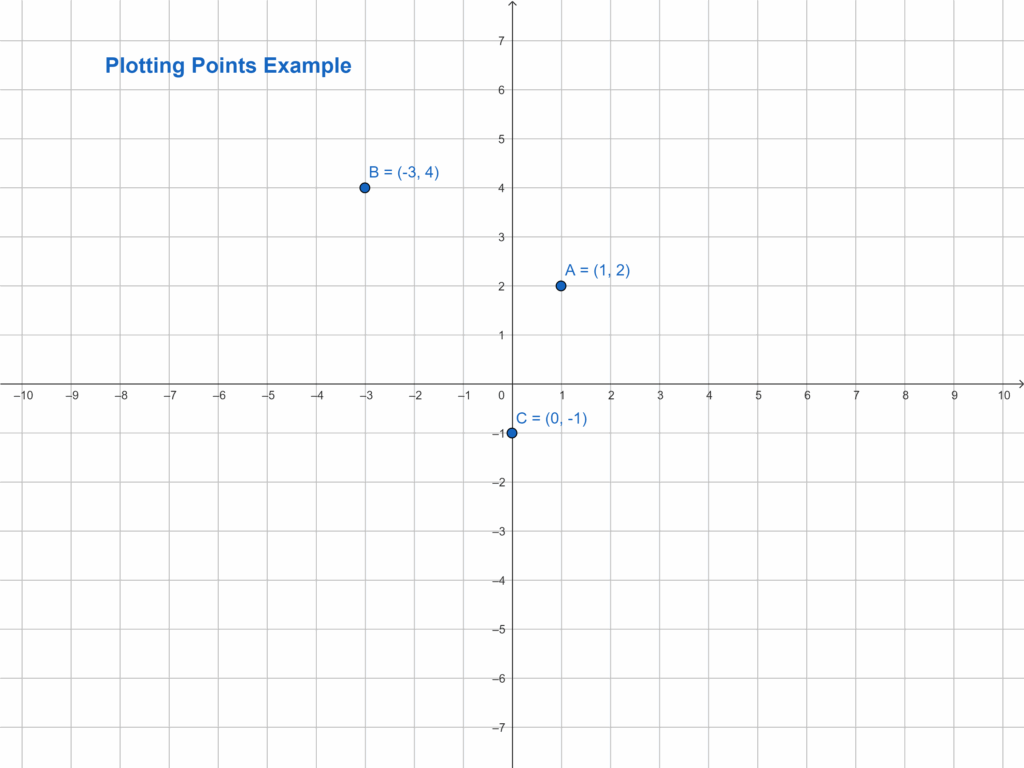
Problem 1: Plotting Points

Plot the following points on a 2D coordinate plane: A(1, 2), B(-3, 4), C(0, -1). This exercise reinforces the understanding of coordinate systems.

Solution: Plot each point according to its x and y coordinates.

Problem 2: Distance Formula

Calculate the distance between points A(1, 2) and B(4, 6) using the distance formula: ##d = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2}##. This problem uses the concept of points to calculate distances.

Solution: ##d = \sqrt{(4-1)^2 + (6-2)^2} = \sqrt{3^2 + 4^2} = \sqrt{25} = 5##.

Problem 3: Midpoint Formula

Find the midpoint of the line segment connecting points A(1, 2) and B(4, 6) using the midpoint formula: ##M = (\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2})##. This exercise applies the concept of points to find the middle of a line segment.

Solution: ##M = (\frac{1+4}{2}, \frac{2+6}{2}) = (2.5, 4)##.

Problem 4: Points in 3D Space

Describe the position of the point (2, -1, 3) in a 3D coordinate system. This problem tests the understanding of points in 3D space.

Solution: The point is located 2 units along the x-axis, -1 unit along the y-axis, and 3 units along the z-axis.

Problem 5: Collinear Points

Determine if the points A(1, 1), B(2, 3), and C(3, 5) are collinear. This problem involves the concept of points lying on the same line.

Solution: The points are not collinear because the slope between A and B is different from the slope between B and C.

---

---