A technical overview and step-by-step solution to the Atwood machine problem involving connected bodies in tension with masses of 4kg and 6kg.
Featured Articles on: LIMITS
Big O Notation: A Guide to Understanding Algorithm Efficiency
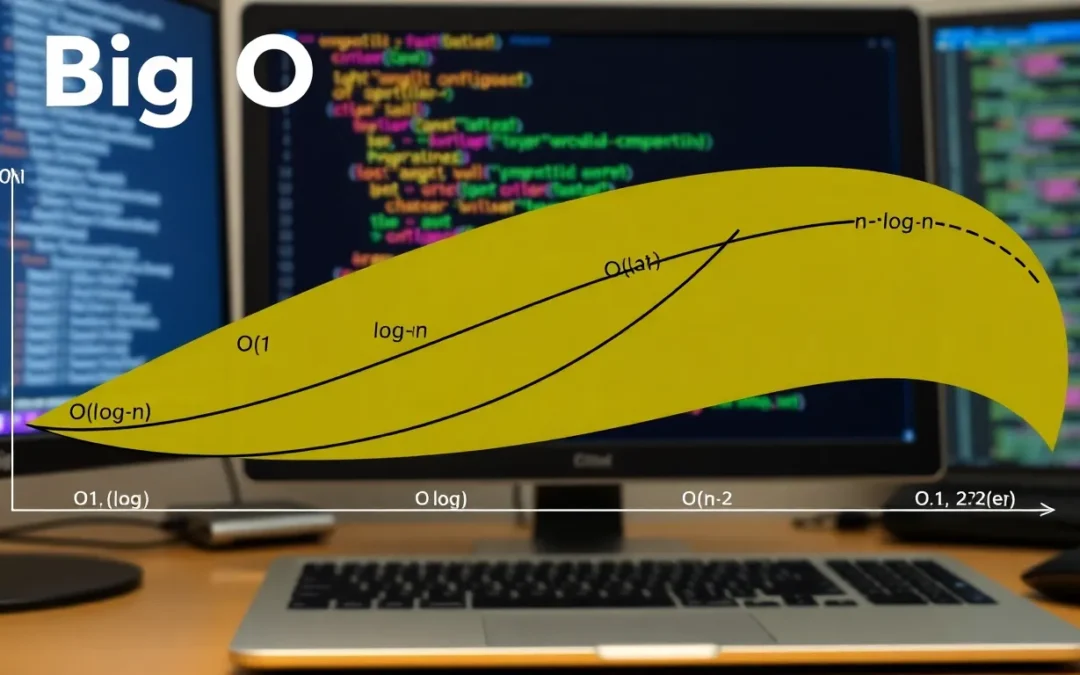
Big O notation is a crucial concept in computer science, describing the efficiency of algorithms. This guide offers a comprehensive overview of Big O notation and its applications.
The Power of Banach Limits
Explore the fascinating world of the Banach Limit, a mathematical tool that extends the concept of limits beyond convergent sequences, assigning a limit value to sequences that might otherwise seem ‘limitless’.
Understanding Stochastic Convergence
Explore the intricacies of Stochastic convergence, a vital concept in probability theory. Learn about the different types and their applications in statistics and stochastic processes.
Category Theory Limits
Category theory limits provide a unified way to describe and relate various mathematical structures. This post explains how category theory limits are fundamental tools for understanding complex mathematical ideas.
Limits of Functions: A Complete Guide
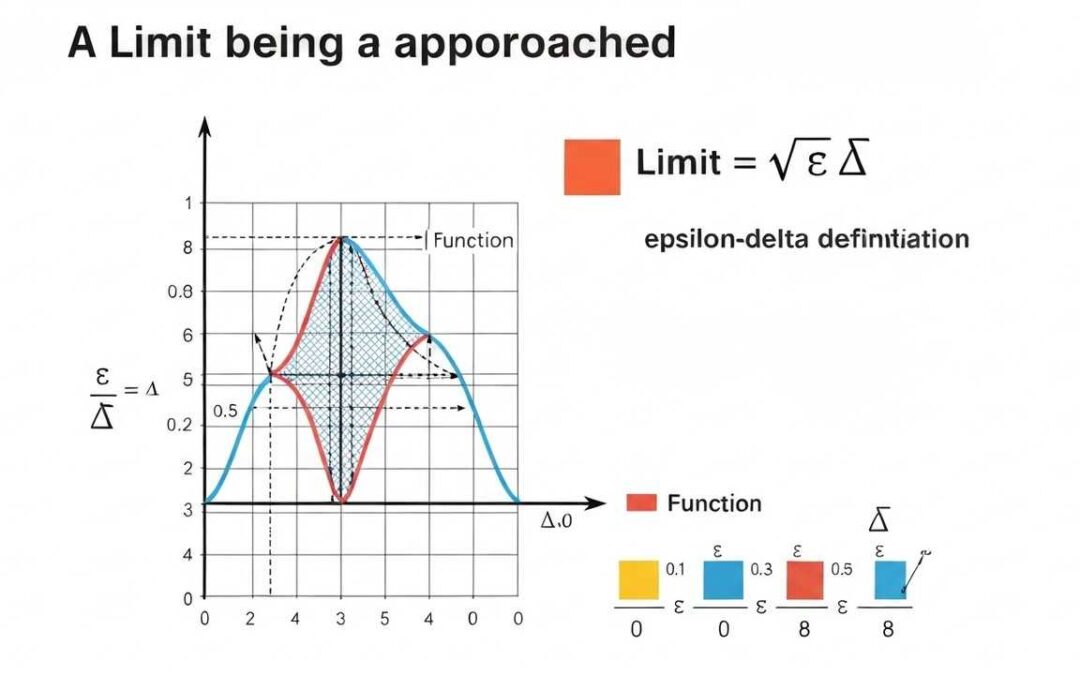
Understanding **limits of functions** is essential in calculus. This guide explains the epsilon-delta definition, theorems, and applications to help you master this fundamental concept.
Limits: The Squeeze Theorem Explained
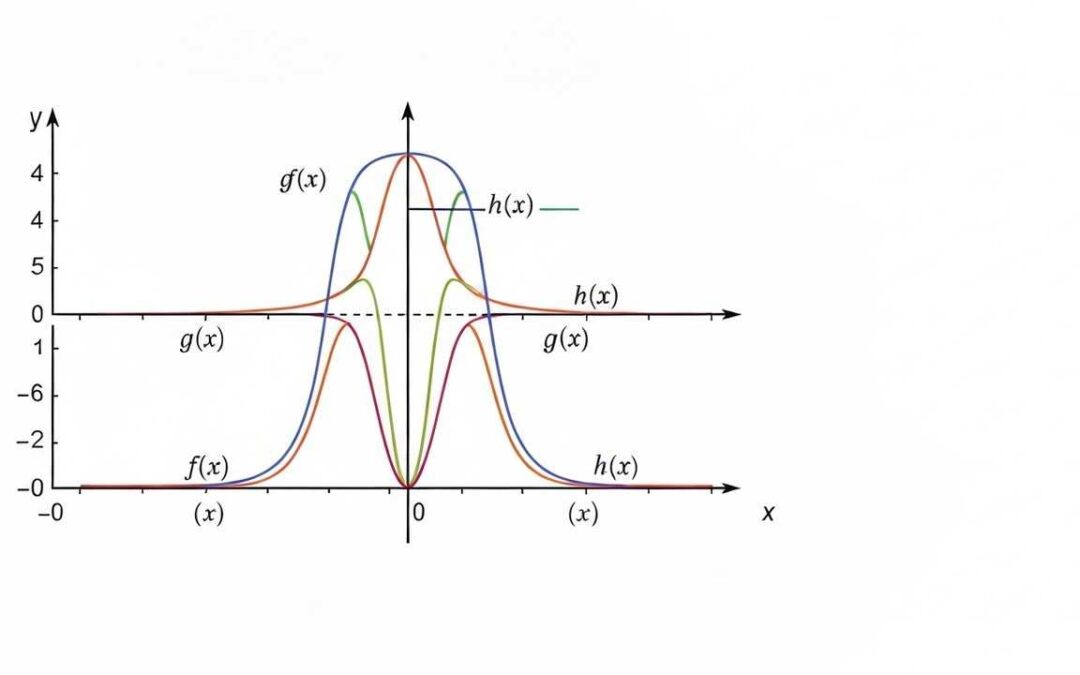
The Squeeze Theorem is a calculus concept that uses bounding functions to determine the limit of a function. The article explains how it works and provides examples.
Limit Superior and Inferior
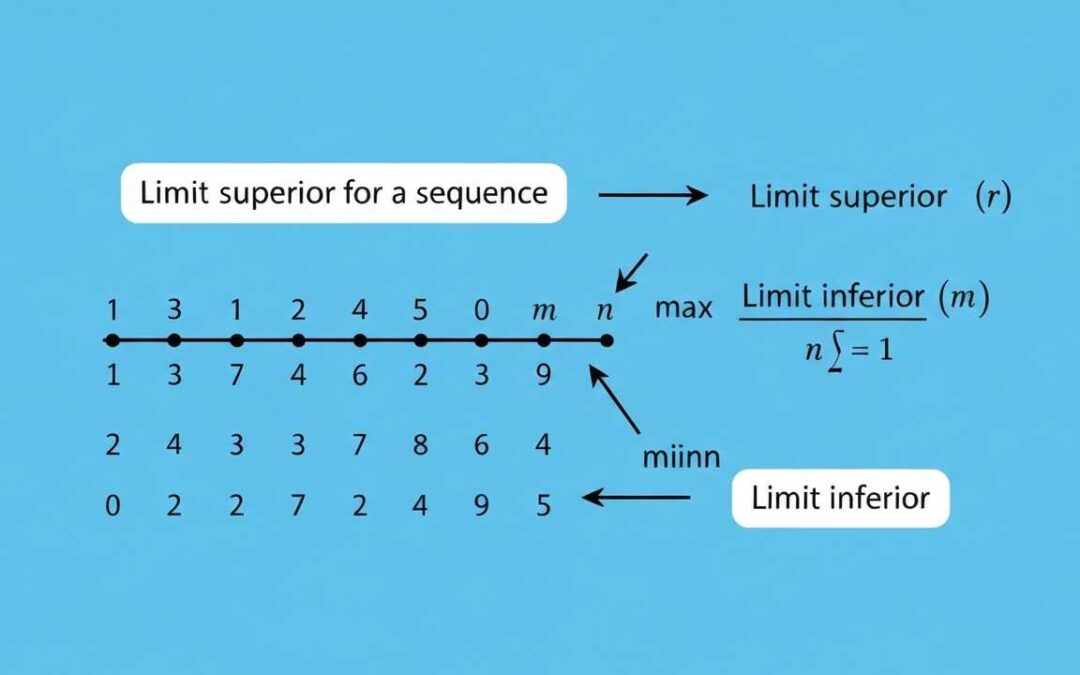
Understand Limit Superior and Inferior: Learn how these concepts define the eventual bounds of sequences and functions, and their importance in mathematical analysis.
The Diverse Types of Convergence in Mathematics
Understanding the different **types of convergence** is essential in mathematics. From sequences and series to functions, this post explores the various modes of convergence.
Evaluating Limits Problems: Step-by-Step Solutions
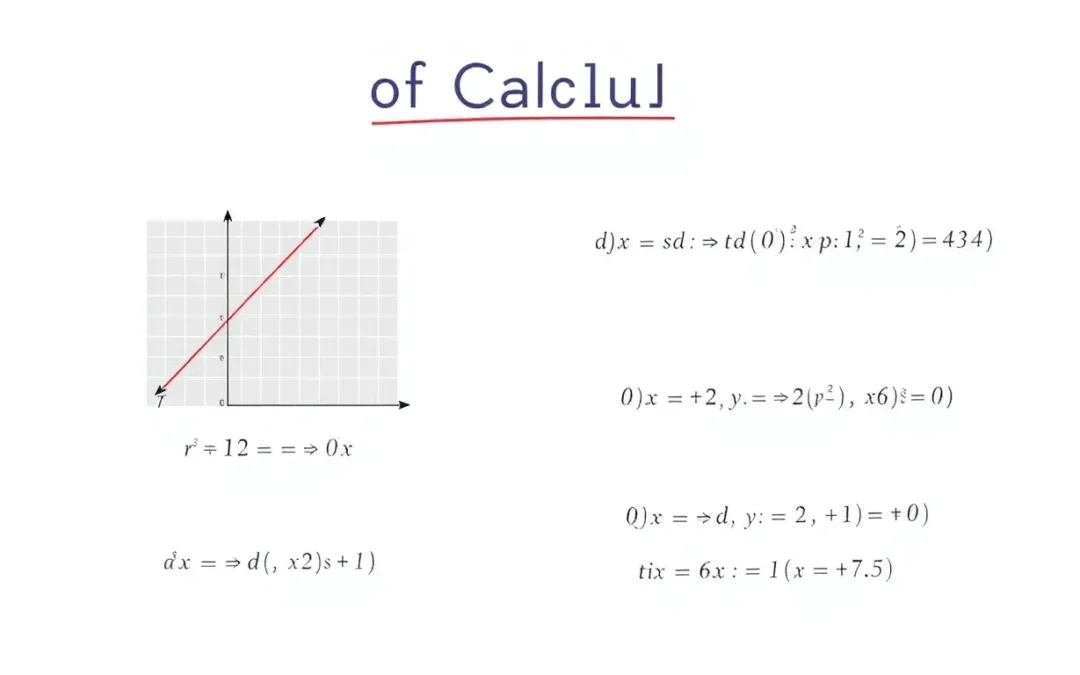
Learn how to solve Evaluating Limits Problems with this step-by-step guide. We’ll cover the fundamentals and provide clear examples.
Limits at Infinity
Learn how to solve Limits at Infinity with this comprehensive guide. Understand the concepts and techniques through clear examples and step-by-step solutions.
Rationalizing Numerator Limits
Learn how to solve Rationalizing Numerator Limits by rationalizing the numerator to eliminate indeterminate forms and find the limit.
Trigonometric Limit
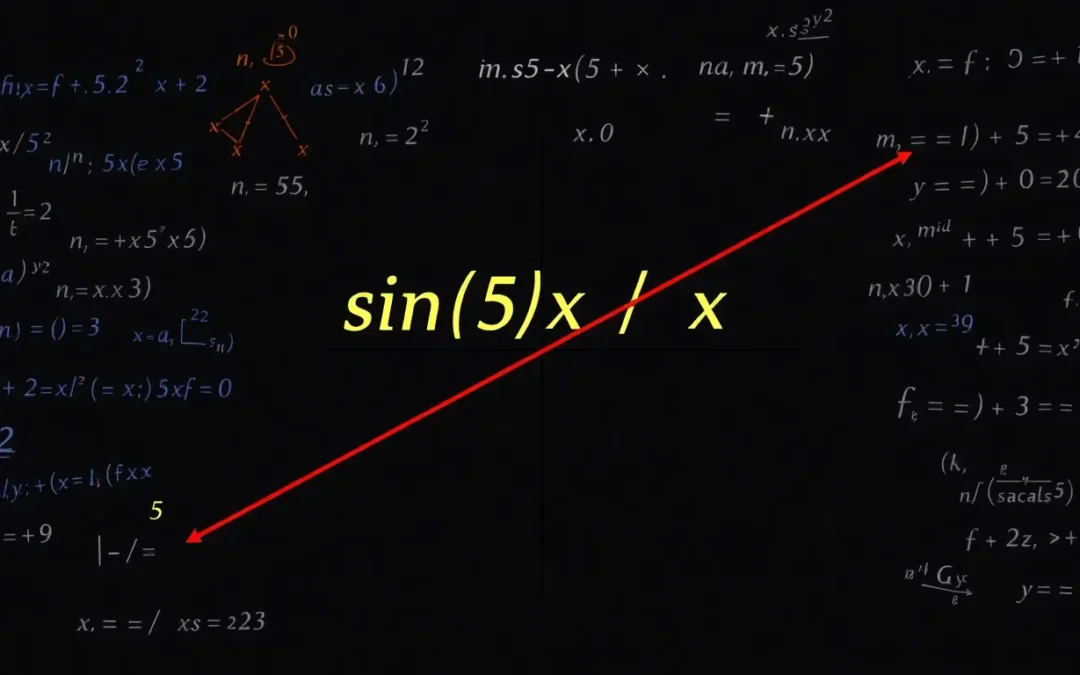
Learn to evaluate the Trigonometric Limit. The solution involves simplifying the expression and applying limit theorems. The final result is 5.
Understanding Limits by Factorization
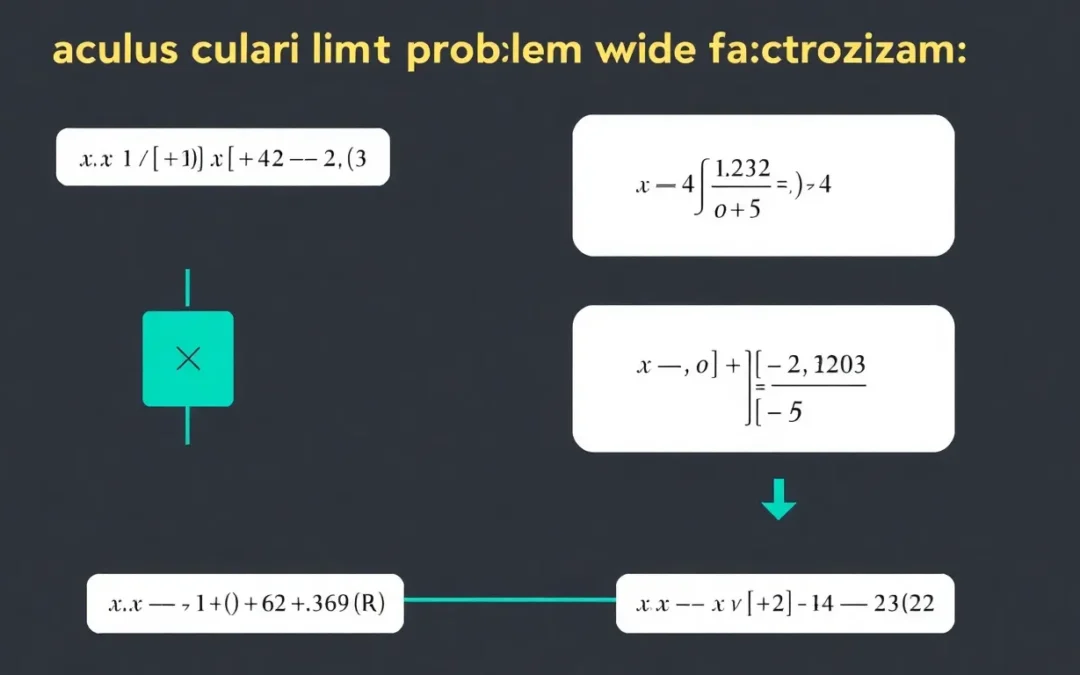
Learn to solve limits that result in indeterminate forms using **Limits by Factorization**. This method simplifies the expression to find the value the function approaches.
Evaluating Limits
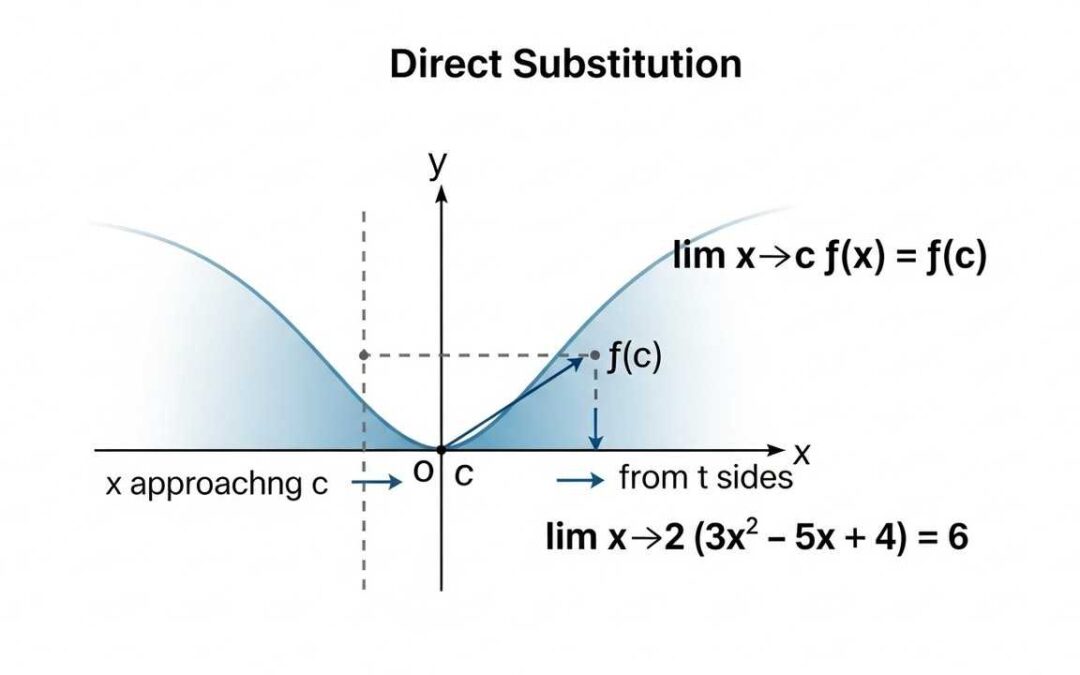
Learn how to easily evaluate limits using direct substitution! This guide provides clear examples and explanations to help you master this essential calculus skill. The SEO Keyphrase is Evaluating Limits.
Unpredictable Function Behavior: Exploring Large Variables
Explore how function behavior changes with large variables. Learn to identify warning signs and avoid common pitfalls in mathematical analysis.