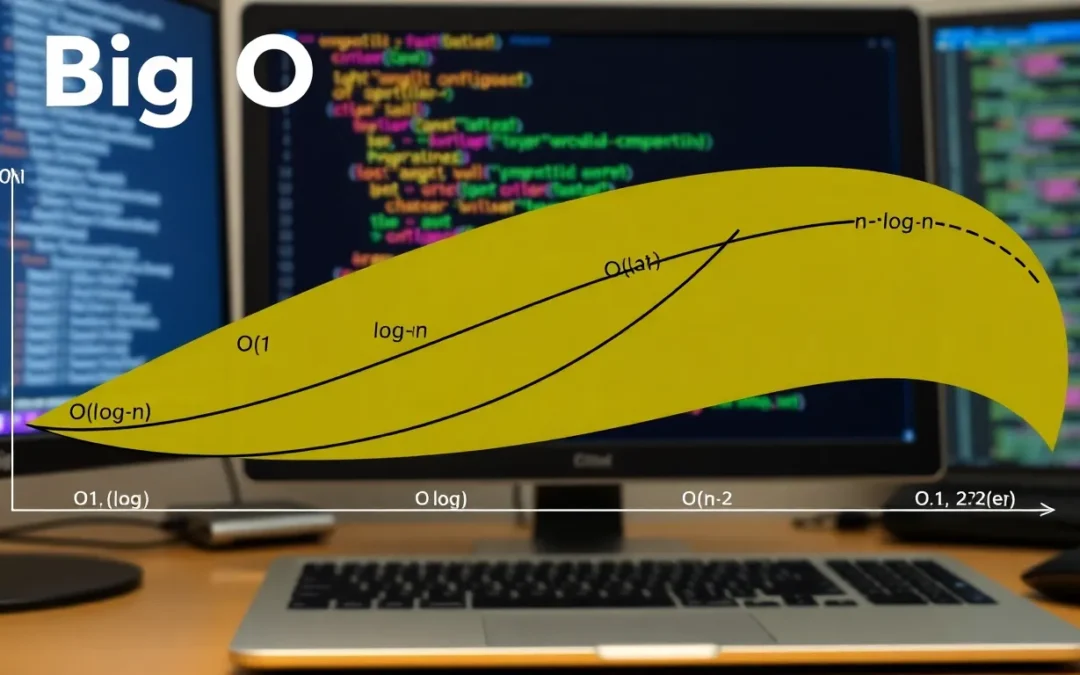
Big O notation is a crucial concept in computer science, describing the efficiency of algorithms. This guide offers a comprehensive overview of Big O notation and its applications.
ADVERTISEMENT

Big O notation is a crucial concept in computer science, describing the efficiency of algorithms. This guide offers a comprehensive overview of Big O notation and its applications.

Explore the fascinating world of the Banach Limit, a mathematical tool that extends the concept of limits beyond convergent sequences, assigning a limit value to sequences that might otherwise seem ‘limitless’.

A **Convergent Matrix** is a square matrix that converges to the zero matrix when raised to successive powers. This article explores the properties of these matrices and their importance in iterative methods.

Category theory limits provide a unified way to describe and relate various mathematical structures. This post explains how category theory limits are fundamental tools for understanding complex mathematical ideas.
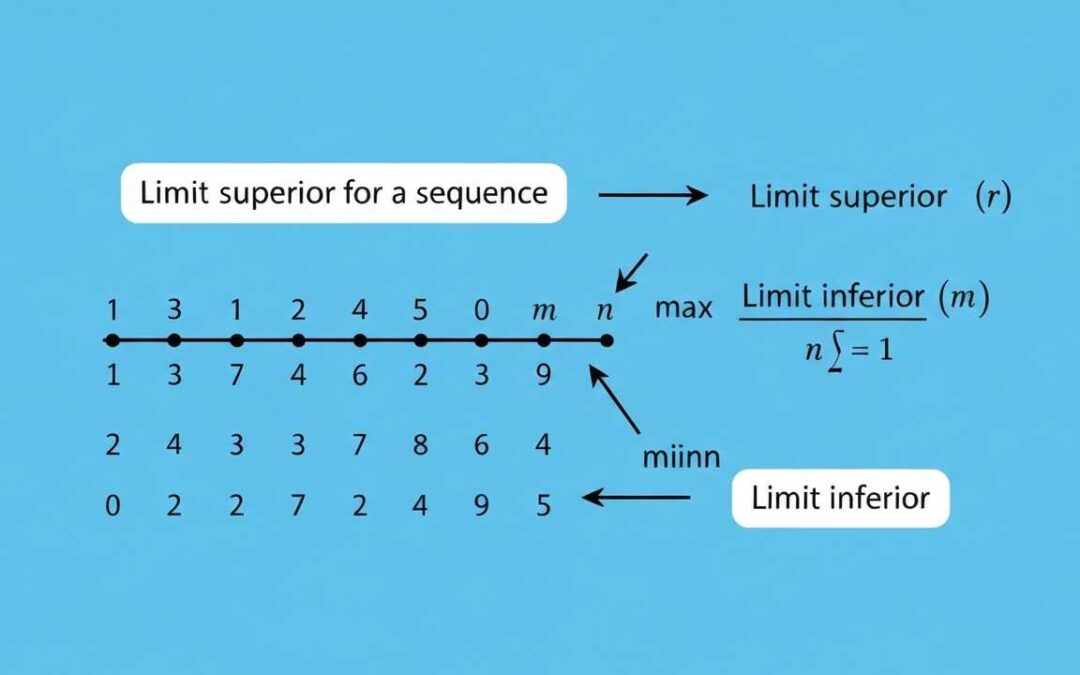
Understand Limit Superior and Inferior: Learn how these concepts define the eventual bounds of sequences and functions, and their importance in mathematical analysis.

Understanding the different **types of convergence** is essential in mathematics. From sequences and series to functions, this post explores the various modes of convergence.

Profit and loss questions improve real-world calculation ability.

Probability is key in logical and math aptitude exams.
This post explores the Sum of Series Formula, showing you how to derive and apply it to solve complex series problems. You’ll learn the formula and see examples.
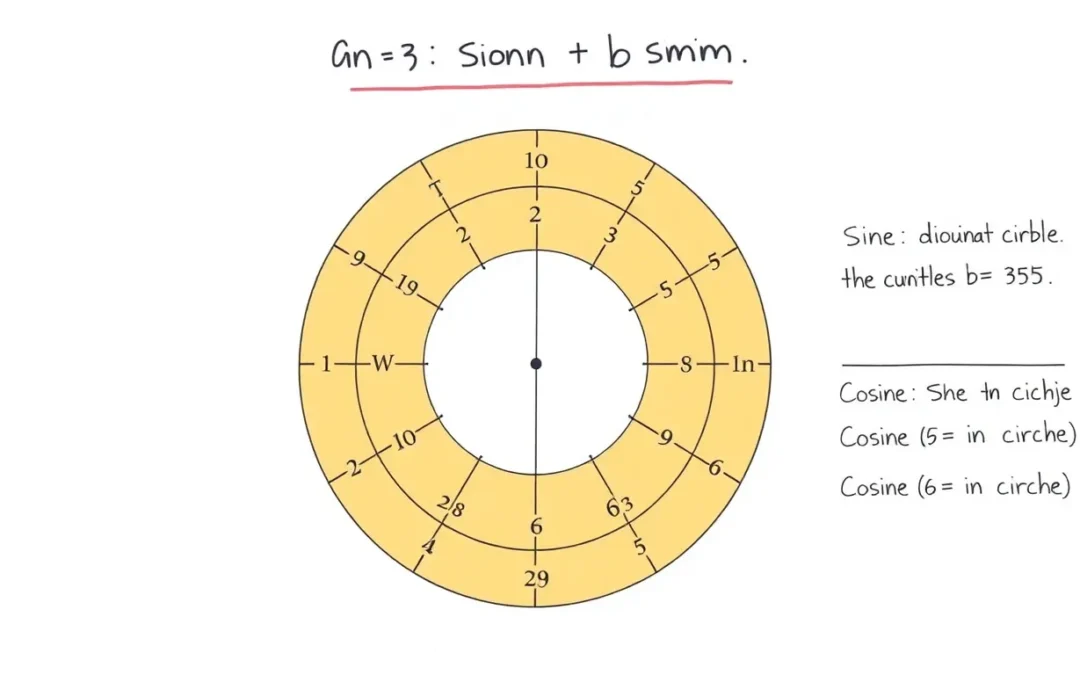
Learn how to solve trigonometric problems by understanding and applying Trigonometric Identities. We break down the steps to find ##\sin^3 \theta + \cos^3 \theta## when given ##\sin \theta + \cos \theta = \frac{5}{4}##.

Learn about **GCD calculation** and the Euclidean algorithm. This post provides a step-by-step guide to finding the greatest common divisor of two numbers, crucial in various mathematical applications.
Learn how to solve Evaluating Limits Problems with this step-by-step guide. We’ll cover the fundamentals and provide clear examples.

Learn how to calculate the Probability of Rolling a 7 with our easy-to-follow guide. Understand the step-by-step process and the math behind it.

Learn how to **solve quadratic equations** using factoring and the quadratic formula. Discover the roots and understand the different methods with examples.

Learn how to solve Limits at Infinity with this comprehensive guide. Understand the concepts and techniques through clear examples and step-by-step solutions.

Learn how to solve Rationalizing Numerator Limits by rationalizing the numerator to eliminate indeterminate forms and find the limit.
Learn to evaluate the Trigonometric Limit. The solution involves simplifying the expression and applying limit theorems. The final result is 5.
Learn to solve limits that result in indeterminate forms using **Limits by Factorization**. This method simplifies the expression to find the value the function approaches.

Discover which functions have compositional square roots! Learn about bijections, cycle decomposition, and how to find these roots.

Explore the divisibility by floor square root problem. Find all integers ##n## where ##\lfloor{\sqrt{n}}\rfloor \mid n##. Solutions and examples included.

Learn fuzzy logic aggregation techniques to combine uncertain data. Enhance decision-making and risk assessment with fuzzy values.

Learn how to perform function decomposition by separating any function into its even and odd parts, simplifying complex analysis.

Prove that an expression is independent of n using number theory. Explore modular arithmetic and floor functions to show constant results.

Explore L-structures in first-order logic, their construction, and counting methods. Understand how L-structures first order logic works with examples.

Learn how to solve function composition problems algebraically with step-by-step solutions. Master the art of decomposing complex functions!

Learn how to represent logical operators like AND, OR, and NOT as functions. Understand their mathematical formulations and applications.

Explore proving that the floor function has Theta complexity of Θ(x). Learn about upper and lower bounds in this analysis.
Learn how to efficiently compute the sum of coefficients in the Hadamard product of generating functions. Simplify complex calculations!

Explore generalized cosine functions through functional equations. Understand solutions and challenges in higher-order generalizations.

Learn how to tile piecewise functions diagonally across a grid. This guide provides a clear solution for transforming inputs and achieving the desired tiling effect.

Explore the definition, identification, and applications of prime numbers. Understand why prime numbers are crucial in cryptography and computer science.
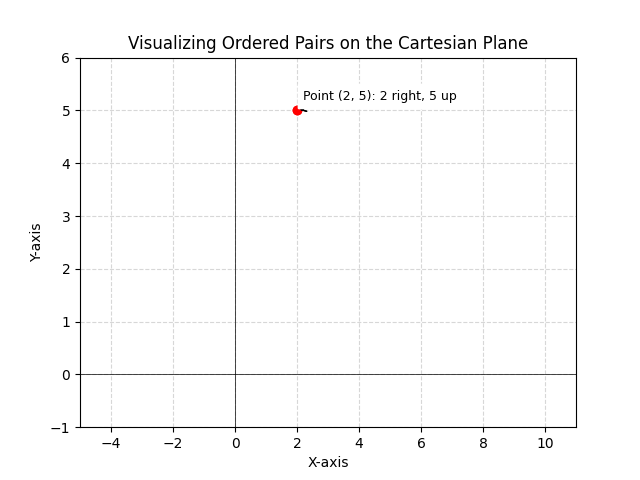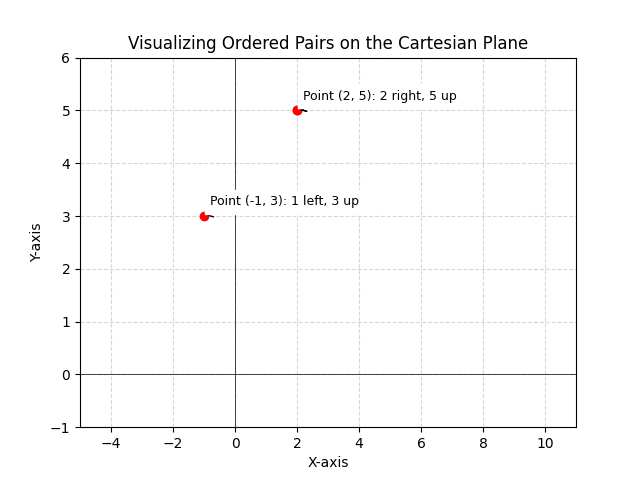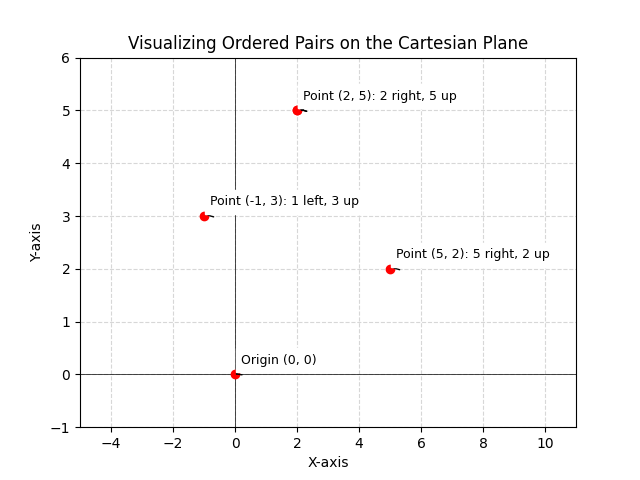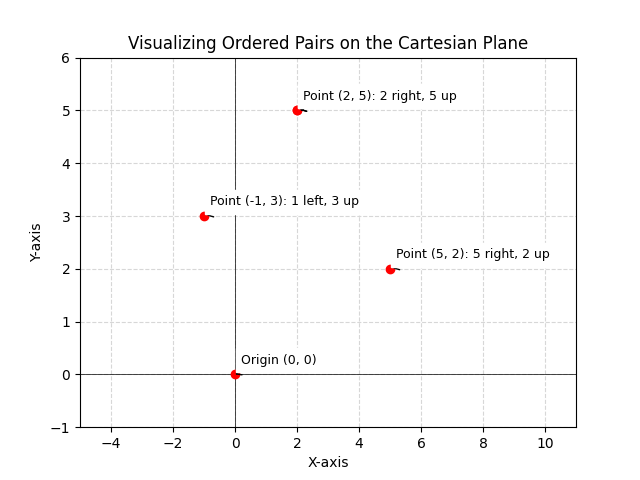
Learn the definition of an ordered pair in mathematics including its key characteristics and applications. Explore examples and understand how it’s used.

The additive inverse of an element, a fundamental concept in mathematics. Learn how to determine it and why it matters.