The Pythagorean Theorem is a cornerstone of geometry, and it’s something we’ll be exploring in detail today. We’ll journey back in time to uncover its origins, and then we’ll break down the theorem itself. We’ll also look at how it’s been proven over the centuries.

Then, we’ll move on to see how the Pythagorean Theorem is actually used in the real world. From construction to navigation, this theorem pops up in some surprising places. Furthermore, we’ll tackle some problems to help you grasp the concepts. So, whether you’re brushing up on your math skills or encountering this for the first time, you’re in the right place.

---

---

This blog post delves into the fascinating world of the Pythagorean Theorem, a cornerstone of geometry. We’ll explore its rich history, understand its formal statement, examine different proofs, and uncover its diverse applications. Whether you’re a student, a teacher, or simply curious about mathematics, this guide will provide a comprehensive understanding of this fundamental theorem. We will also solve several problems to solidify your understanding of the Pythagorean Theorem.

History of the Pythagorean Theorem

The Pythagorean Theorem is one of the oldest and most fundamental concepts in mathematics, with a history that stretches back thousands of years. While often attributed to the Greek mathematician Pythagoras, who lived in the 6th century BC, evidence suggests that the theorem was known and used by earlier civilizations. Babylonian mathematicians, for example, were aware of the relationship between the sides of a right triangle as early as 1900-1600 BC, as evidenced by the Plimpton 322 clay tablet, which contains a table of Pythagorean triples. This tablet demonstrates a sophisticated understanding of right triangles and their properties.

The Egyptians also possessed knowledge related to the theorem, although it is not clear if they had a formal proof. They used ropes with knots spaced at equal intervals to construct right angles, which were essential for surveying and building. Pythagoras and his followers, the Pythagoreans, are credited with providing the first formal proof of the theorem and popularizing its use in mathematics. Their contributions laid the groundwork for much of the geometry we know today, and the theorem’s influence extends far beyond its initial applications in surveying and construction. The theorem’s enduring legacy lies in its simplicity and its profound implications across various fields.

Statement of the Pythagorean Theorem

The Pythagorean Theorem is a fundamental concept in Euclidean geometry that describes the relationship between the sides of a right-angled triangle. A right-angled triangle is a triangle where one of the angles is 90 degrees. The side opposite the right angle is called the hypotenuse, and it is the longest side of the triangle. The other two sides are called legs or cathetus. The theorem states a precise relationship between the lengths of these sides.

Formally,

The Pythagorean Theorem states that in a right-angled triangle, the square of the length of the hypotenuse (c) is equal to the sum of the squares of the lengths of the other two sides (a and b). This relationship is expressed mathematically as: ##a^2 + b^2 = c^2##.

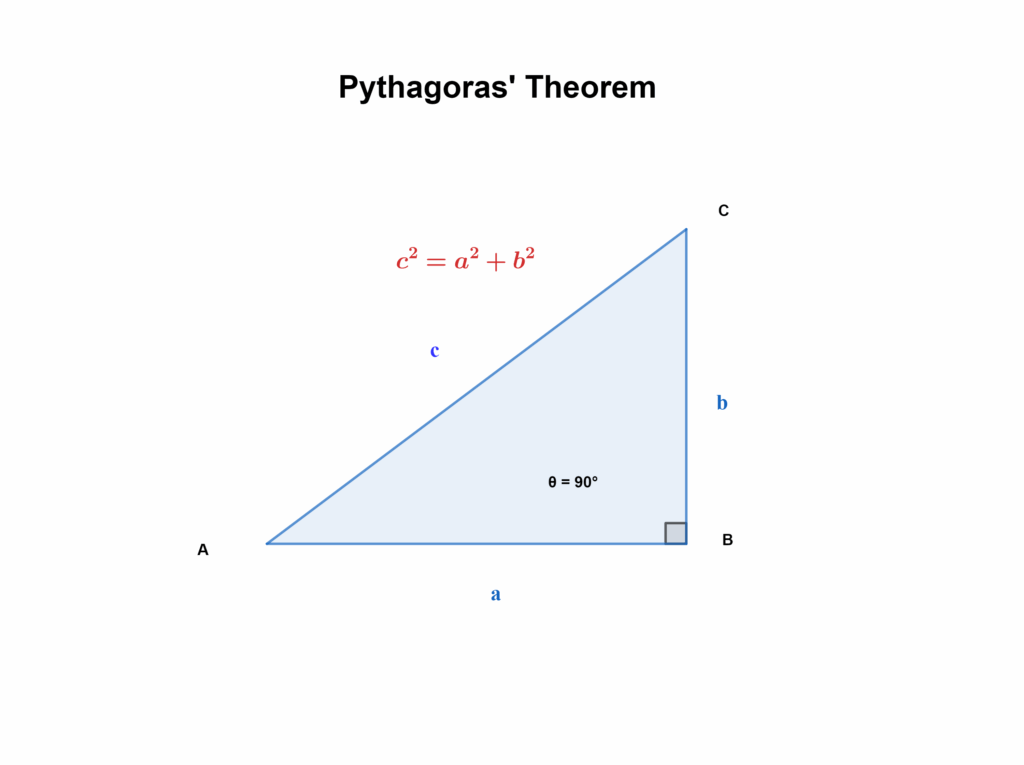
This simple equation has far-reaching implications, allowing us to calculate the length of any side of a right triangle if we know the lengths of the other two sides. It’s a cornerstone of trigonometry and is essential for solving many geometric problems. The theorem’s elegance lies in its simplicity and its wide applicability in various fields.

Pythagorean Theorem Explained: Mathematical Illustration

Let’s visualize the theorem. Imagine a right triangle with legs of length 3 and 4 units, respectively. The hypotenuse, according to the theorem, should have a length of 5 units. This is because ##3^2 + 4^2 = 9 + 16 = 25##, and the square root of 25 is 5. This relationship can be visually represented by constructing squares on each side of the triangle. The area of the square on the hypotenuse is equal to the sum of the areas of the squares on the other two sides. This visual representation helps to understand the theorem’s geometric significance.

For example, if a = 3, b = 4, and c = 5,

then: ### a^2 = 3^2 = 9 ###

### b^2 = 4^2 = 16 ###

### c^2 = 5^2 = 25 ###

Therefore, ##9 + 16 = 25##, which confirms the theorem.

Proofs of the Pythagorean Theorem

There are numerous proofs of the Pythagorean Theorem, demonstrating its fundamental nature and importance in mathematics. One of the most well-known proofs is based on geometric manipulation. It involves making four copies of the triangle and re-arranging them so as to enclose a square. Then by shifting the opposite triangles to unite with each other so as to form a parallelogram, we create a region of two squares. The idea is that the area of the square region before and after re-arrangement remains the same, and we use the area of squares to deduce the Pythagorean Theorem a² + b² = c².

I have created a small video to illustrate this. Hope it will be helpful in understanding.

constructing squares on each side of the right triangle and rearranging the resulting shapes to show that the area of the square on the hypotenuse is equal to the sum of the areas of the squares on the other two sides. This proof is often used in introductory geometry courses due to its visual clarity.

Pythagorean Theorem Explained: Proof by Rearrangement

Another elegant proof involves similar triangles. By drawing an altitude from the right angle to the hypotenuse, the original triangle is divided into two smaller triangles that are similar to the original triangle and to each other. Using the properties of similar triangles, we can establish the relationship ##a^2 + b^2 = c^2##. This proof highlights the interconnectedness of geometric concepts and provides a deeper understanding of the theorem’s underlying principles. There are also algebraic proofs, which use the properties of areas and algebraic manipulations to arrive at the same conclusion. The variety of proofs underscores the theorem’s significance and its central role in geometry.

Let’s consider a right triangle ABC, where angle B is 90 degrees.

Draw a square on each side of the triangle.

The area of the square on the hypotenuse (AC) is equal to the sum of the areas of the squares on the other two sides (AB and BC).

This can be visualized by rearranging the shapes formed by the squares.

Practical Applications of the Pythagorean Theorem

The Pythagorean Theorem has a wide range of practical applications in various fields. In construction and architecture, it is used to ensure that structures are square and to calculate the lengths of diagonal supports. Surveyors use the theorem to measure distances and determine the layout of land. Navigation relies on the theorem to calculate distances and bearings, particularly in situations where direct measurement is not possible. The theorem is also fundamental in computer graphics, where it is used to calculate distances between points and to perform transformations.

Beyond these fields, the theorem is essential in physics and engineering. It is used in the analysis of forces and vectors, the design of electrical circuits, and the calculation of wave phenomena. The theorem’s versatility makes it an indispensable tool for solving real-world problems. From everyday tasks like hanging a picture straight to complex engineering projects, the Pythagorean Theorem plays a crucial role. Its applications are a testament to its enduring relevance and importance in both theoretical and practical contexts. The theorem is a foundational element in fields such as physics, engineering, and computer graphics.

Problems and Solutions

Problem 1:

A right triangle has legs of length 6 cm and 8 cm. What is the length of the hypotenuse?

Solution: ##c = \sqrt{6^2 + 8^2} = \sqrt{36 + 64} = \sqrt{100} = 10## cm.

Problem 2:

The hypotenuse of a right triangle is 13 inches, and one leg is 5 inches. What is the length of the other leg?

Solution: ##a = \sqrt{13^2 – 5^2} = \sqrt{169 – 25} = \sqrt{144} = 12## inches.

Problem 3:

A ladder leans against a wall. The base of the ladder is 4 feet from the wall, and the ladder reaches 10 feet up the wall. How long is the ladder?

Solution: ##c = \sqrt{4^2 + 10^2} = \sqrt{16 + 100} = \sqrt{116} \approx 10.77## feet.

Problem 4:

Find the diagonal of a rectangle with sides 8 meters and 15 meters.

Solution: ##d = \sqrt{8^2 + 15^2} = \sqrt{64 + 225} = \sqrt{289} = 17## meters.

Problem 5:

A ship sails 12 miles east and then 9 miles north. How far is the ship from its starting point?

Solution: ##d = \sqrt{12^2 + 9^2} = \sqrt{144 + 81} = \sqrt{225} = 15## miles.

Problem 6:

Determine the length of the diagonal of a square with side length 7 cm.

Solution: ##d = \sqrt{7^2 + 7^2} = \sqrt{49 + 49} = \sqrt{98} \approx 9.90## cm.

Problem 7:

A baseball diamond is a square with sides of 90 feet. How far is it from home plate to second base?

Solution: ##d = \sqrt{90^2 + 90^2} = \sqrt{8100 + 8100} = \sqrt{16200} \approx 127.28## feet.

Problem 8:

A tree casts a shadow of 15 feet. If the distance from the top of the tree to the end of the shadow is 25 feet, how tall is the tree?

Solution: ##h = \sqrt{25^2 – 15^2} = \sqrt{625 – 225} = \sqrt{400} = 20## feet.

Problem 9:

A rectangular garden is 10 feet long and 24 feet wide. What is the length of the path that runs diagonally across the garden?

Solution: ##p = \sqrt{10^2 + 24^2} = \sqrt{100 + 576} = \sqrt{676} = 26## feet.

Problem 10:

Two cars leave the same point. One travels north at 60 mph, and the other travels east at 80 mph. How far apart are they after 1 hour?

Solution: ##d = \sqrt{60^2 + 80^2} = \sqrt{3600 + 6400} = \sqrt{10000} = 100## miles.

This guide has provided a comprehensive overview of the Pythagorean Theorem Explained, from its historical roots to its practical applications. The problems and solutions provided should help you solidify your understanding of this fundamental concept in mathematics. Keep practicing, and you’ll master this essential tool.

---

---