Today, we’re going to tackle a fundamental concept in algebra: Line Intercepts . Think of it as the starting point for understanding how lines behave in the coordinate plane. We’ll explore what intercepts are, why they matter, and how to find them. This is a crucial building block for more advanced topics, so paying close attention now will definitely pay off later.

Furthermore, Line Intercepts is more than just a math problem; it’s a tool that helps us visualize and understand linear equations. We’ll cover both the x-intercept and the y-intercept, showing you how to calculate them from different forms of linear equations. Then, we’ll also see how these intercepts apply to real-world scenarios, from economics to physics. So, let’s get started and unravel the mysteries of linear equations!

---

---

The topic of Line intercepts is fundamental in algebra and coordinate geometry, providing a crucial foundation for more advanced mathematical concepts. Whether you’re a student, a teacher, or simply someone curious about mathematics, this guide will help you grasp the essentials of intercepts, their significance, and how to calculate them. We will explore the x-intercept and y-intercept, their graphical representations, and how to find them using various forms of linear equations. Let’s dive in and unravel the secrets of Intercepts of a Line!

Understanding Intercepts of a Line

In the realm of coordinate geometry, the intercepts of a line are the points where the line intersects the coordinate axes. These points are fundamental in understanding the behavior and characteristics of linear equations. There are two primary types of intercepts: the x-intercept and the y-intercept. The x-intercept is the point where the line crosses the x-axis, and the y-intercept is the point where the line crosses the y-axis. Understanding these intercepts is crucial for graphing linear equations and interpreting their meaning in real-world applications. The concept of intercepts helps us visualize the line’s position on the coordinate plane and provides valuable information about its slope and direction. The Intercepts of a Line play a vital role in understanding the behavior of linear functions.

The x-intercept is the point on the line where the y-coordinate is zero. This means that the line crosses the x-axis at this point, and the point is represented as (x, 0). Conversely, the y-intercept is the point on the line where the x-coordinate is zero. This means the line crosses the y-axis at this point, and the point is represented as (0, y). Identifying these intercepts is a key step in graphing linear equations and understanding their properties. For instance, the x-intercept tells us where the function’s value is zero, which is often relevant in solving real-world problems. Similarly, the y-intercept gives us the initial value or starting point of the function. The ability to find and interpret these intercepts is a fundamental skill in algebra and beyond.

Visualizing intercepts is straightforward when considering a graph. The x-intercept is the point where the line “touches” the x-axis, and the y-intercept is where it “touches” the y-axis. The position of these intercepts can vary depending on the equation of the line. For example, a line with a positive slope will typically have both an x-intercept and a y-intercept, unless it passes through the origin (0,0). Lines parallel to the x-axis will have a y-intercept but no x-intercept (unless the line is the x-axis itself), and lines parallel to the y-axis will have an x-intercept but no y-intercept (unless the line is the y-axis itself). Understanding these graphical representations is crucial for interpreting the behavior of linear equations and their real-world applications. The Intercepts of a Line provide a visual key to understanding linear equations.

Finding Intercepts: Step-by-Step Guide

Finding the intercepts of a line is a fundamental skill in algebra. The process involves substituting specific values into the equation of the line and solving for the remaining variable. The key is to remember that the x-intercept occurs when y = 0, and the y-intercept occurs when x = 0. Let’s break down the steps for finding both intercepts. This method works regardless of the form in which the linear equation is presented. The ability to find these intercepts is essential for graphing lines and understanding their properties. Let’s explore the process with examples, making it easy to grasp and apply. The correct identification of Intercepts of a Line is crucial for accurate graphing and problem-solving.

Finding the X-intercept

To find the x-intercept, you need to determine the point where the line crosses the x-axis. This occurs when the y-coordinate is zero. The steps are as follows: First, start with the equation of the line. Second, substitute y = 0 into the equation. Third, solve the resulting equation for x. The value of x you find is the x-coordinate of the x-intercept. The x-intercept is then written as a coordinate pair (x, 0). This process is straightforward and can be applied to any linear equation. Let’s look at an example to clarify the process and solidify your understanding. Remember, the x-intercept is where the line meets the x-axis. The Intercepts of a Line are easily found using these steps.

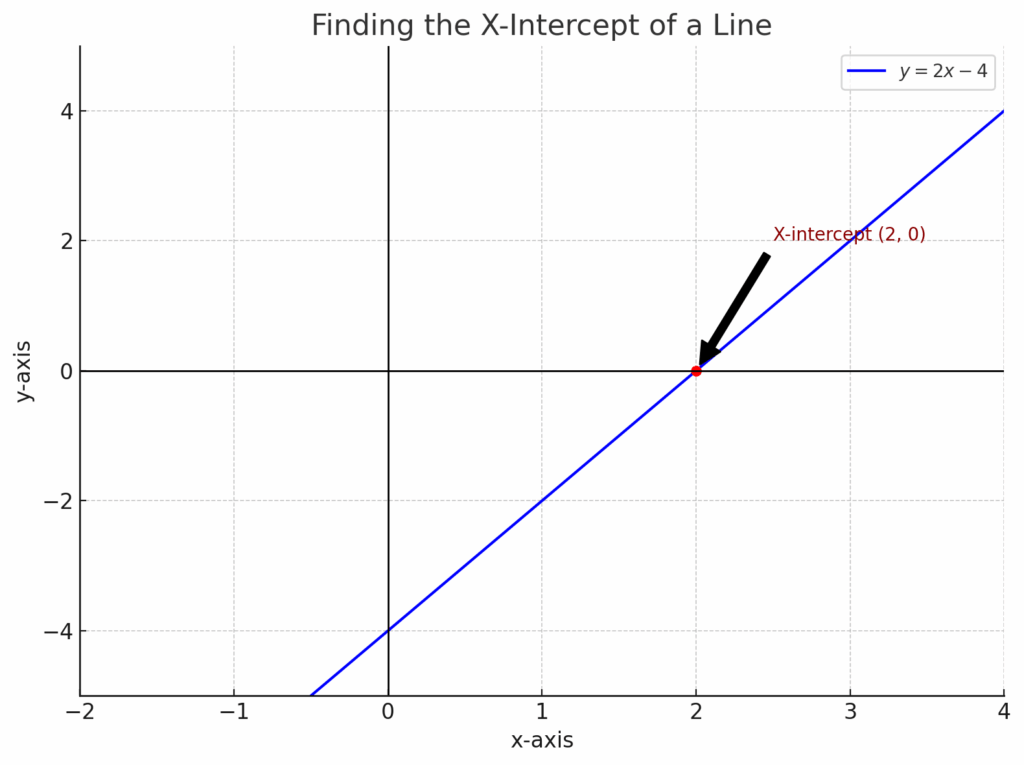
It shows:

• The line y=2x−4
• The x-intercept clearly marked at (2,0) with a red point,

Finding the Y-intercept

To find the y-intercept, you need to determine the point where the line crosses the y-axis. This occurs when the x-coordinate is zero. The steps are as follows: First, start with the equation of the line. Second, substitute x = 0 into the equation. Third, solve the resulting equation for y. The value of y you find is the y-coordinate of the y-intercept. The y-intercept is then written as a coordinate pair (0, y). This process is equally straightforward and can be applied to any linear equation. Let’s look at an example to clarify the process and solidify your understanding. Remember, the y-intercept is where the line meets the y-axis. Correctly identifying the Intercepts of a Line is essential for understanding the equation.

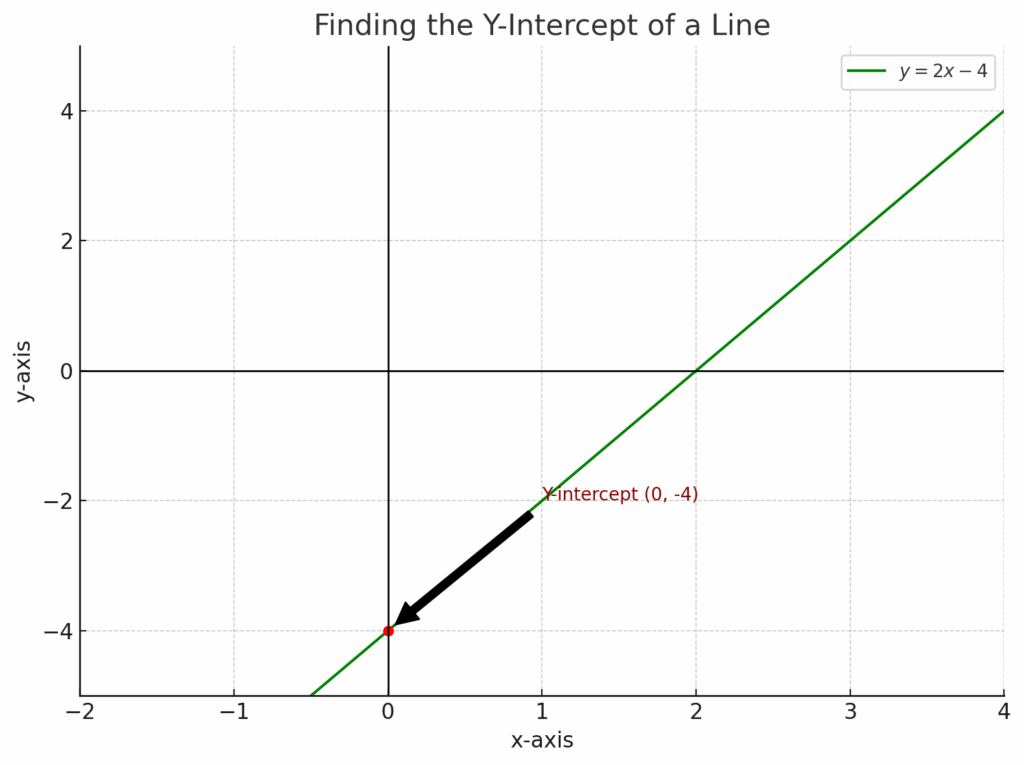
Here’s the diagram for Finding the Y-Intercept!

It clearly shows:

• The line y=2x−4
• The y-intercept marked at (0,−4 with a red point,

Illustrative Example

Let’s consider the linear equation: ##2x + 3y = 6##. To find the x-intercept, we substitute ##y = 0##: ##2x + 3(0) = 6##, which simplifies to ##2x = 6##. Solving for x, we get ##x = 3##. Therefore, the x-intercept is (3, 0). To find the y-intercept, we substitute ##x = 0##: ##2(0) + 3y = 6##, which simplifies to ##3y = 6##. Solving for y, we get ##y = 2##. Therefore, the y-intercept is (0, 2). This example clearly demonstrates how to find both intercepts. By following these steps, you can easily determine the intercepts of any linear equation. The Intercepts of a Line provide key points for graphing the line.

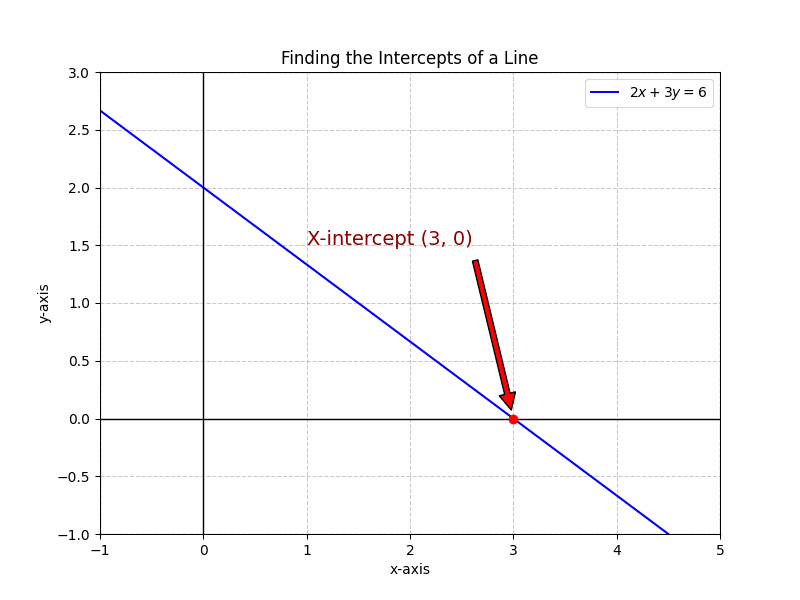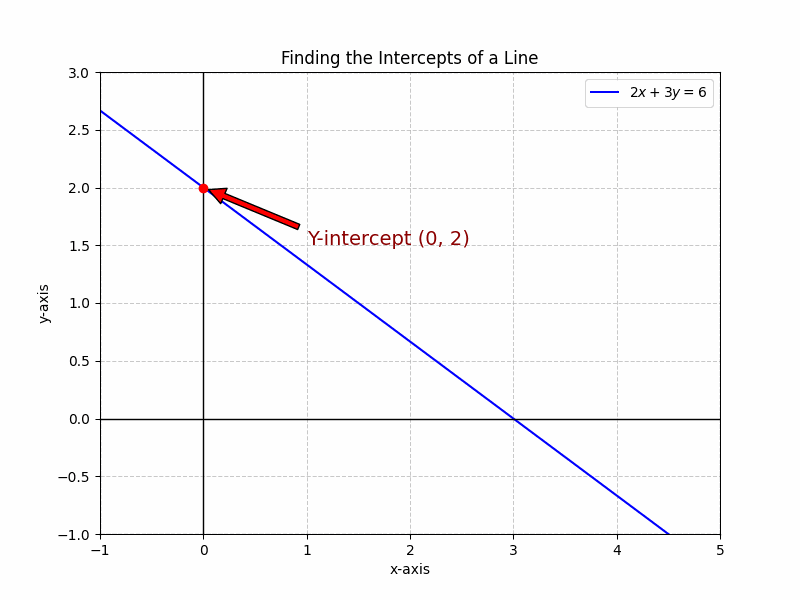
Different Forms of Linear Equations and Their Intercepts

Linear equations can be expressed in various forms, each with its unique characteristics. The most common forms are the slope-intercept form, the standard form, and the point-slope form. Understanding how to find intercepts in each of these forms is crucial for efficiently solving problems and interpreting the equations. Each form offers a different perspective on the line’s properties, and knowing how to work with each one enhances your problem-solving skills. The Intercepts of a Line are easily determined once the equation is in a suitable form. Let’s delve into each form and see how to find the intercepts.

Slope-Intercept Form

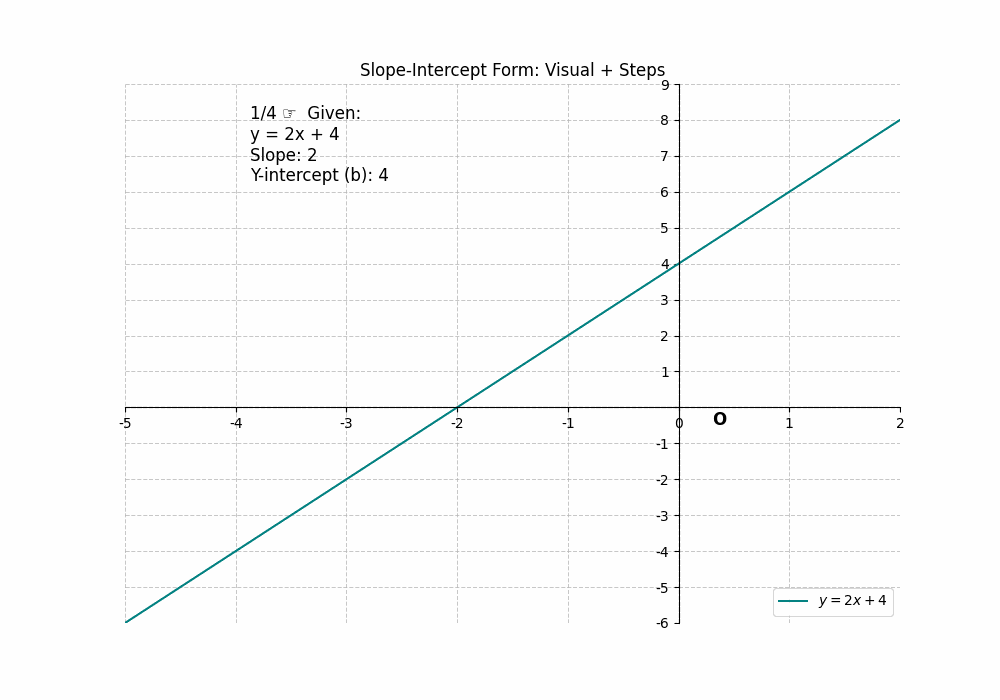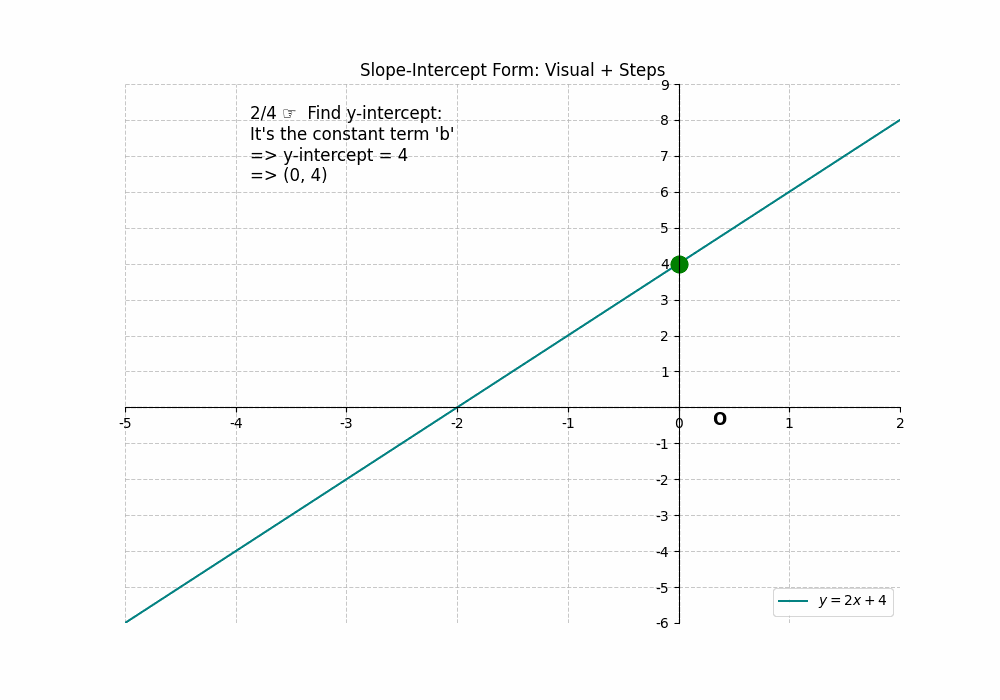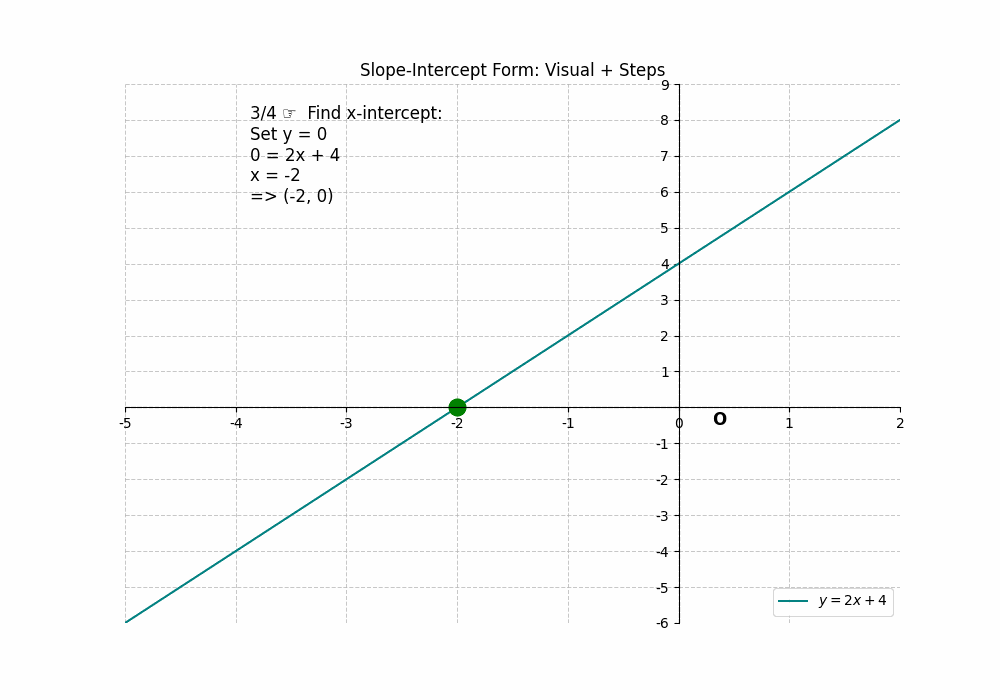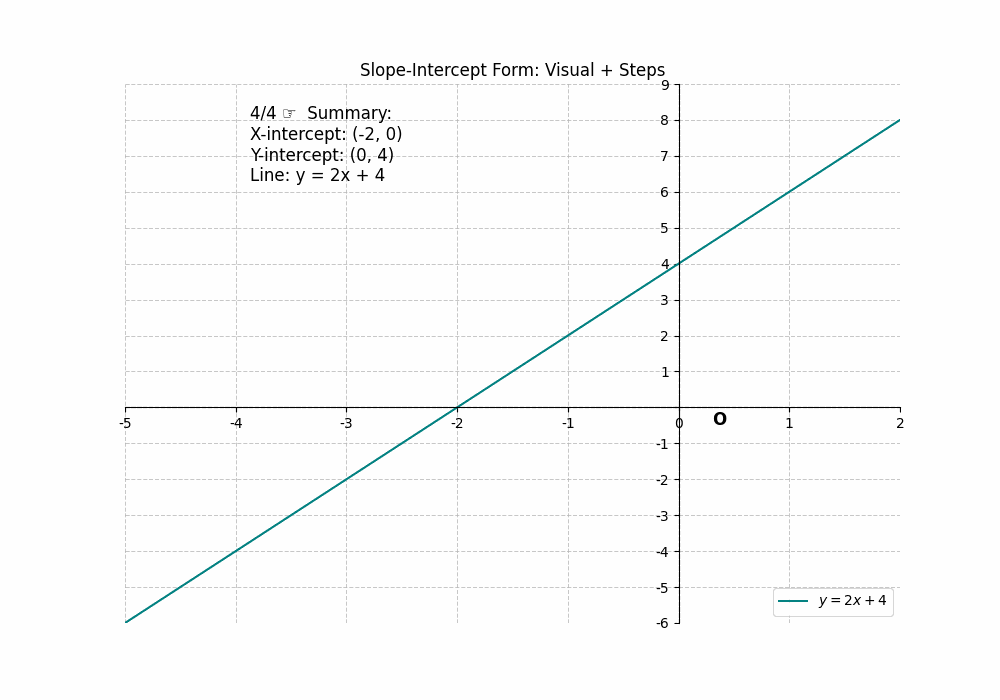
The slope-intercept form of a linear equation is ##y = mx + b##, where ‘m’ represents the slope and ‘b’ represents the y-intercept. Finding the y-intercept is straightforward: it’s the value of ‘b’. To find the x-intercept, set ##y = 0## and solve for x: ##0 = mx + b##, which gives ##x = -\frac{b}{m}##. For example, in the equation ##y = 2x + 4##, the y-intercept is 4 (0, 4), and the x-intercept is ##-\frac{4}{2} = -2## (-2, 0). This form makes it easy to identify the y-intercept directly and quickly calculate the x-intercept. The Intercepts of a Line are readily available in the slope-intercept form.

Standard Form

The standard form of a linear equation is ##Ax + By = C##. To find the x-intercept, set ##y = 0## and solve for x: ##Ax + B(0) = C##, which gives ##x = \frac{C}{A}##. To find the y-intercept, set ##x = 0## and solve for y: ##A(0) + By = C##, which gives ##y = \frac{C}{B}##. For example, in the equation ##3x + 4y = 12##, the x-intercept is ##\frac{12}{3} = 4## (4, 0), and the y-intercept is ##\frac{12}{4} = 3## (0, 3). This form requires a bit more calculation, but the process is still straightforward. The Intercepts of a Line can be easily determined using the standard form.

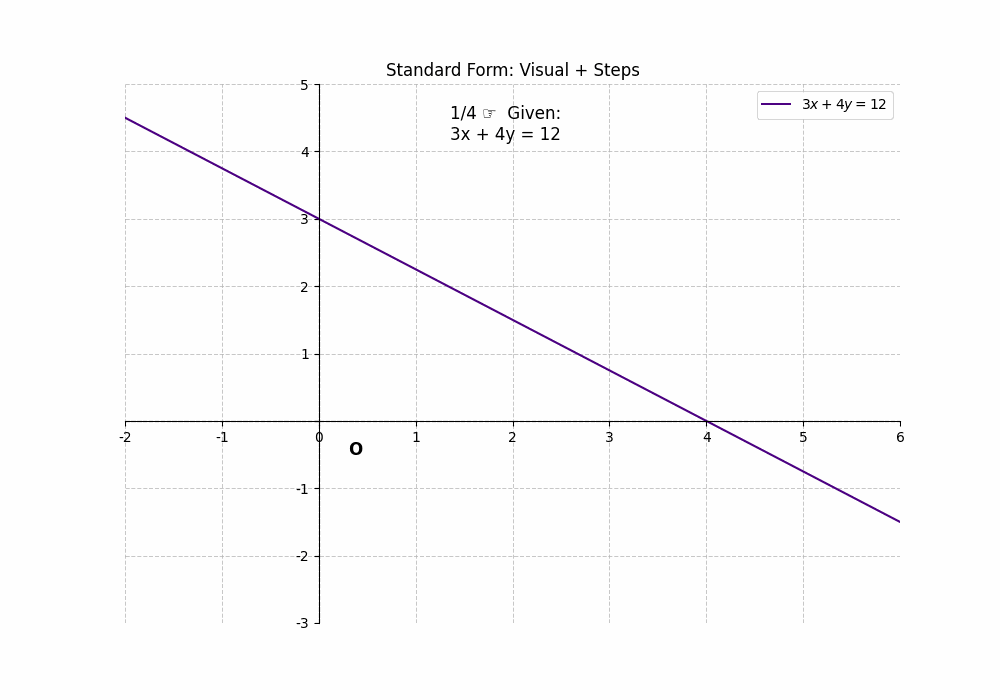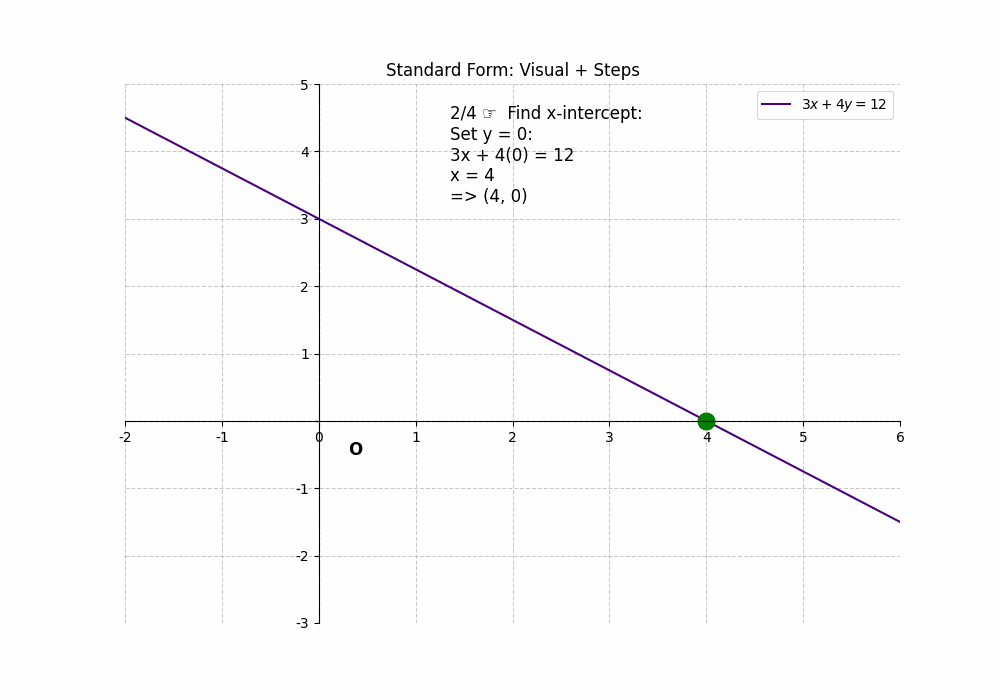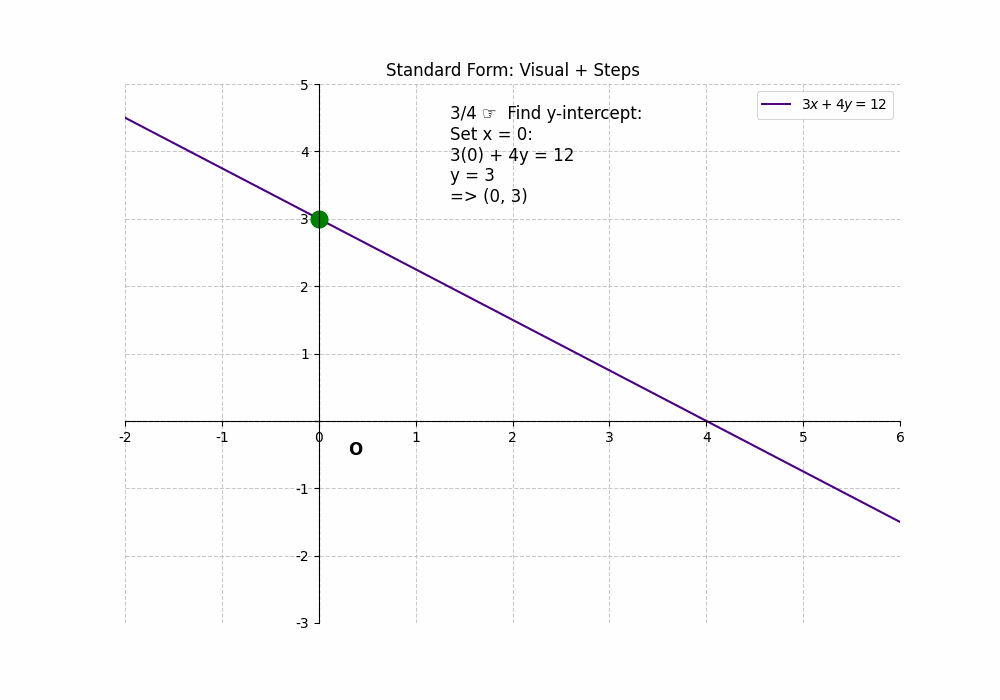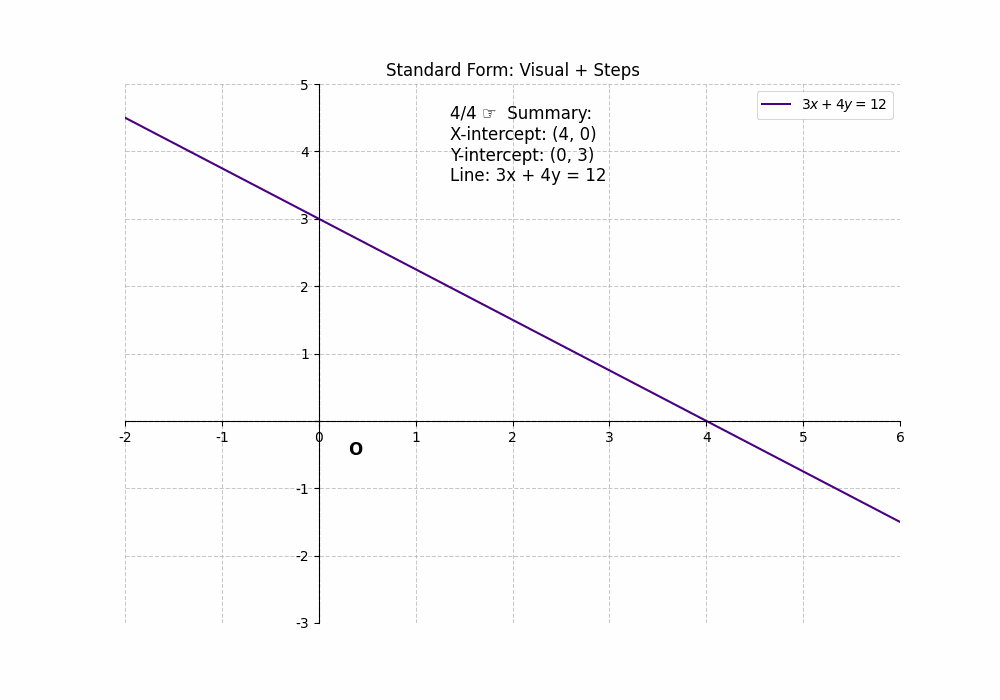
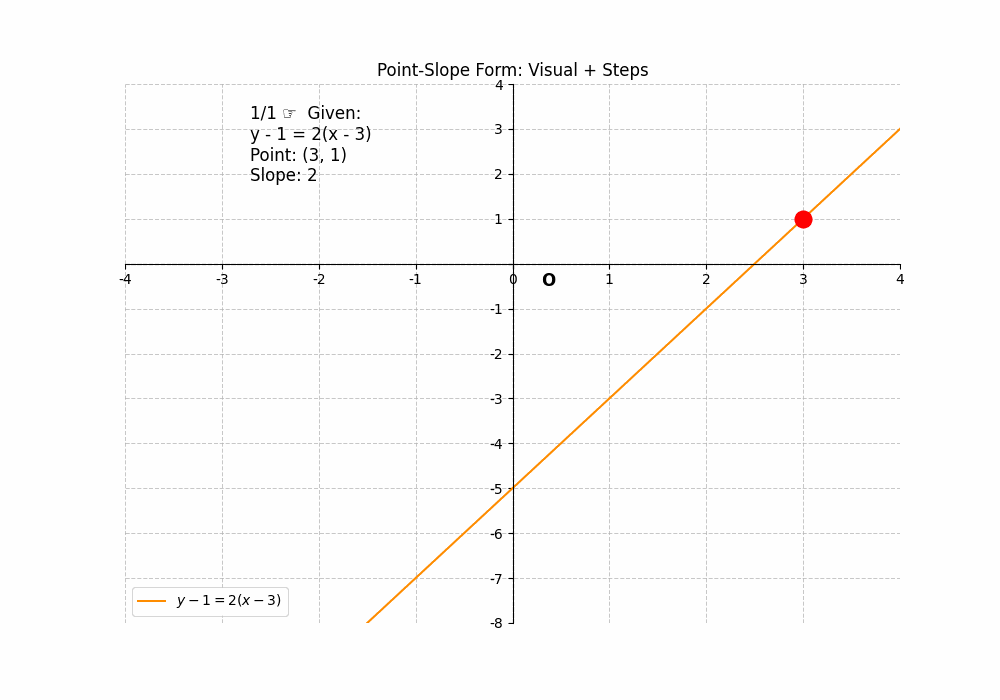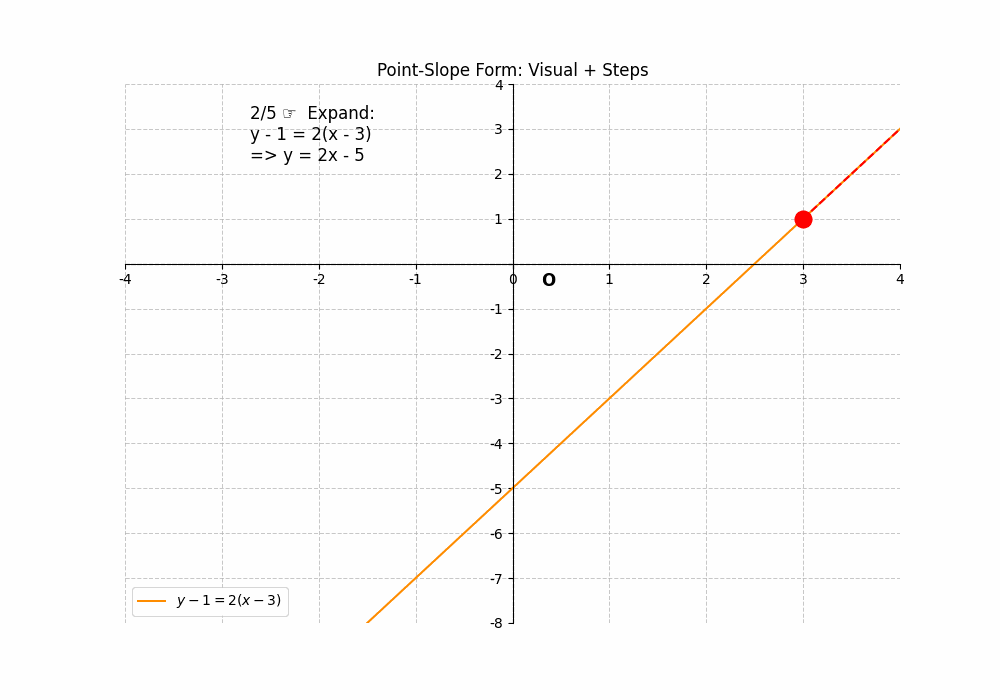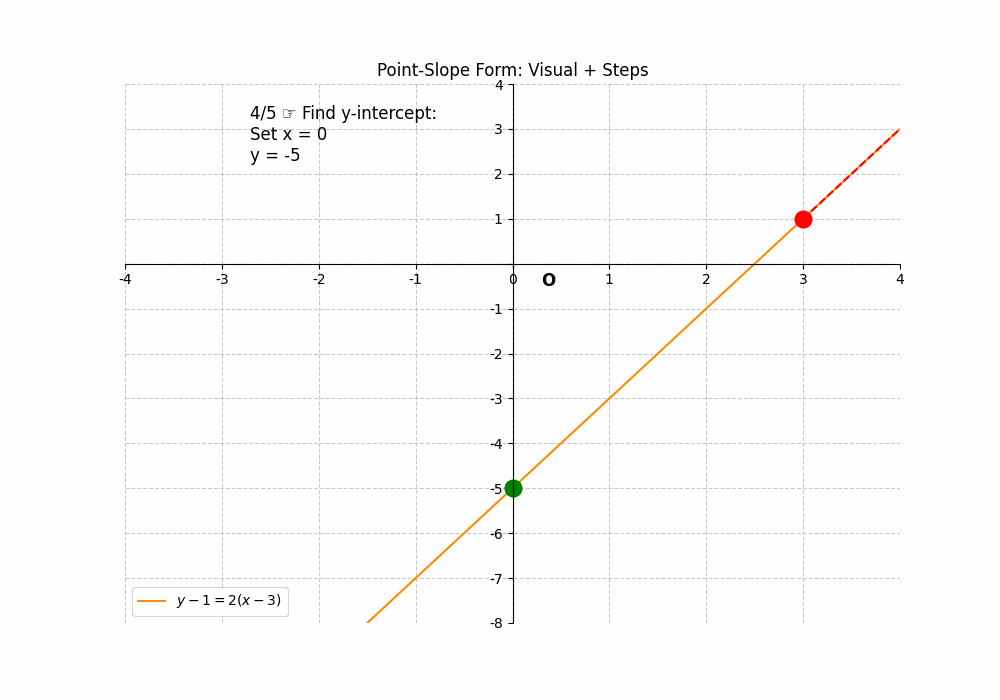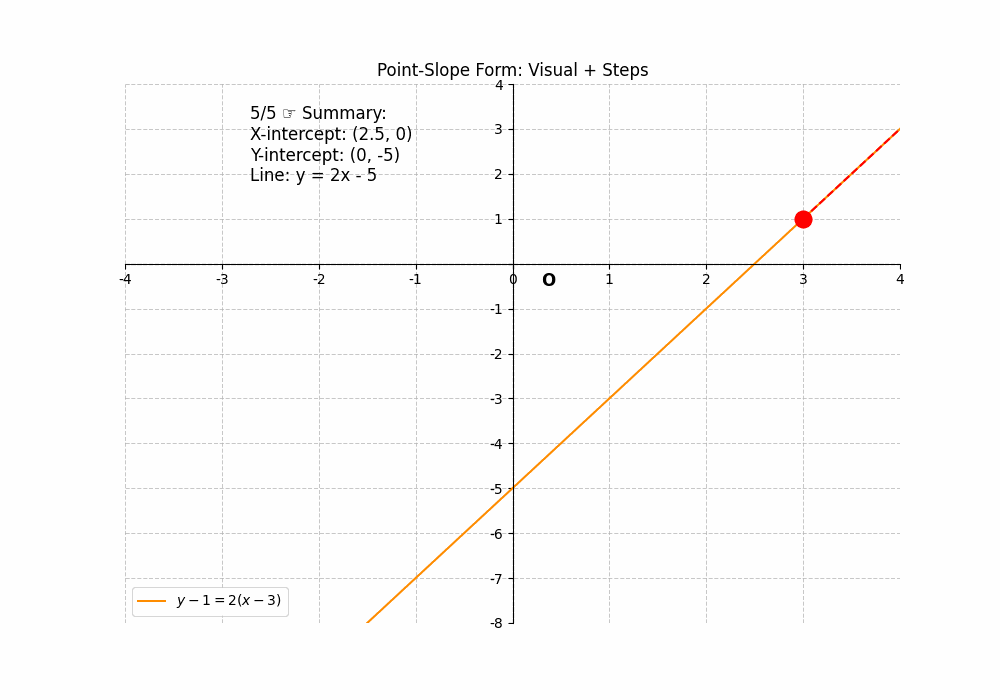
Point-Slope Form

The point-slope form of a linear equation is ##y – y_1 = m(x – x_1)##, where (x1, y1) is a point on the line and ‘m’ is the slope. To find the x-intercept, set ##y = 0## and solve for x: ##0 – y_1 = m(x – x_1)##, which gives ##x = x_1 – \frac{y_1}{m}##. To find the y-intercept, set ##x = 0## and solve for y: ##y – y_1 = m(0 – x_1)##, which gives ##y = y_1 – mx_1##. For example, if the equation is ##y – 1 = 2(x – 3)##, the x-intercept is ##3 – \frac{1}{2} = 2.5## (2.5, 0), and the y-intercept is ##1 – 2(3) = -5## (0, -5). While this form requires more algebraic manipulation, the intercepts can still be found. The Intercepts of a Line can be found using the point-slope form.

Graphical Representation of Intercepts

Graphing intercepts is a fundamental skill in understanding linear equations. The x-intercept and y-intercept provide two crucial points that define the line’s position on the coordinate plane. By plotting these points and connecting them with a straight line, you can visually represent the equation. This graphical representation helps in understanding the line’s slope, direction, and its relationship with the coordinate axes. The ability to graph intercepts is a key step in visualizing and interpreting linear equations. Let’s explore how to graph intercepts and understand their graphical significance. The Intercepts of a Line are essential for graphical representation.

Plotting the Intercepts

To graph a line using its intercepts, first, find the x-intercept and the y-intercept. The x-intercept is a point on the x-axis, so its y-coordinate is always 0, and the y-intercept is a point on the y-axis, so its x-coordinate is always 0. Plot these two points on the coordinate plane. Once you have plotted the x-intercept and the y-intercept, draw a straight line that passes through both points. This line represents the graph of the linear equation. This simple process provides a clear visual representation of the equation. The Intercepts of a Line are easily plotted on a graph.

Interpreting the Graph

The graph of a line provides valuable information about the linear equation. The slope of the line can be determined by observing its direction. A line that slopes upwards from left to right has a positive slope, while a line that slopes downwards from left to right has a negative slope. The y-intercept indicates the point where the line crosses the y-axis, which is the initial value or starting point of the function. The x-intercept indicates where the function’s value is zero, which can be crucial in solving real-world problems. By analyzing the graph, you can understand the relationship between the variables and interpret the equation’s meaning. The Intercepts of a Line help in interpreting the graph.

Example of Graphing

Consider the equation ##2x + 3y = 6##. We found earlier that the x-intercept is (3, 0) and the y-intercept is (0, 2). To graph this equation, plot the points (3, 0) and (0, 2) on the coordinate plane. Then, draw a straight line that passes through both points. This line represents the graph of the equation ##2x + 3y = 6##. The slope of the line is negative, and it crosses the y-axis at the point (0, 2). This example illustrates how easy it is to graph a line using its intercepts. The Intercepts of a Line make graphing linear equations simple.

Applications of Intercepts in Real-World Problems

Intercepts are not just abstract mathematical concepts; they have practical applications in various real-world scenarios. They help in modeling and understanding linear relationships in fields such as economics, physics, and everyday life situations. Understanding intercepts allows us to interpret data, make predictions, and solve problems effectively. The x-intercept and y-intercept provide valuable insights into the behavior of linear models. Let’s explore some examples of how intercepts are used in real-world problems. The Intercepts of a Line are essential for real-world applications.

Economics and Finance

In economics and finance, intercepts are used to analyze cost, revenue, and profit functions. The y-intercept often represents the fixed costs, such as rent or salaries, which are incurred even when no goods or services are produced. The x-intercept can represent the break-even point, where the revenue equals the total cost. For example, in a cost function ##C(x) = 100 + 5x##, where x is the number of items produced, the y-intercept is 100, representing the fixed costs. The x-intercept would be where the cost is zero, which is not typically relevant in this context, but it helps to understand the function’s behavior. The Intercepts of a Line are useful in economic analysis.

Physics and Engineering

In physics and engineering, intercepts are used to model linear relationships, such as the motion of an object or the relationship between voltage and current. The y-intercept might represent the initial position or velocity of an object. The x-intercept could represent the time when the object reaches a certain position or the point where a circuit is open. For example, in the equation of motion ##d = vt + d_0##, where d is the distance, v is the velocity, t is the time, and d0 is the initial distance, the y-intercept is d0. The x-intercept would be the time when the distance is zero. The Intercepts of a Line are valuable in physics and engineering.

Everyday Life Examples

Intercepts can also be found in everyday life. For example, consider the cost of a taxi ride, which often has a fixed charge (y-intercept) and a per-mile charge (slope). The y-intercept is the initial fee, and the slope represents the cost per mile. The x-intercept would be the point where the total cost is zero, which is not usually relevant in this context. Another example is the relationship between the amount of water in a tank and the time it takes to drain. The y-intercept is the initial amount of water, and the x-intercept is the time when the tank is empty. The Intercepts of a Line help in understanding everyday scenarios.

Common Mistakes and How to Avoid Them

While finding intercepts seems straightforward, there are common mistakes that students often make. Recognizing these mistakes and understanding how to avoid them can significantly improve your accuracy and understanding. Let’s explore some common pitfalls and how to overcome them. By being aware of these common errors, you can approach problems with greater confidence and precision. The Intercepts of a Line require careful attention to detail to avoid mistakes.

Incorrect Substitution

One common mistake is incorrectly substituting the values of x and y. Remember that to find the x-intercept, you must set y = 0, and to find the y-intercept, you must set x = 0. Double-check your substitutions to ensure they are correct. For example, if you are given the equation ##2x + 3y = 6##, and you want to find the x-intercept, you should substitute ##y = 0##, not ##x = 0##. Always write down the substitution explicitly to avoid confusion. This simple step can prevent many errors. The Intercepts of a Line are easily found with correct substitution.

Misinterpreting the Results

Another common mistake is misinterpreting the results. Remember that the x-intercept is a point on the x-axis, and the y-intercept is a point on the y-axis. Therefore, the x-intercept is written as (x, 0), and the y-intercept is written as (0, y). Make sure you correctly identify the coordinates of the intercepts. For example, if you find that x = 3, the x-intercept is (3, 0), not just 3. Always write the intercepts as ordered pairs. This will help you avoid confusion when graphing the line. The Intercepts of a Line should be correctly interpreted.

Incorrect Algebraic Manipulation

Incorrect algebraic manipulation is another source of errors. When solving for x or y, ensure you follow the correct order of operations and use the correct algebraic techniques. Double-check your calculations to avoid making mistakes. For example, when solving for x in the equation ##2x = 6##, you should divide both sides by 2, not multiply. Always review your steps to ensure you have performed the calculations correctly. This will help you arrive at the correct intercepts. The Intercepts of a Line require accurate algebraic manipulation.

Practice Problems and Solutions

Practice is key to mastering any mathematical concept. Here are some practice problems to help you solidify your understanding of intercepts. Try solving these problems on your own, and then check your answers against the provided solutions. This practice will help you build confidence and improve your problem-solving skills. The Intercepts of a Line are best understood through practice. Let’s get started with some practice problems.

Problem 1

Find the x-intercept and y-intercept of the line: ##y = 3x – 6##.

Solution: x-intercept: (2, 0), y-intercept: (0, -6)

Problem 2

Find the x-intercept and y-intercept of the line: ##2x + 5y = 10##.

Solution: x-intercept: (5, 0), y-intercept: (0, 2)

Problem 3

Find the x-intercept and y-intercept of the line: ##y – 2 = \frac{1}{2}(x + 4)##.

Solution: x-intercept: (-8, 0), y-intercept: (0, 4)

Problem 4

Find the x-intercept and y-intercept of the line: ##y = -x + 3##.

Solution: x-intercept: (3, 0), y-intercept: (0, 3)

Problem 5

Find the x-intercept and y-intercept of the line: ##4x – 2y = 8##.

Solution: x-intercept: (2, 0), y-intercept: (0, -4)

Additional Problems for Further Practice

To further enhance your understanding, here are some additional problems for you to practice. These problems cover various forms of linear equations and different scenarios. Working through these problems will reinforce your skills and prepare you for more complex mathematical concepts. Remember to follow the steps we discussed earlier, and don’t hesitate to review the explanations if you get stuck. The Intercepts of a Line can be mastered with consistent practice. Let’s tackle these additional problems.

Problem 1

Find the x-intercept and y-intercept of the line: ##y = -2x + 8##.

Solution: x-intercept: (4, 0), y-intercept: (0, 8)

Problem 2

Find the x-intercept and y-intercept of the line: ##3x – 4y = 12##.

Solution: x-intercept: (4, 0), y-intercept: (0, -3)

Problem 3

Find the x-intercept and y-intercept of the line: ##y + 1 = \frac{2}{3}(x – 3)##.

Solution: x-intercept: (0, 0), y-intercept: (0, 1)

Problem 4

Find the x-intercept and y-intercept of the line: ##y = x – 5##.

Solution: x-intercept: (5, 0), y-intercept: (0, -5)

Problem 5

Find the x-intercept and y-intercept of the line: ##5x + 2y = 10##.

Solution: x-intercept: (2, 0), y-intercept: (0, 5)