Alright, let’s get started with a clear explanation of the topic. You’re here to learn about the Midpoint Formula , and that’s precisely what we’ll cover. This formula is a fundamental concept in coordinate geometry, and understanding it is key to unlocking a deeper understanding of various geometric principles. We’ll break down the formula, explore its applications, and work through examples to make sure you grasp the concepts thoroughly.

Understanding the Midpoint Formula

The Midpoint Formula is a cornerstone of coordinate geometry, providing a straightforward method to determine the coordinates of the midpoint of a line segment. The midpoint is, by definition, the point that lies exactly halfway between two given points on a coordinate plane. This concept is not only crucial for solving geometric problems but also serves as a building block for more advanced topics in mathematics. Understanding the Midpoint Formula is essential for anyone delving into geometry, as it helps in determining the center of various shapes and solving a wide array of problems.

The formula itself is elegant and easy to remember. Given two points, ##(x_1, y_1)## and ##(x_2, y_2)##, the midpoint ##(x_m, y_m)## is calculated by averaging the x-coordinates and averaging the y-coordinates. This simple averaging process ensures that the midpoint is equidistant from both endpoints of the line segment. This is because the midpoint formula essentially finds the average position in both the x and y directions. This ensures that the midpoint lies exactly in the middle of the line segment, as expected.

The applications of the Midpoint Formula extend beyond simple calculations. It is used in various areas of mathematics, including finding the center of a circle given the endpoints of a diameter, determining the centroid of a triangle, and solving problems related to geometric shapes. The ability to quickly and accurately find the midpoint is a valuable skill in geometry, making it easier to analyze and solve complex problems. Furthermore, the formula provides a visual and intuitive way to understand the concept of averaging and coordinate systems.

How to Use the Midpoint Formula

The Midpoint Formula is expressed as follows: If we have two points, ##(x_1, y_1)## and ##(x_2, y_2)##, the midpoint ##(x_m, y_m)## is given by:

### (x_m, y_m) = \left(\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}\right) ###

This formula is the heart of the concept. It tells us that the x-coordinate of the midpoint is the average of the x-coordinates of the two endpoints, and the y-coordinate of the midpoint is the average of the y-coordinates of the two endpoints. This simple averaging process guarantees that the midpoint lies exactly in the middle of the line segment. It is a fundamental tool in coordinate geometry, used to find the center of various geometric shapes and to solve a variety of problems.

Step-by-Step Guide

Let’s break down the process step-by-step to ensure clarity:

1. Identify the Coordinates: First, identify the coordinates of the two endpoints of the line segment. Label them as ##(x_1, y_1)## and ##(x_2, y_2)##.
2. Apply the Formula: Substitute the x-coordinates into the formula ##\frac{x_1 + x_2}{2}## to find the x-coordinate of the midpoint. Similarly, substitute the y-coordinates into the formula ##\frac{y_1 + y_2}{2}## to find the y-coordinate of the midpoint.
3. Calculate the Midpoint: Perform the arithmetic operations (addition and division) to calculate the x and y coordinates of the midpoint.
4. Write the Result: Express the midpoint as an ordered pair ##(x_m, y_m)##.

Example 1: Simple Calculation

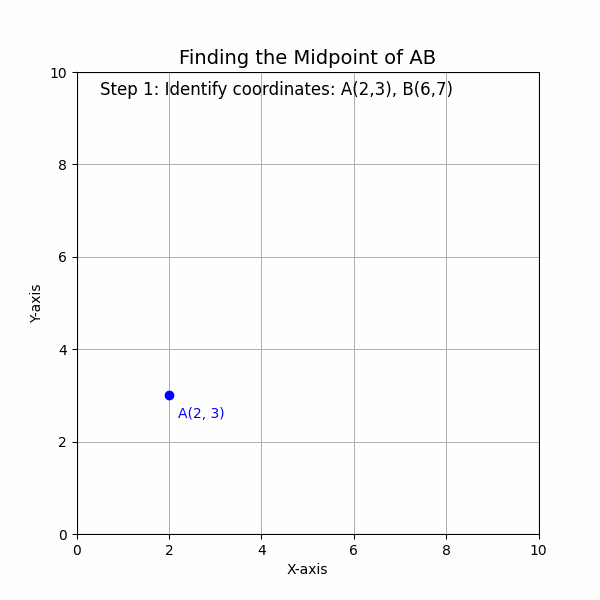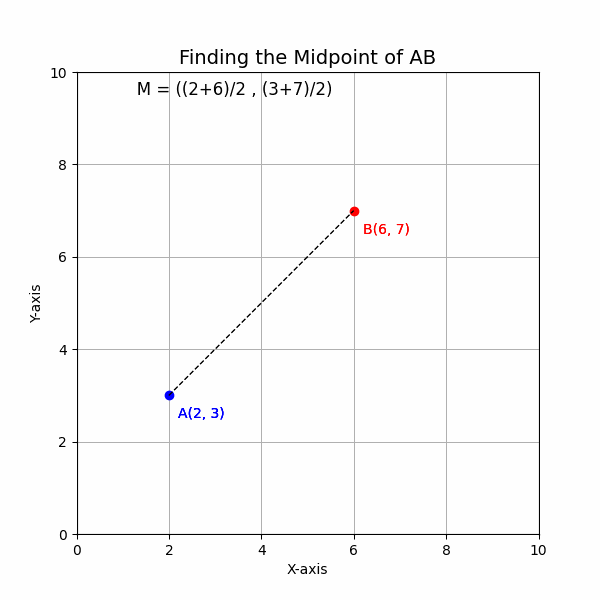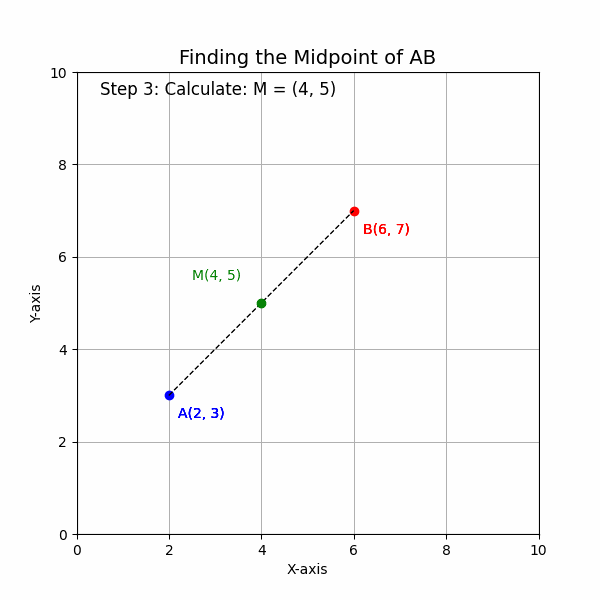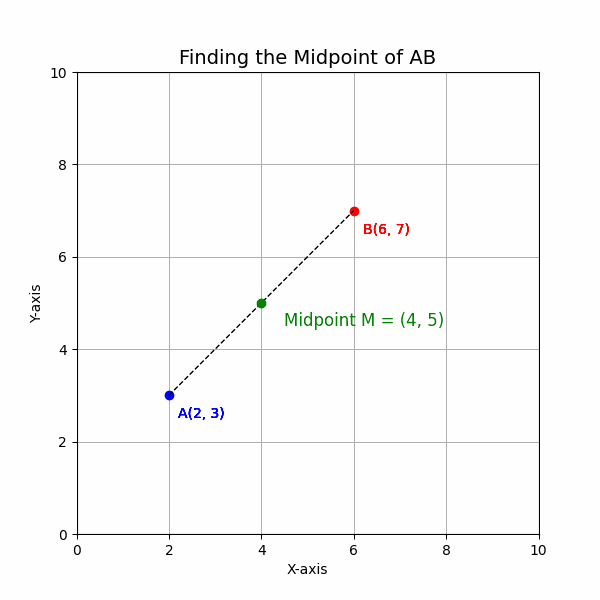
Let’s find the midpoint of the line segment with endpoints A(2, 3) and B(6, 7).

Solution:

1. Identify the coordinates: ##x_1 = 2, y_1 = 3, x_2 = 6, y_2 = 7##

2. Apply the formula:

##x_m = \frac{2 + 6}{2} = \frac{8}{2} = 4##

##y_m = \frac{3 + 7}{2} = \frac{10}{2} = 5##

3. Calculate the Midpoint: The midpoint is (4, 5).

4. Write the Result: The midpoint of the line segment AB is (4, 5).

This example illustrates the straightforward application of the Midpoint Formula. By averaging the x-coordinates and y-coordinates, we easily find the midpoint. This method can be applied to any line segment on a coordinate plane, regardless of the values of the coordinates.

More Examples and Practice

Example 2: Negative Coordinates

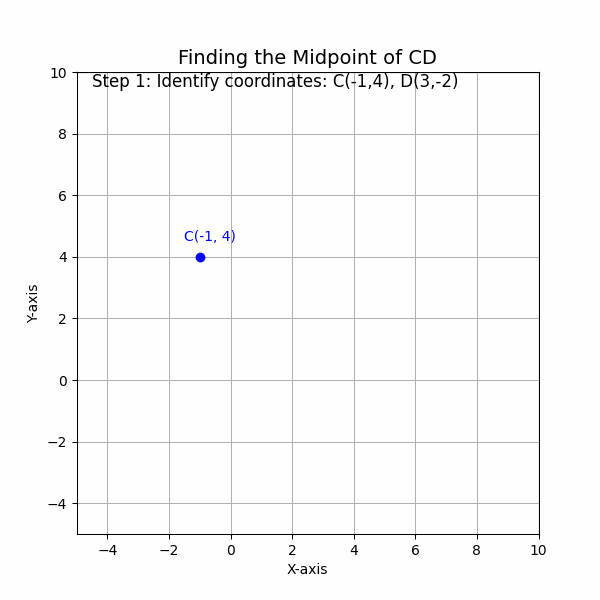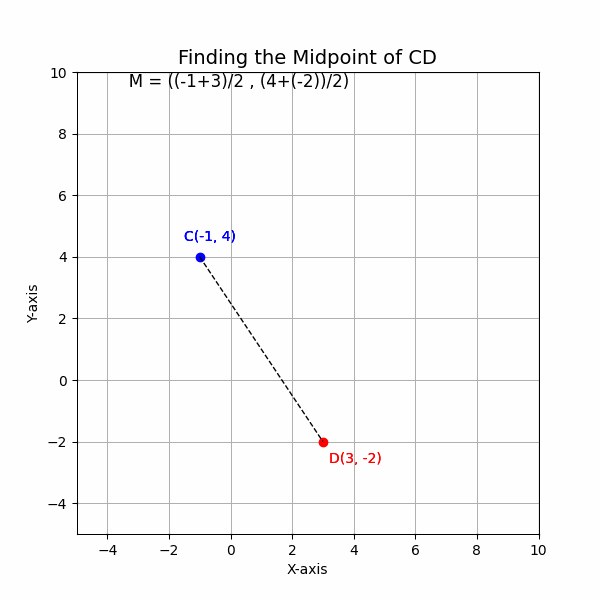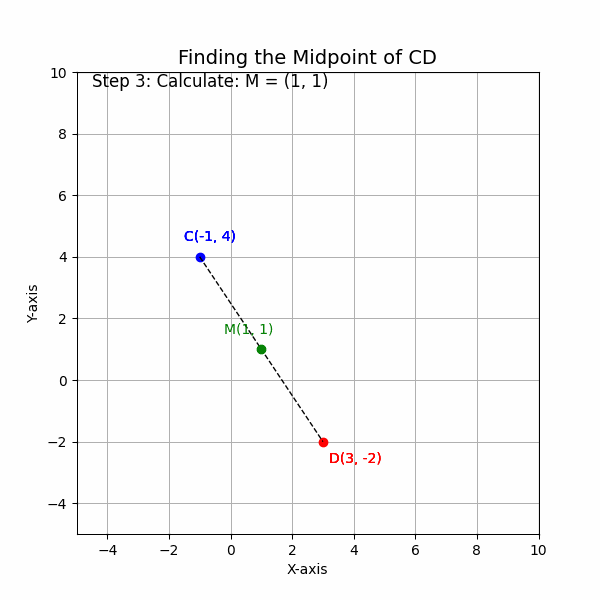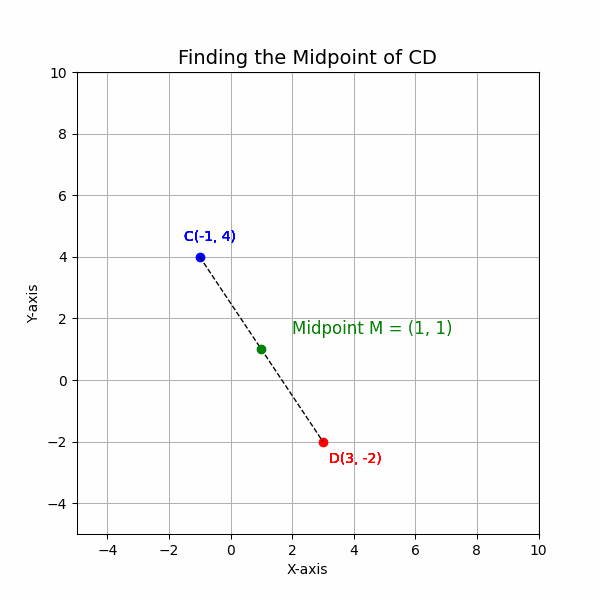
Find the midpoint of the line segment with endpoints C(-1, 4) and D(3, -2).

Solution:

1. Identify the coordinates: ##x_1 = -1, y_1 = 4, x_2 = 3, y_2 = -2##

2. Apply the formula:

##x_m = \frac{-1 + 3}{2} = \frac{2}{2} = 1##

##y_m = \frac{4 + (-2)}{2} = \frac{2}{2} = 1##

3. Calculate the Midpoint: The midpoint is (1, 1).

4. Write the Result: The midpoint of the line segment CD is (1, 1).

This example demonstrates how to handle negative coordinates. The process remains the same; simply ensure that you correctly add and subtract the values. The Midpoint Formula works consistently, regardless of the sign of the coordinates. This reinforces the versatility and reliability of the formula in various scenarios.

Example 3: Fractional Coordinates

Find the midpoint of the line segment with endpoints E(1/2, 5) and F(3/2, 1).

Solution:

1. Identify the coordinates: ##x_1 = 1/2, y_1 = 5, x_2 = 3/2, y_2 = 1##

2. Apply the formula:

##x_m = \frac{1/2 + 3/2}{2} = \frac{4/2}{2} = \frac{2}{2} = 1##

##y_m = \frac{5 + 1}{2} = \frac{6}{2} = 3##

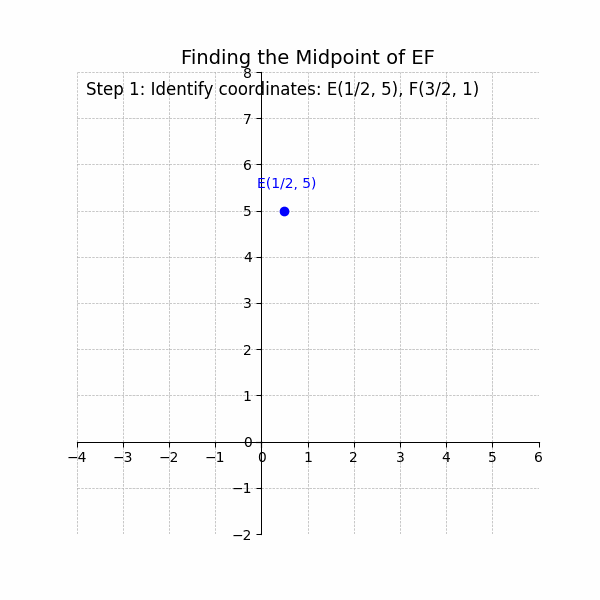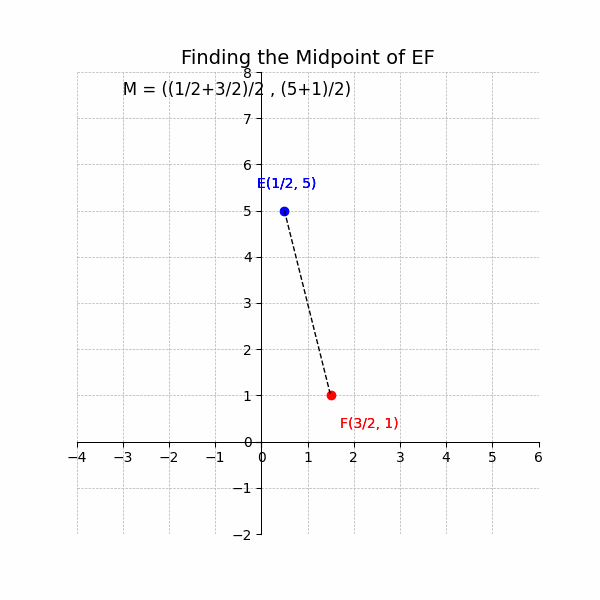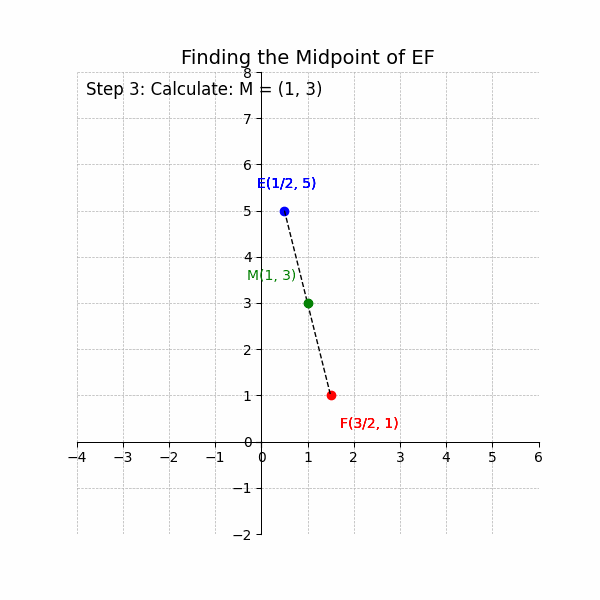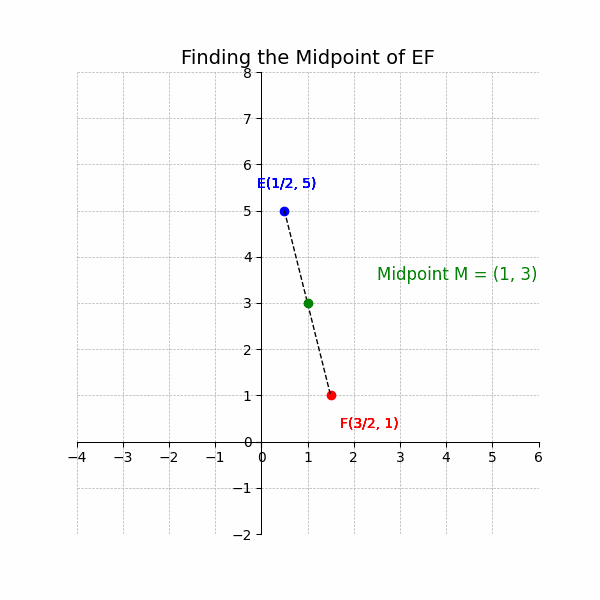
3. Calculate the Midpoint: The midpoint is (1, 3).

4. Write the Result: The midpoint of the line segment EF is (1, 3).

This example shows how to work with fractional coordinates. The Midpoint Formula is equally applicable when dealing with fractions. The key is to correctly perform the addition and division operations. This example highlights the adaptability of the formula to different types of numerical values, ensuring that it can be used in a wide range of mathematical problems.

Applications of the Midpoint Formula

The Midpoint Formula is not just a standalone concept; it’s a versatile tool with various applications in geometry and related fields. Understanding these applications will further solidify your grasp of the formula and its importance.

Finding the Center of a Circle

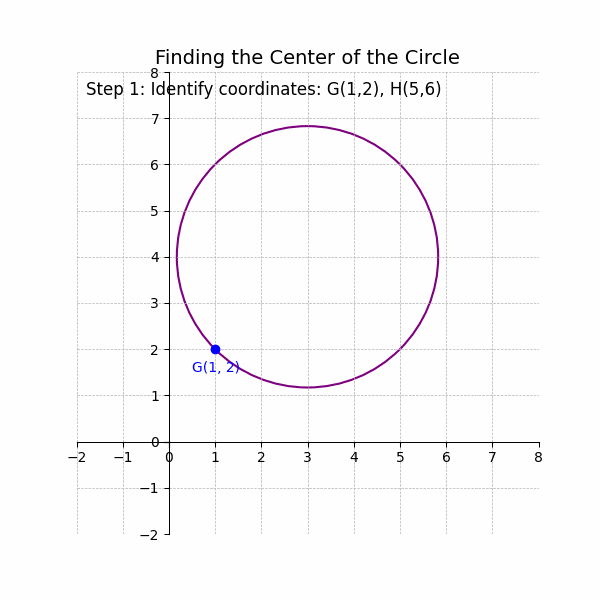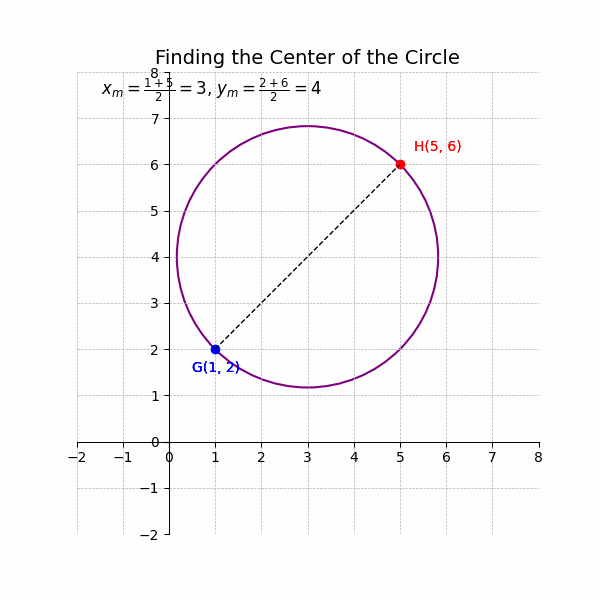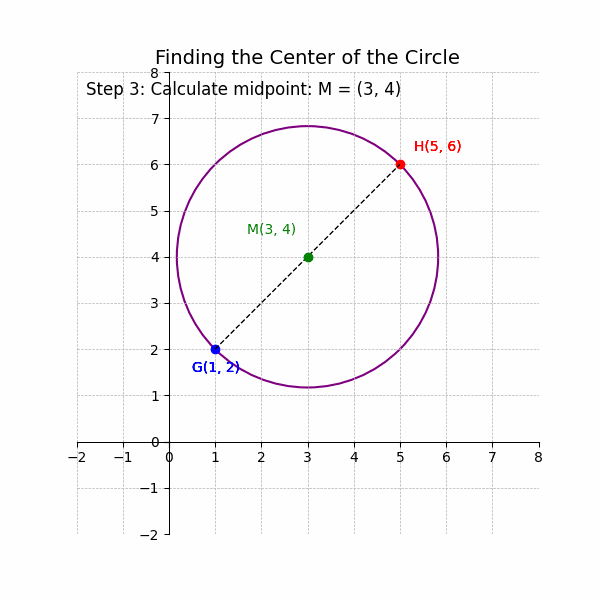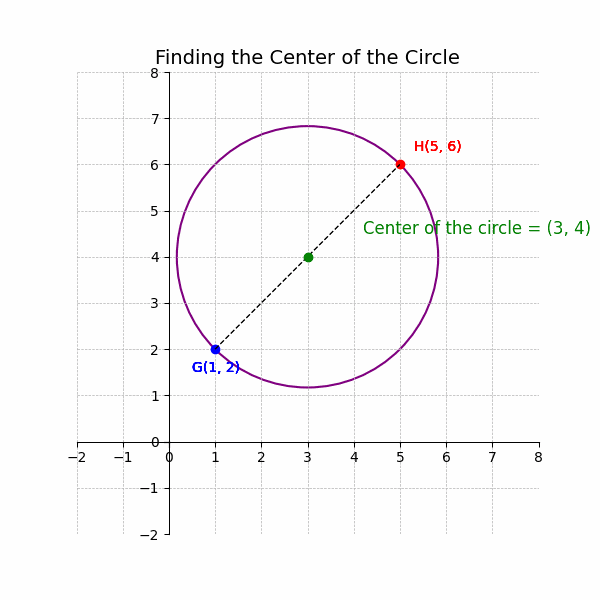
One of the most common applications is finding the center of a circle. If you know the endpoints of a diameter of a circle, the midpoint of that diameter is the center of the circle. This is because a diameter is a line segment that passes through the center of the circle and connects two points on the circumference. By using the Midpoint Formula, you can easily determine the coordinates of the circle’s center, which is crucial for calculating the circle’s radius, area, and circumference. This application demonstrates how the formula can be used to solve practical geometric problems.

Example: A circle has a diameter with endpoints G(1, 2) and H(5, 6). Find the center of the circle.

Solution:

1. Identify the coordinates: ##x_1 = 1, y_1 = 2, x_2 = 5, y_2 = 6##

2. Apply the formula:

##x_m = \frac{1 + 5}{2} = \frac{6}{2} = 3##

##y_m = \frac{2 + 6}{2} = \frac{8}{2} = 4##

3. Calculate the Midpoint: The center of the circle is (3, 4).

4. Write the Result: The center of the circle is (3, 4).

Determining the Centroid of a Triangle

The centroid of a triangle is the point where the three medians of the triangle intersect. A median is a line segment that connects a vertex of the triangle to the midpoint of the opposite side. To find the centroid, you first need to find the midpoints of the sides of the triangle using the Midpoint Formula. Then, you can use these midpoints to determine the centroid. The centroid is also known as the center of gravity of the triangle. This application showcases how the Midpoint Formula is used in more complex geometric constructions.

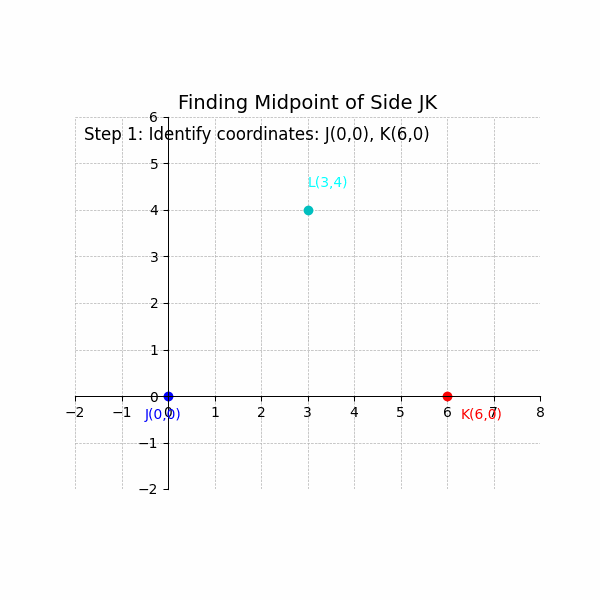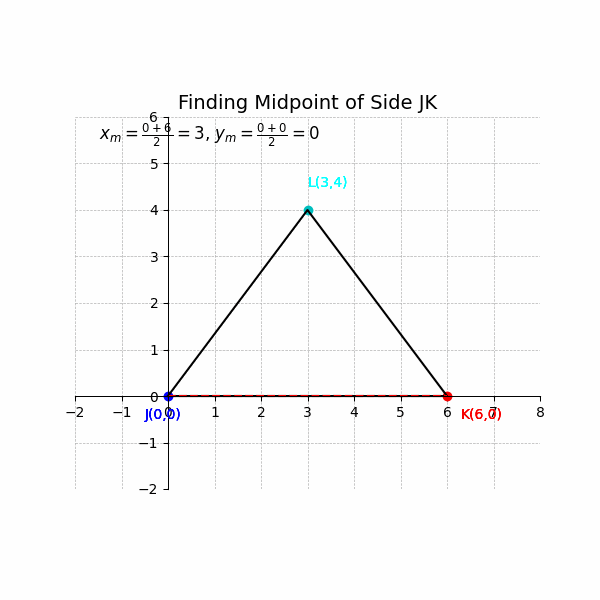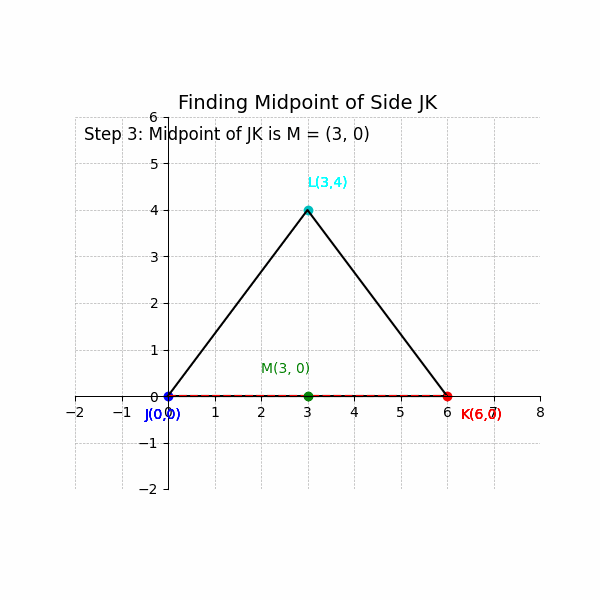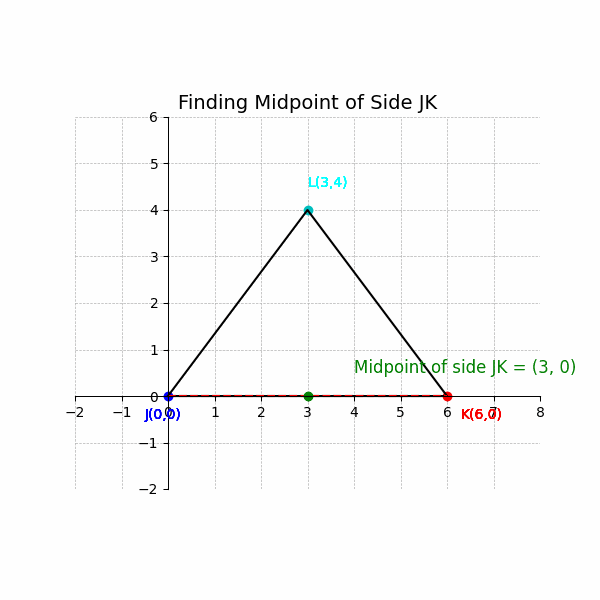
Example: A triangle has vertices J(0, 0), K(6, 0), and L(3, 4). Find the midpoint of side JK.

Solution:

1. Identify the coordinates: ##x_1 = 0, y_1 = 0, x_2 = 6, y_2 = 0##

2. Apply the formula:

##x_m = \frac{0 + 6}{2} = \frac{6}{2} = 3##

##y_m = \frac{0 + 0}{2} = \frac{0}{2} = 0##

3. Calculate the Midpoint: The midpoint is (3, 0).

4. Write the Result: The midpoint of the side JK is (3, 0).

Practice Problems on Midpoint Formula

To solidify your understanding, let’s work through some practice problems. These problems will help you apply the Midpoint Formula in various scenarios and build your confidence.

Problem 1

Find the midpoint of the line segment with endpoints A(3, 7) and B(9, 1).

Solution:

1. Identify the coordinates: ##x_1 = 3, y_1 = 7, x_2 = 9, y_2 = 1##

2. Apply the formula:

##x_m = \frac{3 + 9}{2} = \frac{12}{2} = 6##

##y_m = \frac{7 + 1}{2} = \frac{8}{2} = 4##

3. Calculate the Midpoint: The midpoint is (6, 4).

4. Write the Result: The midpoint of the line segment AB is (6, 4).

Problem 2

Find the midpoint of the line segment with endpoints C(-2, 5) and D(4, -3).

Solution:

1. Identify the coordinates: ##x_1 = -2, y_1 = 5, x_2 = 4, y_2 = -3##

2. Apply the formula:

##x_m = \frac{-2 + 4}{2} = \frac{2}{2} = 1##

##y_m = \frac{5 + (-3)}{2} = \frac{2}{2} = 1##

3. Calculate the Midpoint: The midpoint is (1, 1).

4. Write the Result: The midpoint of the line segment CD is (1, 1).

Problem 3

Find the midpoint of the line segment with endpoints E(1/4, 6) and F(7/4, 2).

Solution:

1. Identify the coordinates: ##x_1 = 1/4, y_1 = 6, x_2 = 7/4, y_2 = 2##

2. Apply the formula:

##x_m = \frac{1/4 + 7/4}{2} = \frac{8/4}{2} = \frac{2}{2} = 1##

##y_m = \frac{6 + 2}{2} = \frac{8}{2} = 4##

3. Calculate the Midpoint: The midpoint is (1, 4).

4. Write the Result: The midpoint of the line segment EF is (1, 4).

More Practice Problems

Here are a few more problems to test your understanding of the Midpoint Formula. Try solving these on your own and then check your answers.

Problem 4

Find the midpoint of the line segment with endpoints G(0, -4) and H(6, 0).

Solution: (3, -2)

Problem 5

Find the midpoint of the line segment with endpoints I(-5, -1) and J(1, 3).

Solution: (-2, 1)

Problem 6

Find the midpoint of the line segment with endpoints K(2.5, 3.5) and L(5.5, 6.5).

Solution: (4, 5)