Welcome to the fascinating world of conic sections! This lesson focuses on ellipses, a fundamental shape in geometry with numerous applications in science, engineering, and everyday life. Understanding ellipses is crucial for anyone studying coordinate geometry. We will explore the definition, properties, equations, and applications of ellipses in detail.

What is an Ellipse?

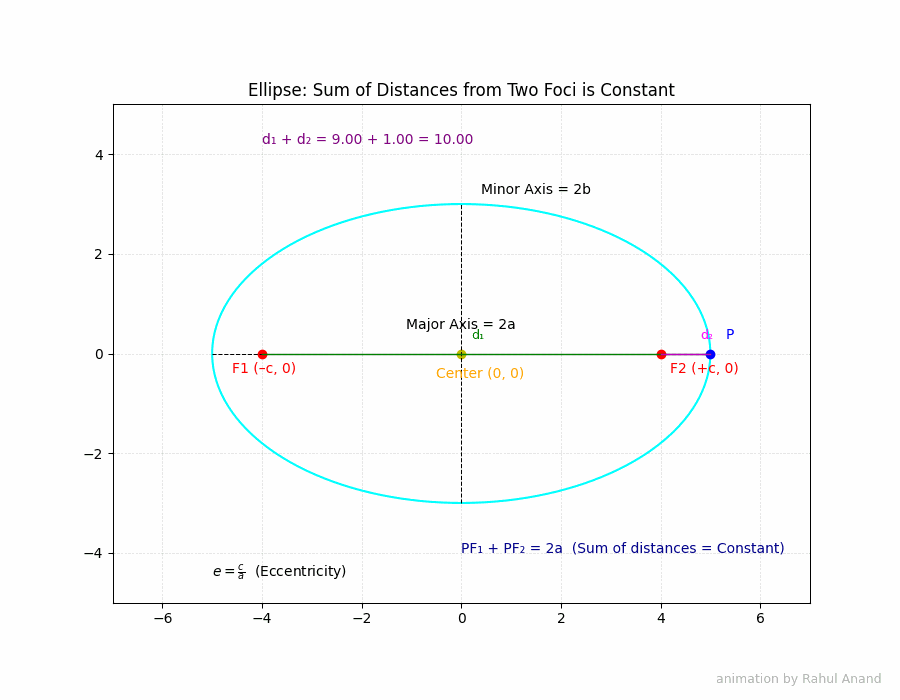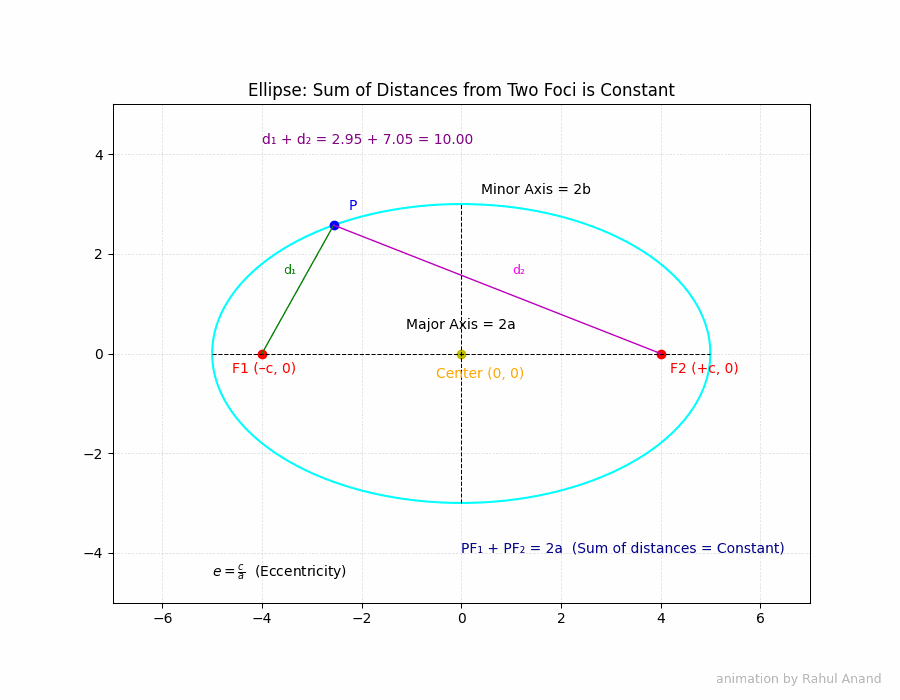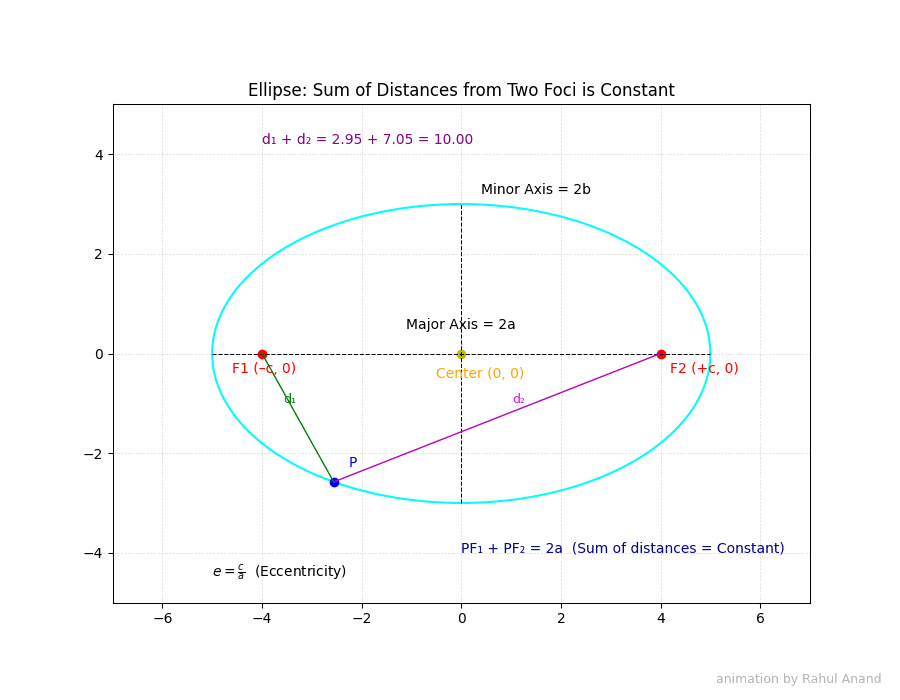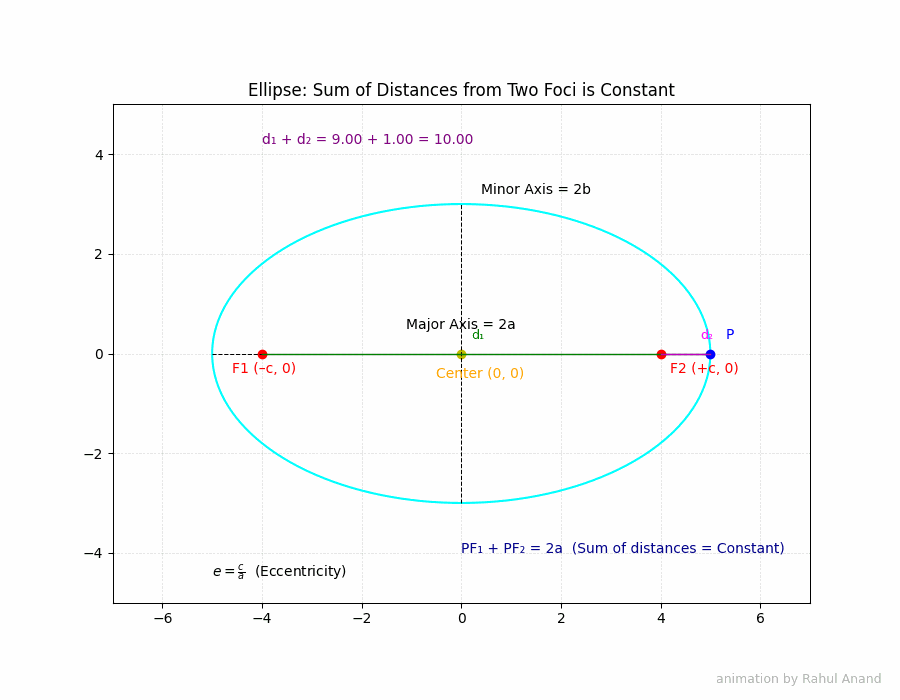
An ellipse is a closed curve formed by the intersection of a cone and a plane that is not parallel to the base, axis, or a generator of the cone. More formally, an ellipse is the set of all points in a plane such that the sum of the distances from two fixed points (called foci) to any point on the curve is constant.

Let’s break down this definition:

• Foci (plural of focus): These are two fixed points inside the ellipse.
• Constant Sum: For any point on the ellipse, the sum of its distances to the two foci is always the same.

Imagine a string tied at two points (the foci). If you use a pencil to pull the string taut and trace around, you’ll create an ellipse. The length of the string represents the constant sum of distances.

Key Properties of an Ellipse

Before diving into equations, let’s understand the key components and properties of an ellipse. These are essential for understanding and working with ellipses.

• Center: The midpoint of the segment connecting the two foci.
• Vertices: The points on the ellipse that are farthest from the center. An ellipse has two vertices.
• Major Axis: The line segment passing through the foci and the vertices. Its length is 2a, where a is the distance from the center to a vertex.
• Minor Axis: The line segment perpendicular to the major axis, passing through the center, and intersecting the ellipse at two points. Its length is 2b, where b is the distance from the center to a point on the minor axis.
• Focal Length (c): The distance from the center to each focus. The relationship between a, b, and c is given by ##c^2 = a^2 – b^2##.
• Eccentricity (e): A measure of how “stretched” an ellipse is. It’s defined as ##e = \frac{c}{a}##. The eccentricity is always between 0 and 1. A circle has an eccentricity of 0, and as the ellipse becomes more elongated, the eccentricity approaches 1.

Let’s visualize these properties. Consider an ellipse centered at the origin (0, 0):

Imagine an ellipse with foci F1 and F2. Let P be any point on the ellipse. Then, by definition, the sum of the distances PF1 + PF2 is constant. This constant is equal to 2a, the length of the major axis.

I have animated the above facts in the figure above for reference. I hope you will find it helpful.

Our next topic of discussion will be mathematical equations describing ellipses in Standard Equations of an Ellipse.

---