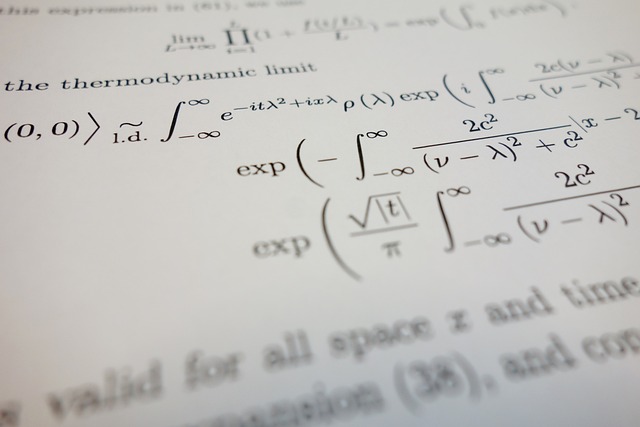Discover the top AI tools to boost your productivity and efficiency. Learn about various AI tools.
Featured Articles on: SETS
Can Subsets of Natural Numbers Have Equal Harmonic Series Sums?
Explore if disjoint subsets of natural numbers exist where the sum of harmonic series terms over each subset is equal. Investigate the harmonic series and its subset sums.
Finding Subsets of Natural Numbers with Equal Sums of Reciprocals of Squares
Discover how to find subsets of natural numbers where the sum of reciprocals of their squares is equal exploring both finite and infinite cases.
New Types of Infinity Challenge Traditional Views in Set Theory
Discover exacting and ultraexacting cardinals new types of infinity challenging traditional set theory views and potentially resolving long-standing conjectures.
Understanding Sophie Germain Primes: Properties Applications and Algorithms
Discover Sophie Germain primes special prime numbers with unique properties. Learn about their relation to safe primes applications in cryptography and how to identify them using Python.
Understanding Vectors in Mathematics: Definition Operations and Applications
Learn about vectors in mathematics their properties and how they’re used in physics computer graphics and machine learning.
Proving Mathematical Propositions: Direct Indirect and Other Methods
Learn various methods for proving mathematical statements including direct proof indirect proof (contradiction and contrapositive) proof by cases and mathematical induction. Explore examples and applications.
Navigating the CBSE Board Exams 2025: A Comprehensive Guide
Conquer the CBSE Board Exams 2025 with our guide! Learn effective study strategies, time management tips, and overcome exam anxiety for success.
De Morgan’s laws
De Morgan’s First Law The complement of the union of two sets is equal to the intersection of their complements i.e. (A ∪ B )' = A' ∩ B' De Morgan’s Second Law The complement of the intersection of two sets is equal to the union of their complements i.e. (A ∩ B )’ =...
Cartesian Product of Sets
A cartesian product between two sets is defined as the set consisting of all possible ordered pairs that can be formed by taking one element from each of the sets at a given time. If A and B are two sets such that a ∈ A and b ∈ B, then the cartesian product between A...
Ordered Pairs
An ordered pair is a 2-tuple formed by taking two elements (generally numbers but can be alphabets, characters, words, or symbols). The general form of representation is (a, b) where a and b represent two distinct objects. The important thing with ordered pairs is...
Cartesian Product
The cartesian product of two sets A and B is defined as a set formed by all the possible ordered pairs of elements from A and B, such that the first element comes from set A and the second element comes from set B. The cartesian product is denoted as A × B....
Intersection operation on two sets
The intersection of two sets A & B is defined as a set that contains only those members which are common to both A and B. The intersection operation is denoted by the symbol ∩. Remember, for two disjoint sets (sets having no common elements), the...
Union of two sets
The union of two sets A & B is defined as a set that contains all the member elements of A and B. the union operation is denoted by the symbol ∪. One point to remember here is that the union of two or more sets always gives a set with distinct...
Complement of a set
The complement of a set A (that is a subset of a universal set U) is defined as a set that contains all the member elements and all subsets of U that are not part of the set A. The complement of a set is denoted using the symbol ‘ or c. Hence, A’ =...
Venn Diagrams in Sets
Venn diagrams are the pictorial or graphical representation of sets and the various relationships that exist between sets. The representation consists of a rectangular box representing the universal set(U). All sets that are in context are drawn as circles...