Explore how function behavior changes with large variables. Learn to identify warning signs and avoid common pitfalls in mathematical analysis.
Unpredictable Function Behavior: Exploring Large Variables
read more
Category Archives
RELATIONS & FUNCTIONS
Recent Articles in Mathematics
Prove Bounded Function
Learn how to prove that a function is bounded with this step-by-step guide. Master the techniques for a bounded function proof.
Unfolding Functions: Exploring Compositional Square Roots
Discover which functions have compositional square roots! Learn about bijections, cycle decomposition, and how to find these roots.
Divisibility by Floor Square Root: A Number Theory Problem
Explore the divisibility by floor square root problem. Find all integers ##n## where ##\lfloor{\sqrt{n}}\rfloor \mid n##. Solutions and examples included.
Fuzzy Logic Aggregation Techniques
Learn fuzzy logic aggregation techniques to combine uncertain data. Enhance decision-making and risk assessment with fuzzy values.
Understanding Derivatives Simply: A Beginner’s Guide
Understanding derivatives simply involves grasping how functions change. This guide offers an intuitive explanation for beginners.
Understanding the Ramp Function: Definition and Applications
Explore the ramp function, its definition, properties, and applications in signal processing and control systems. Understand the ramp function today!
Surjective Function Composition: Explained with Examples
Explore surjective function composition with clear examples. Learn when the composition of surjective functions remains surjective and when it doesn’t.
Demystifying Function Codomain: Definition and Importance
Explore the function codomain, its definition, and why it’s crucial in math. Understand its role in function composition and surjectivity.
Function Decomposition: Even and Odd Parts
Learn how to perform function decomposition by separating any function into its even and odd parts, simplifying complex analysis.
Proving Independence of n: A Number Theory Challenge
Prove that an expression is independent of n using number theory. Explore modular arithmetic and floor functions to show constant results.
Arc Length Functions: A Deep Dive
Explore arc length functions and their cardinality. Discover how the number of continuous functions changes with increasing arc length.
Defining Integrals: Key Conditions Explained
Explore the conditions for defining integrals, focusing on the necessary structures of spaces and functions for meaningful integration.
Understanding P-Value Variance: The x(1-x) Function
Explore the meaning of p-value variance, ##x(1-x)##, in statistics. Learn how it relates to Bernoulli distribution and its applications.
Crossfader Curves: Formulas and DJ Techniques
Explore the formulas behind common crossfader curves like Dipped, Constant Power, and Linear. Enhance your DJ mixing skills today!
Understanding L-Structures: First-Order Logic Explained
Explore L-structures in first-order logic, their construction, and counting methods. Understand how L-structures first order logic works with examples.
Solving Function Composition Problems Algebraically
Learn how to solve function composition problems algebraically with step-by-step solutions. Master the art of decomposing complex functions!
Area of Recursive Functions: A Detailed Analysis
Explore the area of recursive functions with a detailed analysis. Discover how the area remains constant as the recursion depth increases.
Understanding Function Sections
Explore function sections, a method to simplify multi-variable functions by fixing one variable. Learn how function sections aid in analysis.
Function Iteration Notation
Explore function iteration notation with clear examples. Learn how to represent repeated function compositions effectively and avoid common ambiguities.
Understanding Function Decay Rates: Slow vs. Rapid
Explore function decay rates and how the parameter α affects whether a function has slow or rapid decay. Learn with examples!
Representing Logical Operators as Functions
Learn how to represent logical operators like AND, OR, and NOT as functions. Understand their mathematical formulations and applications.
Constructing Continuous Functions: Examples and Proofs
Learn how to build functions continuous at specific points, like integers or irrationals. Explore examples and proofs for constructing continuous functions.
Understanding ##\Theta## Complexity: Proving Floor Function’s Growth
Explore proving that the floor function has Theta complexity of Θ(x). Learn about upper and lower bounds in this analysis.
Summing Hadamard Product of Generating Functions
Learn how to efficiently compute the sum of coefficients in the Hadamard product of generating functions. Simplify complex calculations!
Function Notation Explained: f(x) vs. f
Understanding function notation is key! Learn the difference between f(x) and f, and how to use them correctly in math.
Fractional Differentiability of Functions
Explore fractional differentiability functions and how they behave with non-integer derivatives. Learn about constructing functions with specific differentiability.
Generalized Cosine Functions and Equations
Explore generalized cosine functions through functional equations. Understand solutions and challenges in higher-order generalizations.
Finding Minimum Value Function
Learn how to find the minimum value function using calculus. Step-by-step guide included!
Density of Smooth Functions in L1 and L2 Spaces
Explore the density of smooth functions in L1 and L2 spaces. Learn how smooth functions approximate complex functions effectively.
Diagonal Tiling of Piecewise Functions
Learn how to tile piecewise functions diagonally across a grid. This guide provides a clear solution for transforming inputs and achieving the desired tiling effect.
Unveiling the Mandelbrot Set Main Cardioid
Explore the Mandelbrot set main cardioid, its fixed points, and multipliers. Understand its role in complex dynamics and the Mandelbrot set.
Unlocking the Secrets of Prime Numbers
Explore the definition, identification, and applications of prime numbers. Understand why prime numbers are crucial in cryptography and computer science.
Unveiling Expected Rolls: Dice Probability Explained
Explore the probability of expected rolls to see all sides of a die. Understand why multiple dice don’t simply halve the expectation.
Understanding Ordered Pairs: Definition Examples and Applications
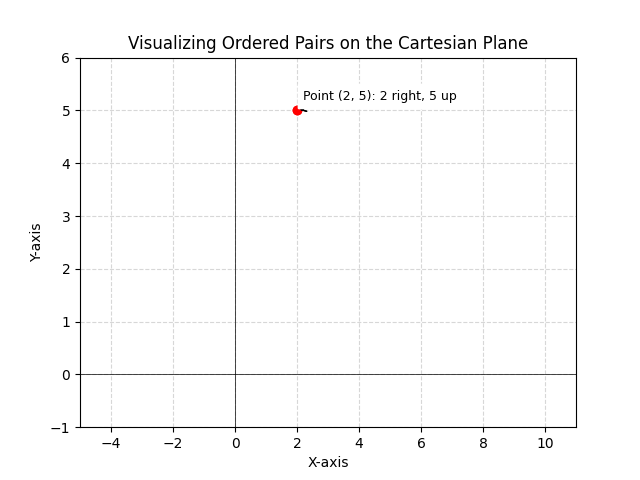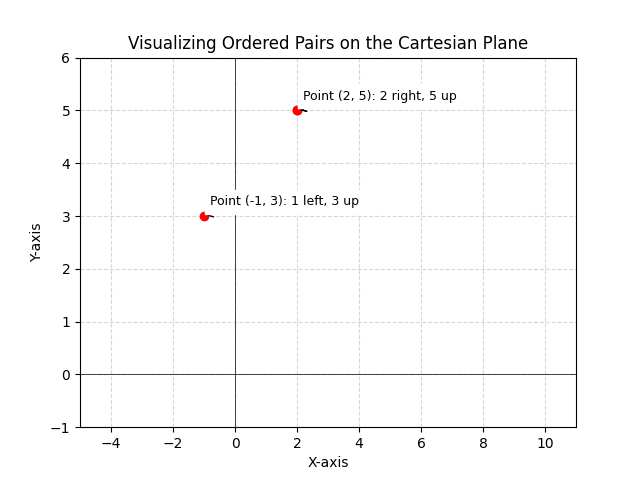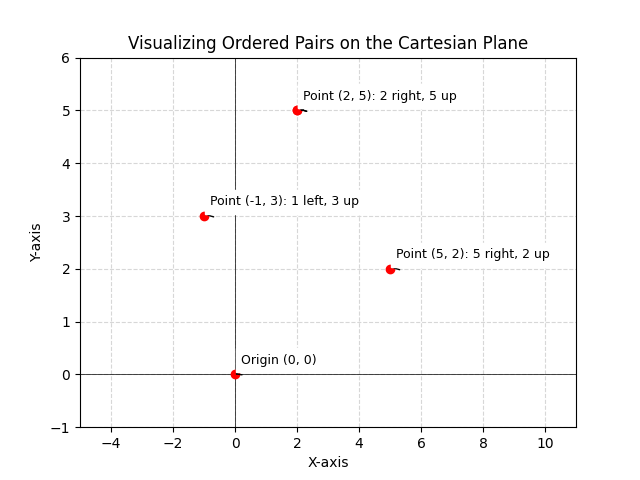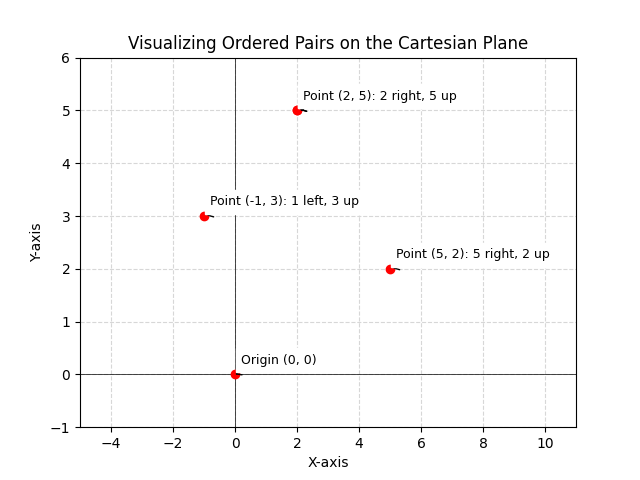
Learn the definition of an ordered pair in mathematics including its key characteristics and applications. Explore examples and understand how it’s used.
Solving Polynomial Equations: Finding q(uv) = 0
Discover how to solve polynomial equations and find q(uv) = 0. Learn techniques for determining polynomial relationships between variables. Polynomial Equation Solver.
What are the Best AI Tools for Your Needs?
Discover the top AI tools to boost your productivity and efficiency. Learn about various AI tools.
Understanding Sequences and Limits: A Comprehensive Guide
Learn about sequences their limits and how they differ from functions. Discover convergence and divergence and essential theorems.
Understanding Arithmetic Geometric and Harmonic Series: 5 Examples Each
Learn about arithmetic geometric and harmonic series with 5 examples each. Discover the formulas and how to solve problems.
Understanding Sophie Germain Primes: Properties Applications and Algorithms
Discover Sophie Germain primes special prime numbers with unique properties. Learn about their relation to safe primes applications in cryptography and how to identify them using Python.
Solving the Surjective Function Equation f(x) for Positive Real Numbers
Discover the surjective functions f(x) that satisfy the equation 2xf(f(x)) = f(x)(x + f(f(x))) for all positive real numbers x.
Solving Functional Equations: Finding f(x) and g(x)
Discover how to find functions f(x) and g(x) that satisfy a specific functional equation. Explore different cases and solutions.
Solving Surjective Functions: A Functional Equation Approach
Discover how to find all surjective functions f:R→R satisfying a specific functional equation. Learn the key steps and techniques.
Solving Functional Equations: Tips and Tricks for Midterm Prep
Struggling with functional equations for your math midterm? This post provides tips and tricks including substituting values using mathematical induction and finding fixed points to help you solve these challenging problems.
Understanding Vectors in Mathematics: Definition Operations and Applications
Learn about vectors in mathematics their properties and how they’re used in physics computer graphics and machine learning.
Proving Mathematical Propositions: Direct Indirect and Other Methods
Learn various methods for proving mathematical statements including direct proof indirect proof (contradiction and contrapositive) proof by cases and mathematical induction. Explore examples and applications.
Navigating the CBSE Board Exams 2025: A Comprehensive Guide
Conquer the CBSE Board Exams 2025 with our guide! Learn effective study strategies, time management tips, and overcome exam anxiety for success.
Cartesian Product
The cartesian product of two sets A and B is defined as a set formed by all the possible ordered pairs of elements from A and B, such that the first element comes from set A and the second element comes from set B. The cartesian product is denoted as A × B. ​Let a and...
Ordered Pairs
An ordered pair is a 2-tuple formed by taking two elements (generally numbers but can be alphabets, characters, words or symbols). The general form of representation is (a, b) where a and b represent two distinct objects. The important thing with ordered pairs is that...
Tuples
Tuples in Relations and their examples
Relations & Sets
A Relation from set A to set B is defined as a set of ordered pairs formed from the elements of set A and B. In other words, a relation is a subset of the cartesian product of sets A and B. The subset is derived by establishing predicate filter(s) or criteria stating...
Even & Odd FunctionsÂ
A function is said to be an even function if the sign of the image does not change when the sign of the preimage changes. Conversely, a function is called an odd function when the sign of the image changes when the sign of the preimage changes. For Even functions,...
Tuples
In mathematics, a tuple or a sequence is a list of objects arranged in an order. Such a list may have repeated objects but the order is more important. Such sequences or tuples are denoted as ( t1, t2, t3, …., tn ) where tn is the nth element of the list. Below are a...