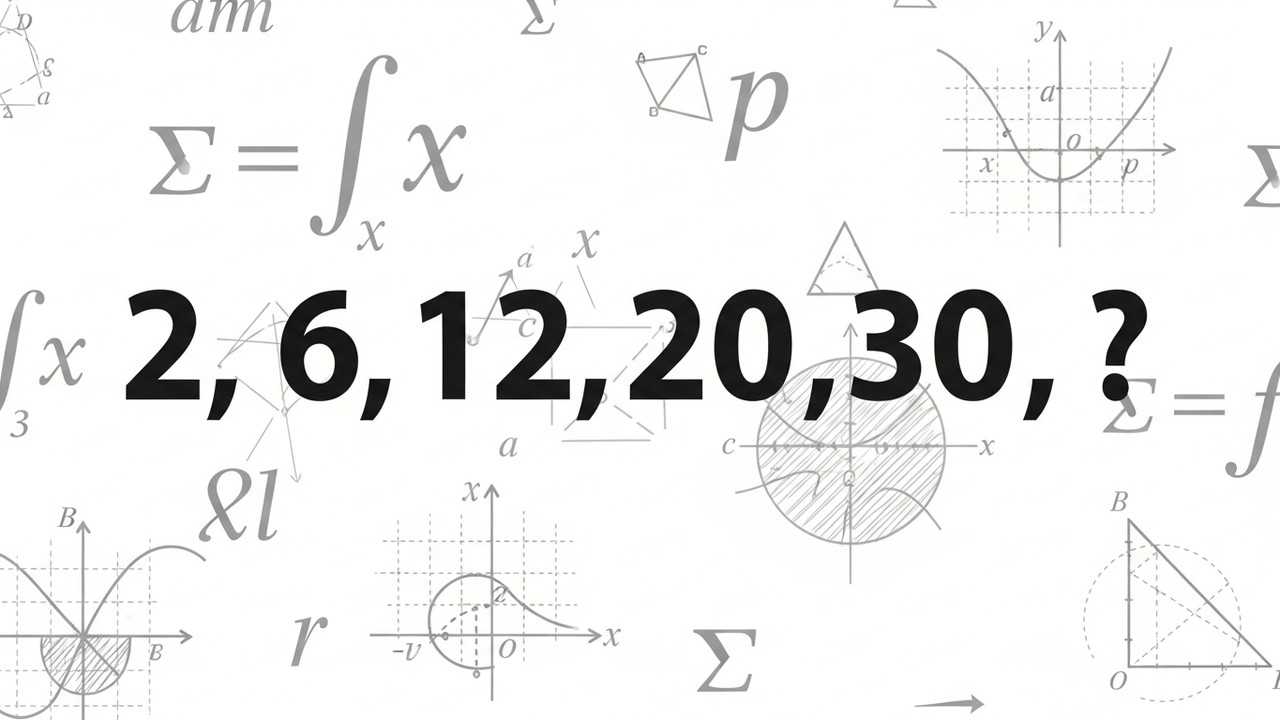Master the STEM-Quant Module GRE with our comprehensive guide. Explore technical details, strategic benefits, and how this optional add-on helps engineering applicants stand out for MIT, Stanford, and beyond.
Featured Articles on: SERIES AND SEQUENCES
Infinite Geometric Series: Detailed Solution and Convergence Analysis
A comprehensive technical guide to solving infinite geometric series with detailed proofs, step-by-step arithmetic, and historical context.
The Power of Banach Limits
Explore the fascinating world of the Banach Limit, a mathematical tool that extends the concept of limits beyond convergent sequences, assigning a limit value to sequences that might otherwise seem ‘limitless’.
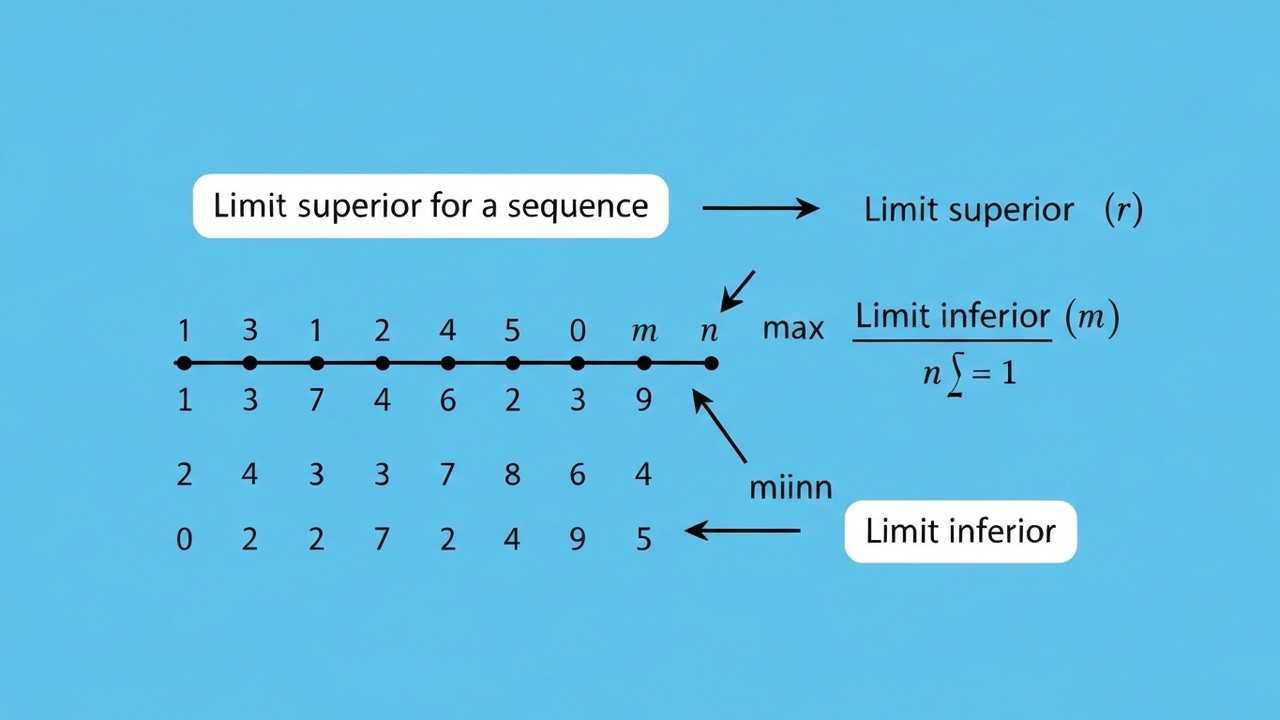
Limit Superior and Inferior
Understand Limit Superior and Inferior: Learn how these concepts define the eventual bounds of sequences and functions, and their importance in mathematical analysis.
The Diverse Types of Convergence in Mathematics
Understanding the different **types of convergence** is essential in mathematics. From sequences and series to functions, this post explores the various modes of convergence.
Average of Five Numbers Problem with One Removed
Averages are tested often in aptitude exams with practical twists.
Find the Missing Term in the Series 2, 6, 12, 20, 30
Number series problems improve pattern recognition for competitive exams.
The Sum of Series Formula
This post explores the Sum of Series Formula, showing you how to derive and apply it to solve complex series problems. You’ll learn the formula and see examples.
Unpredictable Function Behavior: Exploring Large Variables
Explore how function behavior changes with large variables. Learn to identify warning signs and avoid common pitfalls in mathematical analysis.
Prove Bounded Function
Learn how to prove that a function is bounded with this step-by-step guide. Master the techniques for a bounded function proof.
Fuzzy Logic Aggregation Techniques
Learn fuzzy logic aggregation techniques to combine uncertain data. Enhance decision-making and risk assessment with fuzzy values.
Function Decomposition: Even and Odd Parts
Learn how to perform function decomposition by separating any function into its even and odd parts, simplifying complex analysis.
Proving Independence of n: A Number Theory Challenge
Prove that an expression is independent of n using number theory. Explore modular arithmetic and floor functions to show constant results.
Arc Length Functions: A Deep Dive
Explore arc length functions and their cardinality. Discover how the number of continuous functions changes with increasing arc length.
Defining Integrals: Key Conditions Explained
Explore the conditions for defining integrals, focusing on the necessary structures of spaces and functions for meaningful integration.
Solving Function Composition Problems Algebraically
Learn how to solve function composition problems algebraically with step-by-step solutions. Master the art of decomposing complex functions!