In a 2026 breakthrough, Terence Tao uses Aristotle AI and Lean 4 to solve the Erdős-Herzog-Piranian lemniscate conjecture. Explore the technical details of this AI-math collaboration.
Featured Articles on: FUNCTIONS
Masaki Kashiwara 2026: Closing the Analysis-Topology Gap
Explore Masaki Kashiwara’s groundbreaking 2026 paper on the Riemann-Hilbert correspondence, D-modules, and its impact on quantum technology and mathematical physics.
Functional Equations: Solving f(x+y) = f(x) + f(y) + 2xy
A technical analysis and step-by-step solution for the advanced functional equation f(x+y) = f(x) + f(y) + 2xy with the boundary condition f(1) = 2.
Functional Equations: Solving ##f(x+y) = f(x) + f(y) + 2xy##
Technical Specifications and Variable Analysis Formal Problem Definition The mathematical operation under investigation involves a classic challenge in Logarithmic Equation Solving where the primary variable is embedded within multiple transcendental terms. We are taske…
Simplify ## \frac{x^2 – 9}{x^2 + 5x + 6} ##
Learn how to simplify ##\frac{x^2 – 9}{x^2 + 5x + 6}## using difference of squares and trinomial factoring while identifying excluded values and discontinuities.
The Power of Banach Limits
Explore the fascinating world of the Banach Limit, a mathematical tool that extends the concept of limits beyond convergent sequences, assigning a limit value to sequences that might otherwise seem ‘limitless’.
The Diverse Types of Convergence in Mathematics
Understanding the different **types of convergence** is essential in mathematics. From sequences and series to functions, this post explores the various modes of convergence.
Evaluating Limits Problems: Step-by-Step Solutions
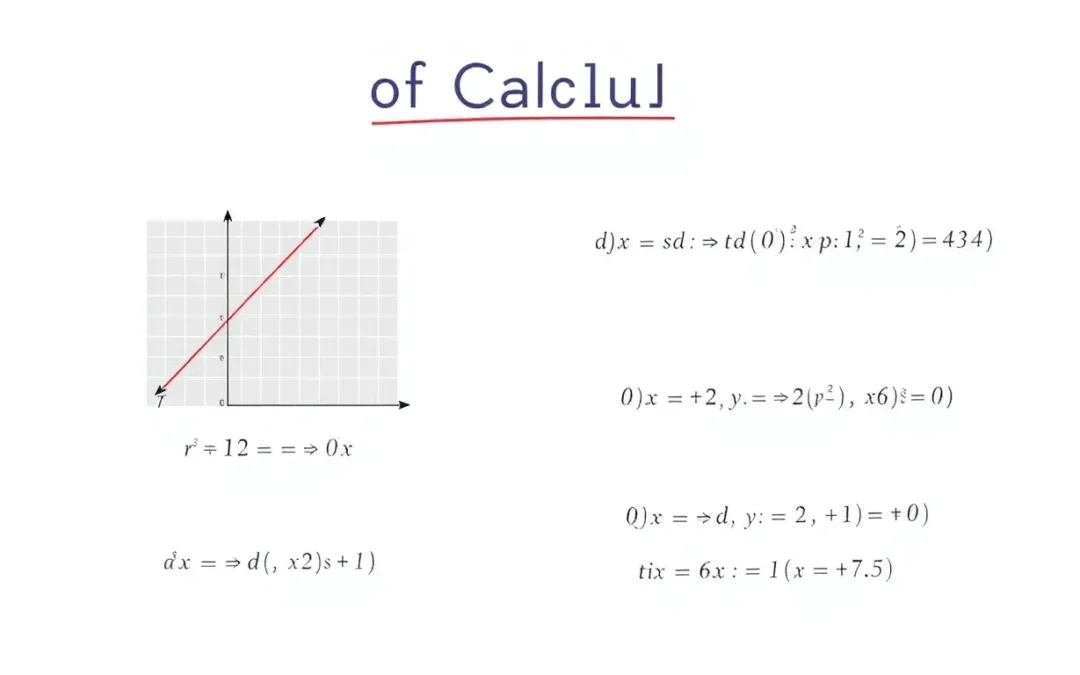
Learn how to solve Evaluating Limits Problems with this step-by-step guide. We’ll cover the fundamentals and provide clear examples.
Understanding Limits by Factorization
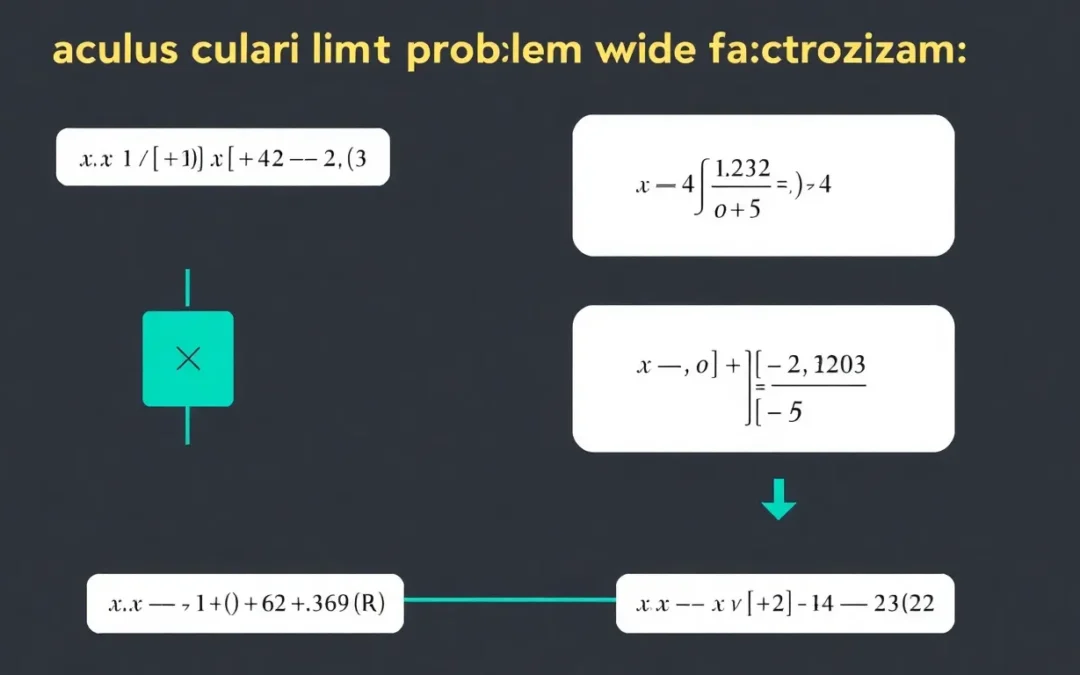
Learn to solve limits that result in indeterminate forms using **Limits by Factorization**. This method simplifies the expression to find the value the function approaches.
Unpredictable Function Behavior: Exploring Large Variables
Explore how function behavior changes with large variables. Learn to identify warning signs and avoid common pitfalls in mathematical analysis.
Prove Bounded Function
Learn how to prove that a function is bounded with this step-by-step guide. Master the techniques for a bounded function proof.
Unfolding Functions: Exploring Compositional Square Roots
Discover which functions have compositional square roots! Learn about bijections, cycle decomposition, and how to find these roots.
Divisibility by Floor Square Root: A Number Theory Problem
Explore the divisibility by floor square root problem. Find all integers ##n## where ##\lfloor{\sqrt{n}}\rfloor \mid n##. Solutions and examples included.
Fuzzy Logic Aggregation Techniques
Learn fuzzy logic aggregation techniques to combine uncertain data. Enhance decision-making and risk assessment with fuzzy values.
Understanding Derivatives Simply: A Beginner’s Guide
Understanding derivatives simply involves grasping how functions change. This guide offers an intuitive explanation for beginners.
Understanding the Ramp Function: Definition and Applications
Explore the ramp function, its definition, properties, and applications in signal processing and control systems. Understand the ramp function today!