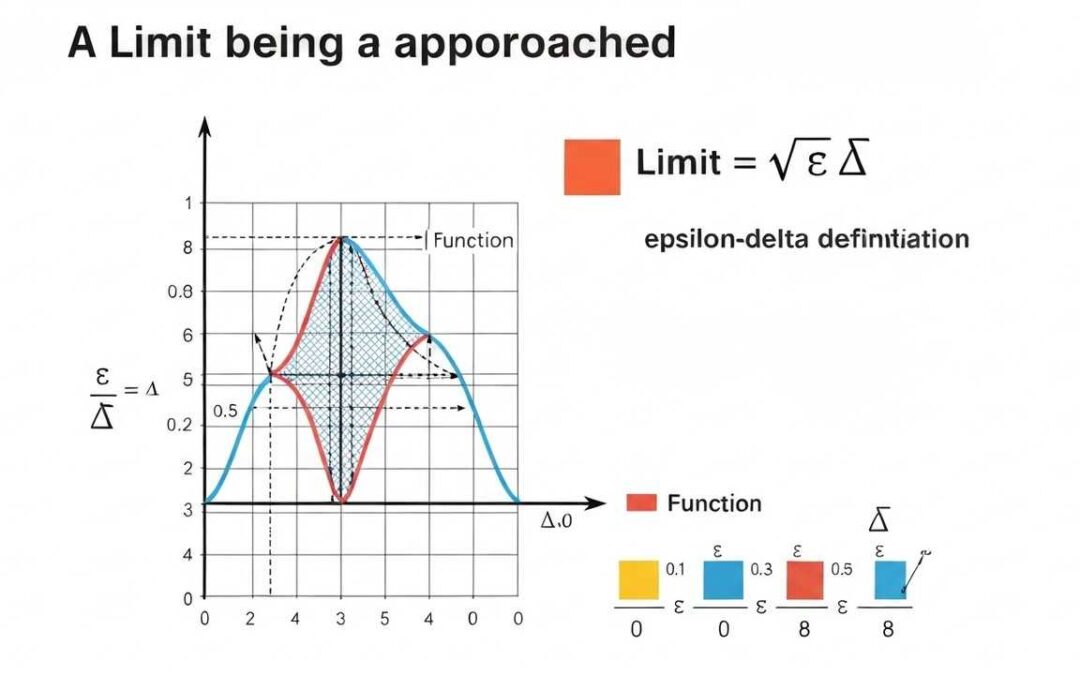
Understanding **limits of functions** is essential in calculus. This guide explains the epsilon-delta definition, theorems, and applications to help you master this fundamental concept.
Limits of Functions: A Complete Guide
read more
Category Archives
DIFFERENTIATION
Recent Articles in Mathematics
Limits: The Squeeze Theorem Explained
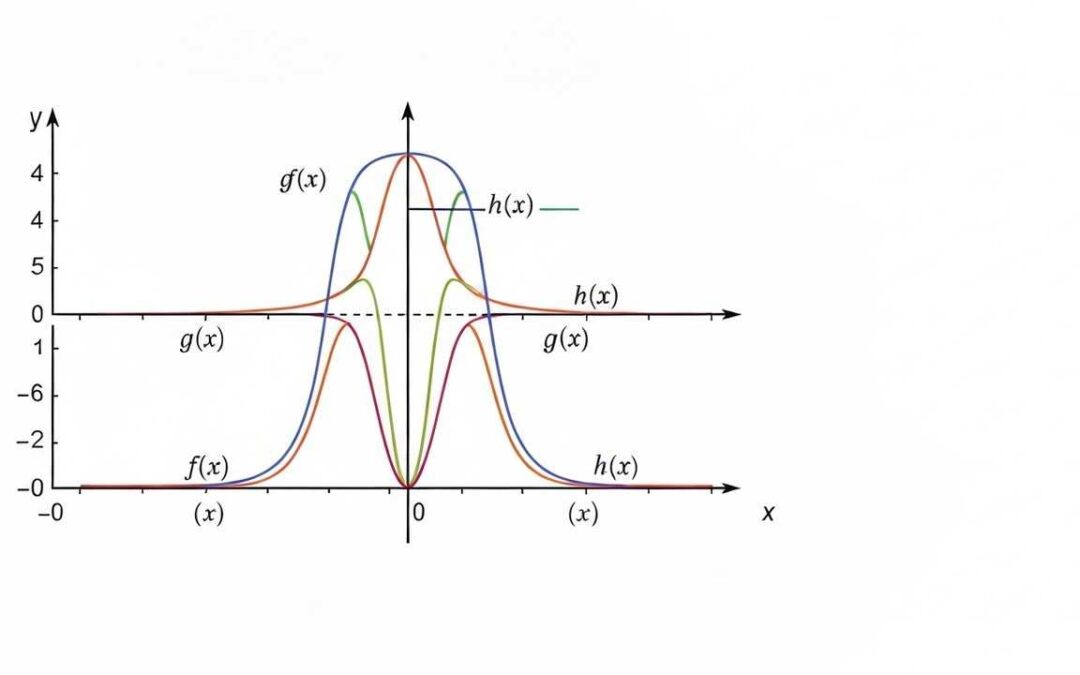
The Squeeze Theorem is a calculus concept that uses bounding functions to determine the limit of a function. The article explains how it works and provides examples.
Limit Superior and Inferior
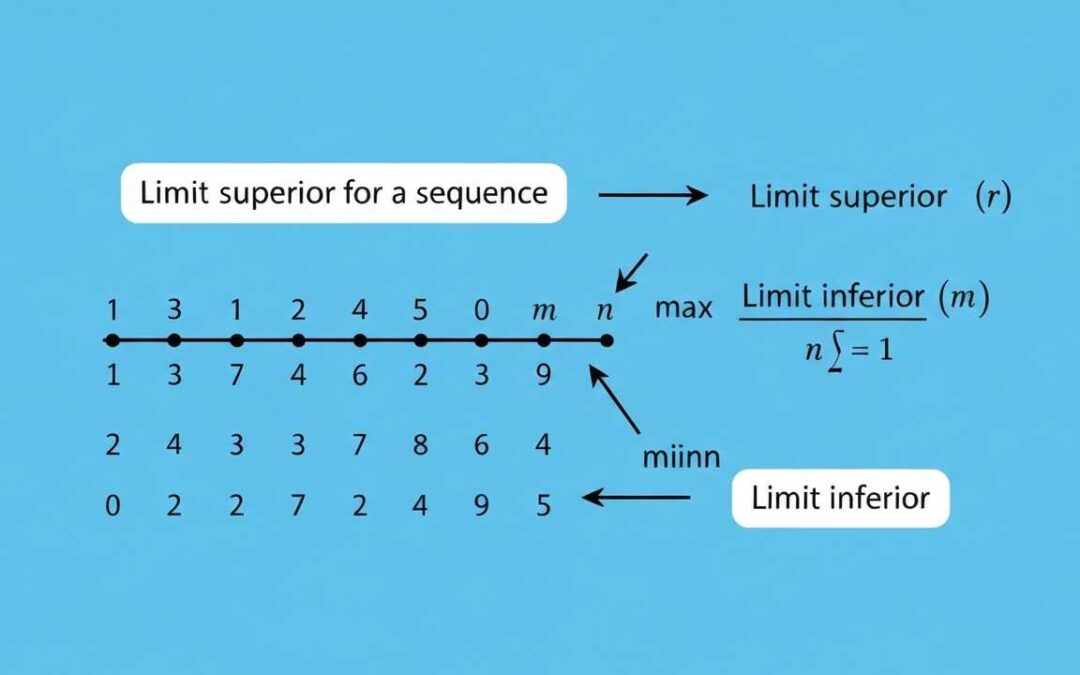
Understand Limit Superior and Inferior: Learn how these concepts define the eventual bounds of sequences and functions, and their importance in mathematical analysis.
Evaluating Limits Problems: Step-by-Step Solutions
Learn how to solve Evaluating Limits Problems with this step-by-step guide. We’ll cover the fundamentals and provide clear examples.
Limits at Infinity
Learn how to solve Limits at Infinity with this comprehensive guide. Understand the concepts and techniques through clear examples and step-by-step solutions.
Rationalizing Numerator Limits
Learn how to solve Rationalizing Numerator Limits by rationalizing the numerator to eliminate indeterminate forms and find the limit.
Trigonometric Limit
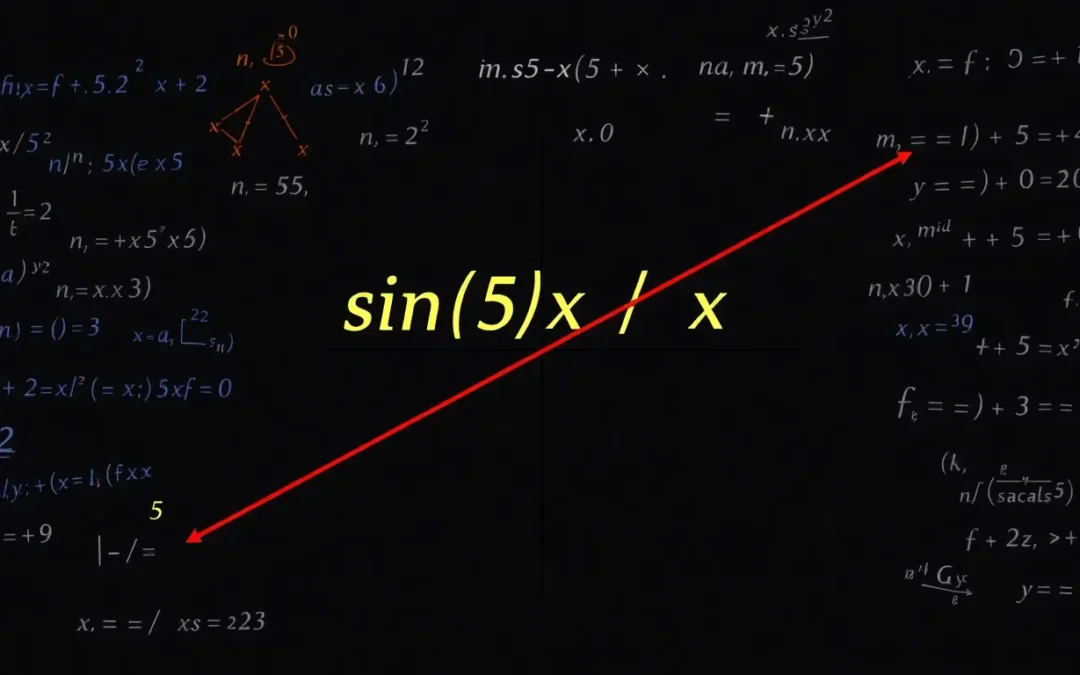
Learn to evaluate the Trigonometric Limit. The solution involves simplifying the expression and applying limit theorems. The final result is 5.
Understanding Limits by Factorization
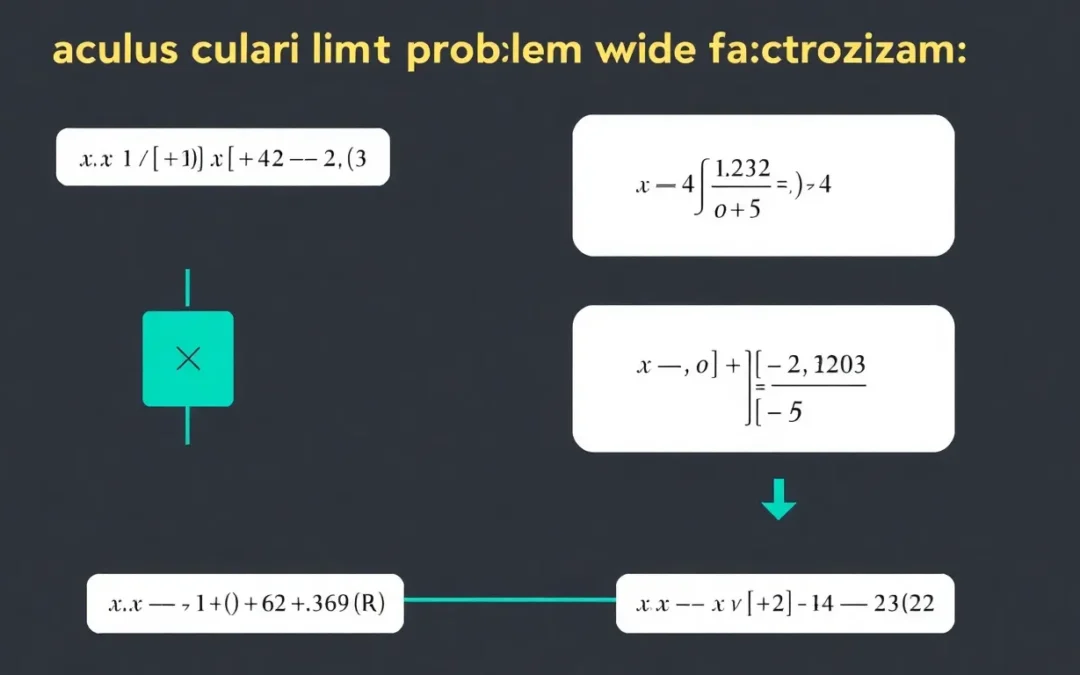
Learn to solve limits that result in indeterminate forms using **Limits by Factorization**. This method simplifies the expression to find the value the function approaches.
Evaluating Limits
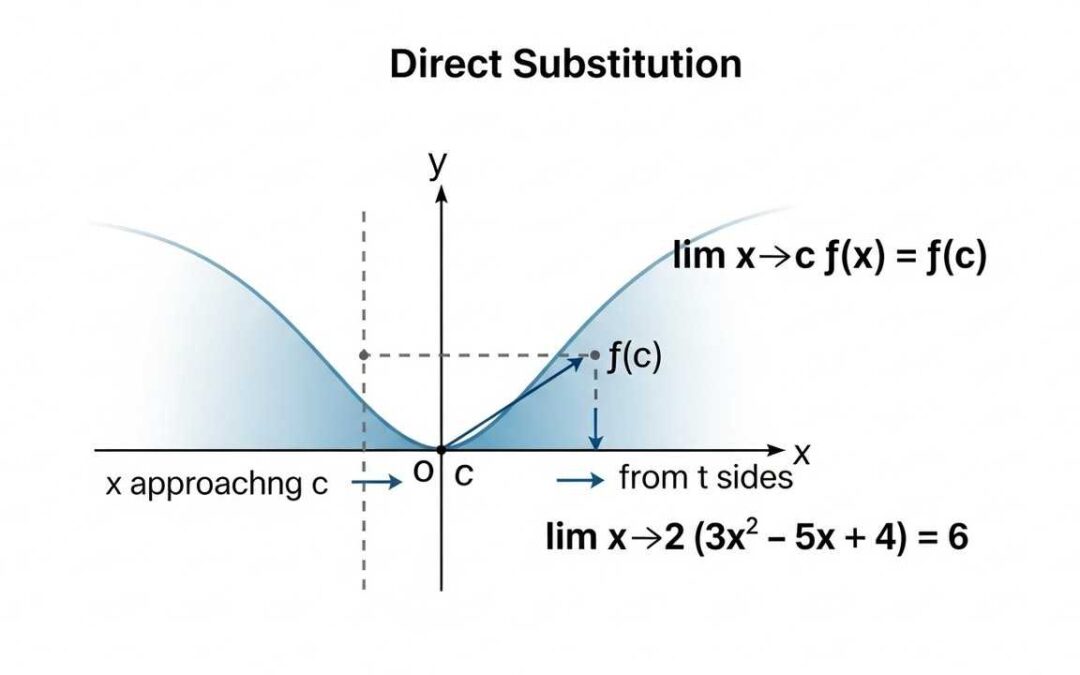
Learn how to easily evaluate limits using direct substitution! This guide provides clear examples and explanations to help you master this essential calculus skill. The SEO Keyphrase is Evaluating Limits.
Understanding Derivatives Simply: A Beginner’s Guide
Understanding derivatives simply involves grasping how functions change. This guide offers an intuitive explanation for beginners.
Fractional Differentiability of Functions
Explore fractional differentiability functions and how they behave with non-integer derivatives. Learn about constructing functions with specific differentiability.
Finding Minimum Value Function
Learn how to find the minimum value function using calculus. Step-by-step guide included!
Derivative of \(\mathsf { x^{n} }\) using the First Principle
Let y = \(\mathsf {x^{n} }\) ∴ y + δy = \(\mathsf { {(x + δx)^{n}} }\) ∴ δy = y + δy - y = \(\mathsf { (x + δx)^{n} }\) - \(\mathsf { x^{n} }\) or δy = \(\mathsf { [\text{ }^{n}C_0 x^{n}{(δx)}^{0} }\) + \(\mathsf {\text{ }^{n}C_1 x^{n-1}{(δx)}^{1}}\) + \(\mathsf...
Derivative of \({e}^x\) using First PrincipleÂ
Derivative of \({e}^x\) using the First Principle Let \(y\) = \({e}^x\)∴ \(y + δy\) = \({e}^{x + δx}\)∴ \(δy\) = \({e}^{x + δx}\) - \({e}^x\)or \(δy\) = \({e}^{x}\) . \( [ {e}^{δx} - 1 ]\)Dividing each side by δx </h3>or \(\dfrac {δy}{δx}\) = \( \dfrac { {e}^{x}...
Derivative of sinθ using the First Principle
Derivative of \( sinθ \) using the First Principle Let \(y\) = \( sinθ \) ∴ \(y + δy\) = \( sin(θ + δθ) \) ∴ \(δy\) = \( sin(θ + δθ) \) - \( sinθ \)From Trigonometry , we have \( sin(A-B) \) = 2.\( sin \dfrac {(A-B)}{2} \).\( cos \dfrac {(A+B)}{2} \)Using the above...
Derivative of cosθ using the First Principle
Derivative of \( cosθ \) using the First Principle Let \(y\) = \( cosθ \) ∴ \(y + δy\) = \( cos(θ + δθ) \) ∴ \(δy\) = \( cos(θ + δθ) \) - \( cosθ \)From Trigonometry , we have \( cos(A-B) \) = -2.\( sin \dfrac {(A+B)}{2} \).\( sin \dfrac {(A-B)}{2} \)Using the above...