The Stefan-Boltzmann law is a seminal principle underpinning the understanding of thermal radiation, a phenomenon indispensable across myriad scientific and engineering fields. A profound grasp of how thermal energy is universally emitted by all corporeal bodies, contingent upon their absolute temperature, is not merely academic; it is paramount for designing efficient systems and accurately modeling physical processes. This discourse endeavors to elucidate the intricacies of the Stefan-Boltzmann radiation problem, providing a perspicuous apprehension of radiative heat transfer and its inherent temperature dependence.
We shall navigate the foundational tenets governing the energy emission characteristics of objects, progressing beyond a superficial acquaintance to cultivate a deeper insight into this crucial thermodynamic law. Readers will acquire the analytical tools to operationalize the Stefan-Boltzmann equation in diverse real-world scenarios, from optimizing industrial furnaces to comprehending stellar dynamics. Prepare to master this fundamental aspect of blackbody radiation, thereby augmenting your capacity for innovation and problem-solving in areas where efficient thermal management is key.
Table of Contents
- Understanding the Stefan-Boltzmann Law
- The Foundation of Thermal Radiation
- Example Calculation
- Key Insights
- Comparison of Radiated Power
- Key Components of the Stefan-Boltzmann Law
- Historical Context and Significance
- Solving a Stefan-Boltzmann Radiation Problem
- Step 1: Identify the Knowns
- Step 2: Calculate Surface Area
- Step 3: Apply the Stefan-Boltzmann Law
- Final Result
- Summary of the Example
- Numerical Problems and Solutions
- Numerical Problems and Solutions: Stefan-Boltzmann Law
- Problem 1: Power Radiated by a Black Body
- Problem 2: Temperature from Radiated Power
- Problem 3: Radius of a Radiating Sphere
- Problem 4: Power at Room-like Temperature
- Problem 5: Temperature from Given Power
- Summary of Results
- Key Takeaways
Read More
The pervasive phenomenon of thermal radiation constitutes a seminal mechanism governing energy transfer throughout the cosmos, manifesting from the incandescent photospheres of stellar bodies to the frigid vacuity of interstellar space. This comprehensive blog post embarks upon an exhaustive explication of the Stefan-Boltzmann radiation problem, an indispensable framework for comprehending how all corporeal objects emit thermal energy based on their absolute temperature. A profound grasp of this principle is pivotal across myriad scientific and engineering disciplines, crucial for understanding radiative heat transfer and blackbody radiation.
Within these ensuing sections, we shall meticulously delve into the foundational Stefan-Boltzmann law principles, equipping you with a robust theoretical understanding of energy emission by temperature. Beyond mere conceptualization, we will then proceed to resolve a pertinent practical problem, thereby demonstrating the empirical utility of this essential physical law and its role in thermal management. Finally, we shall consider the far-reaching implications of Stefan-Boltzmann radiation, underscoring its relevance in fields ranging from astrophysics—such as calculating stellar luminosity—to material science and advanced engineering applications.
Understanding the Stefan-Boltzmann Law
The Stefan-Boltzmann Law is a fundamental principle of thermal radiation. It describes how much energy a perfect black body radiates depending solely on its absolute temperature. This law is essential in astrophysics, climate science, and engineering, as it helps quantify energy emission from stars, planets, furnaces, and everyday heated objects.
The Foundation of Thermal Radiation
The law is mathematically expressed as:
### P = \sigma A T^4 ###
- P = total power radiated (Watts, W)
- σ = Stefan-Boltzmann constant ≈ ##5.67 \times 10^{-8} \, \text{W/m}^2\text{K}^4##
- A = surface area of the emitting body (m²)
- T = absolute temperature of the body (Kelvin, K)
The proportionality to the fourth power of temperature means that even a modest increase in temperature leads to a large increase in radiated power. For example, doubling the temperature of a body increases its radiation by 16 times.
Example Calculation
Problem: A black body with a surface area of 2 m² is at 600 K. How much power does it radiate?
Solution:
### P = \sigma A T^4 = (5.67 \times 10^{-8})(2)(600^4) ###
### P = (5.67 \times 10^{-8})(2)(1.296 \times 10^{11}) ###
### P ≈ 1.47 \times 10^4 \,\text{W} = 14.7 \,\text{kW} ###
Answer: The object radiates approximately 14.7 kW of power.
Key Insights
- Temperature sensitivity: Radiated power rises steeply with temperature (∝T⁴).
- Surface area: Larger areas emit more radiation at the same temperature.
- Real objects: Actual bodies emit less than a perfect black body. Their emission is corrected by multiplying with emissivity (ε), giving ### P = \epsilon \sigma A T^4 ### where 0 ≤ ε ≤ 1.
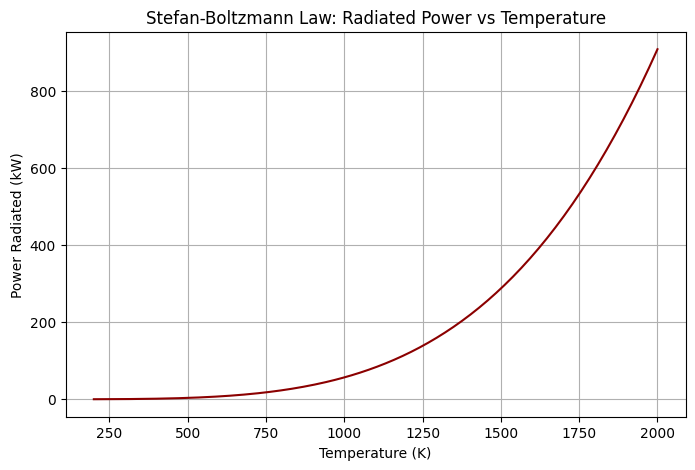
This graph would show the steep exponential-like growth in radiated power with temperature, emphasizing why stars and hot furnaces emit vast amounts of energy compared to everyday objects at room temperature.
Comparison of Radiated Power
| Temperature (K) | Relative Power (P ∝ T⁴) | Remarks |
|---|---|---|
| 300 K (room temperature) | 1 (baseline) | Weak infrared emission |
| 600 K | 16 | Hot surfaces glow faintly red |
| 1200 K | 256 | Bright red glow, intense radiation |
| 6000 K (Sun’s surface) | 1.6 × 10⁶ | Huge power output, visible light dominant |
Key Components of the Stefan-Boltzmann Law
To use the Stefan-Boltzmann Law effectively, it is important to understand its components:
- Stefan-Boltzmann Constant (σ): A universal constant that connects temperature to radiated energy. Its value is approximately ##5.67 \times 10^{-8} \,\text{W/m}^2\text{K}^4##.
- Surface Area (A): Determined by the geometry of the body. For spheres, it is given by ##A = 4\pi r^2##.
- Temperature (T): Must always be in absolute units (Kelvin) when applied to the law.
Historical Context and Significance
The law was first formulated empirically by Josef Stefan in 1879 based on experimental results. Later, in 1884, Ludwig Boltzmann derived it theoretically from thermodynamic and electromagnetic principles. This achievement not only clarified thermal radiation but also connected classical thermodynamics with electromagnetism, paving the way toward the quantum theory of radiation.
The Stefan-Boltzmann Law remains vital in astrophysics (estimating stellar luminosities), climate science (Earth’s radiative balance), and engineering (thermal emission in furnaces and heat exchangers).
Solving a Stefan-Boltzmann Radiation Problem
Step 1: Identify the Knowns
- Radius of sphere: ##r = 0.5\,\text{m}##
- Temperature: ##T = 1000\,\text{K}##
- Stefan-Boltzmann constant: ##\sigma = 5.67 \times 10^{-8}\,\text{W/m}^2\text{K}^4##
Surface area of a sphere is: ### A = 4 \pi r^2 ###
Step 2: Calculate Surface Area
### A = 4 \pi (0.5)^2 = 4 \pi (0.25) = \pi \,\text{m}^2 \approx 3.14\,\text{m}^2 ###
Step 3: Apply the Stefan-Boltzmann Law
### P = \sigma A T^4 = (5.67 \times 10^{-8})(3.14)(1000^4) ###
### P = (5.67 \times 10^{-8})(3.14)(10^{12}) ###
### P \approx 1.78 \times 10^5 \,\text{W} ###
Final Result
The spherical black body radiates approximately 178,000 W (178 kW) of power. This demonstrates the enormous energy output possible at high temperatures, emphasizing the fourth-power dependence on temperature.
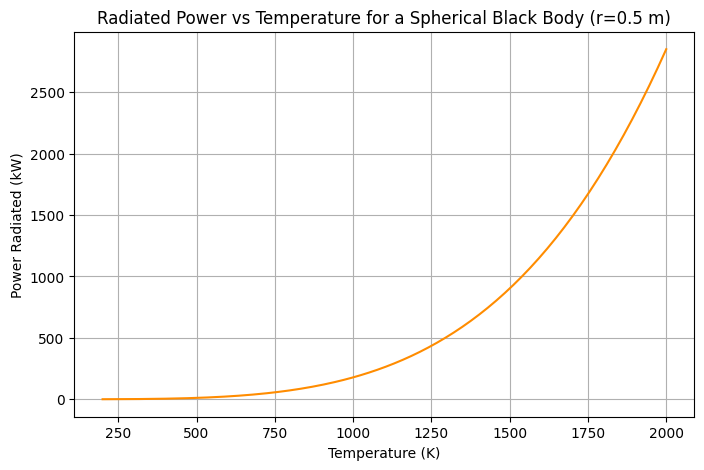
The curve rises steeply, showing that even slight increases in temperature result in dramatically higher radiated power, underscoring the importance of the Stefan-Boltzmann T⁴ relationship.
Summary of the Example
| Quantity | Value |
|---|---|
| Radius (r) | 0.5 m |
| Surface Area (A) | 3.14 m² |
| Temperature (T) | 1000 K |
| Radiated Power (P) | 178 kW |
Numerical Problems and Solutions
To further solidify your understanding, here are some similar problems with brief solutions:
Problem 1
Calculate the power radiated by a black body with an area of 1 m² at a temperature of 500 K.
Problem 2
Determine the temperature of a black body radiating 1000 W with a surface area of 0.1 m².
Problem 3
Find the radius of a spherical black body at 2000 K radiating 500,000 W.
Problem 4
What is the power radiated by a black body at 300 K with an area of 2 m²?
Problem 5
A black body emits 2000 W and has a surface area of 0.5 m². What is its temperature?
Numerical Problems and Solutions: Stefan-Boltzmann Law
Here are a set of worked-out problems that demonstrate how to apply the Stefan-Boltzmann Law (### P = \sigma A T^4 ###) in different scenarios. These examples help reinforce the concepts of temperature, surface area, and power radiation.
Problem 1: Power Radiated by a Black Body
Given: Area A = 1 m², Temperature T = 500 K.
Solution:
### P = \sigma A T^4 = (5.67 \times 10^{-8})(1)(500^4) \approx 3540 \,\text{W} ###
Answer: ≈ 3,540 W.
Problem 2: Temperature from Radiated Power
Given: Power P = 1000 W, Area A = 0.1 m².
Solution:
### T = \left( \dfrac{P}{\sigma A} \right)^{1/4} = \left( \dfrac{1000}{5.67 \times 10^{-8} \cdot 0.1} \right)^{1/4} \approx 996 \,\text{K} ###
Answer: ≈ 996 K.
Problem 3: Radius of a Radiating Sphere
Given: Power P = 500,000 W, Temperature T = 2000 K.
Solution:
Surface area of sphere: ### A = 4 \pi r^2 ### Apply Stefan-Boltzmann Law: ### P = \sigma A T^4 = \sigma (4 \pi r^2) T^4 ###
Rearrange for r: ### r = \sqrt{ \dfrac{P}{4 \pi \sigma T^4} } ###
### r = \sqrt{ \dfrac{500000}{4 \pi (5.67 \times 10^{-8})(2000^4)} } \approx 0.21 \,\text{m} ###
Answer: ≈ 0.21 m.
Problem 4: Power at Room-like Temperature
Given: A = 2 m², T = 300 K.
Solution:
### P = \sigma A T^4 = (5.67 \times 10^{-8})(2)(300^4) \approx 918 \,\text{W} ###
Answer: ≈ 918 W.
Problem 5: Temperature from Given Power
Given: P = 2000 W, A = 0.5 m².
Solution:
### T = \left( \dfrac{P}{\sigma A} \right)^{1/4} = \left( \dfrac{2000}{5.67 \times 10^{-8} \cdot 0.5} \right)^{1/4} \approx 1120 \,\text{K} ###
Answer: ≈ 1120 K.
Summary of Results
| Problem | Knowns | Result |
|---|---|---|
| 1 | A=1 m², T=500 K | P ≈ 3540 W |
| 2 | P=1000 W, A=0.1 m² | T ≈ 996 K |
| 3 | P=500,000 W, T=2000 K | r ≈ 0.21 m |
| 4 | A=2 m², T=300 K | P ≈ 918 W |
| 5 | P=2000 W, A=0.5 m² | T ≈ 1120 K |
Key Takeaways
The Stefan-Boltzmann radiation problem provides a powerful tool for understanding and quantifying thermal radiation. By mastering the law and its applications, you can analyze heat transfer in various scenarios, from astrophysical phenomena to industrial processes. This understanding is crucial for advanced physics and engineering studies.
| Parameter | Value | Unit |
|---|---|---|
| Stefan-Boltzmann Constant (σ) | ##5.67 x 10^{-8}## | W/m²K⁴ |
| Surface Area (A) | ##4πr²## | m² |
| Temperature (T) | Absolute temperature | Kelvin (K) |
| Total Power Radiated (P) | ##P = σAT⁴## | Watts (W) |
We also Published
RESOURCES
- Stefan–Boltzmann law – Wikipedia
- Radiation – Practice – The Physics Hypertextbook
- Stefan Boltzmann Law
- Group Problems #13 – Solutions
- Group Problems #13 – Solutions
- Hawking radiation, the Stefan–Boltzmann law, and unitarization …
- Stefan-Boltzmann Law – GeeksforGeeks
- [University Physics: Stefan-Boltzmann Law and Wien’s Law …
- A Study of the One-Dimensional Heat-Conduction Equation with …
- Solved 1. (Problem 13.4-7) Stefan-Boltzmann Law. Use the | Chegg …





0 Comments