Projectile motion is one of the most elegant applications of classical mechanics. While the basic version considers a projectile launched on a horizontal surface, an important extension is when the projectile is launched on an inclined plane. This scenario not only adds complexity but also reveals the power of resolving motion into suitable axes. In this article, we will explore the mathematics and physics of Projectile Motion on an Inclined Plane, derive general formulas, work out numerical examples, and even simulate the motion using Python.
We will particularly investigate two situations: one where a particle is launched at \(45^\circ\) to the horizontal on a plane inclined at \(30^\circ\), and another where the launch angle is chosen so that the projectile strikes the incline perpendicularly. Together, these cases illustrate both the beauty of theory and the necessity of consistency in applying conditions.
Table of Contents
- Understanding Projectile Motion on an Incline
- Case 1: Launch at \(45^\circ\) on a \(30^\circ\) Incline – Why Perpendicular Impact is Impossible
- Case 2: Correct Launch Angle for Perpendicular Impact
- General Condition for Perpendicular Impact
- Table: Conditions and Results
- Python Simulation of the Trajectory
We Also Published

Understanding Projectile Motion on an Incline
When analyzing projectiles on an inclined plane, the trick is to choose axes that simplify the problem. Instead of the usual horizontal and vertical axes, we align the x-axis along the incline and the y-axis perpendicular to it. This way, the plane itself becomes the reference surface (y = 0). The motion then reduces to familiar equations of motion but in rotated coordinates.
Suppose a projectile is launched with speed \(u\) at angle \(\beta\) to the inclined surface. Let the incline be tilted at angle \(\theta\) to the horizontal. Then:
Velocity components:
\(u_x = u \cos \beta,\qquad u_y = u \sin \beta\)
Acceleration components due to gravity:
\(a_x = -g \sin \theta,\qquad a_y = -g \cos \theta\)
Equations of motion:
\(x(t) = u_x t + \tfrac{1}{2} a_x t^2,\qquad y(t) = u_y t + \tfrac{1}{2} a_y t^2\)
The projectile returns to the incline when \(y=0\). Additional conditions may be imposed depending on whether we want perpendicular or parallel impact.
Case 1: Launch at \(45^\circ\) on a \(30^\circ\) Incline – Why Perpendicular Impact is Impossible
Let us start with the given problem. A particle is projected at \(45^\circ\) to the horizontal with speed \(20\sqrt{2}\,\text{m/s}\) from an incline tilted at \(30^\circ\). The question states that it strikes the plane perpendicularly. Let’s verify this.
The angle with the incline is \(\beta = 45^\circ – 30^\circ = 15^\circ\).
Now, for a perpendicular hit, two conditions must hold simultaneously:
- The projectile is back on the plane: \(y(T)=0\).
- The velocity is purely perpendicular to the plane: \(v_x(T)=0\).
Imposing both conditions leads to the relation \(\tan \beta = \frac{1}{2\tan \theta}\). Substituting \(\theta=30^\circ\) gives \(\beta \approx 40.9^\circ\). But here \(\beta = 15^\circ\). Hence, there is a contradiction. The perpendicular impact is impossible in this setup.
If we only apply \(v_x(T)=0\), we get \(T = 2(\sqrt{3}+1)\,\text{s}\). However, at this time the projectile is not on the incline, so the condition is incomplete. This is why the original question as framed is inconsistent.
Case 2: Correct Launch Angle for Perpendicular Impact
Now let us fix the condition. Suppose the incline angle remains \(\theta = 30^\circ\). For perpendicular impact, the launch angle relative to the incline must be \(\tan \beta = \frac{1}{2\tan \theta}\).
Thus, \(\beta \approx 40.9^\circ\). Relative to the horizontal, this is \(\beta+\theta \approx 70.9^\circ\).
Time of flight is then:
\(T = \frac{2u \sin \beta}{g\cos \theta}\)
Substituting values: \(u=20\sqrt{2}, g=10, \theta=30^\circ, \beta=40.9^\circ\):
\(T \approx 4.28\,\text{s}\).
This satisfies both conditions, proving that the projectile indeed strikes the incline perpendicularly.
General Condition for Perpendicular Impact
The beauty of the result is that it provides a neat relation:
\(\tan \beta = \frac{1}{2\tan \theta}\)
This formula can be applied to any incline angle. It neatly encodes the geometry required for a projectile to meet its incline perpendicularly.
Table: Conditions and Results
| Incline Angle (θ) | Launch Angle w.r.t Horizontal | Launch Angle w.r.t Incline (β) | Time of Flight | Impact Condition |
|---|---|---|---|---|
| 30° | 45° | 15° | 2(√3 + 1) s (not valid) | Not perpendicular |
| 30° | 70.9° | 40.9° | ≈ 4.28 s | Perpendicular |
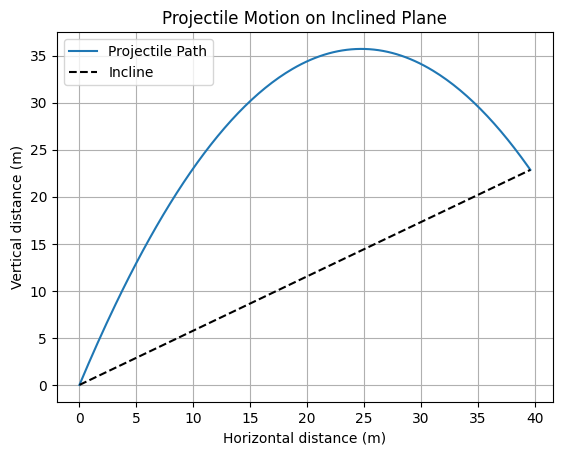
Python Simulation of the Trajectory
We can simulate projectile motion on an incline using Python and visualize the path. Below is a code snippet using matplotlib.
import numpy as np
import matplotlib.pyplot as plt
# Parameters
u = 20*np.sqrt(2) # initial speed
g = 10
theta = np.radians(30) # incline angle
beta = np.radians(40.893) # relative to plane (for perpendicular case)
# Components
ux = u*np.cos(beta)
uy = u*np.sin(beta)
ax = -g*np.sin(theta)
ay = -g*np.cos(theta)
# Time of flight
T = (2*uy)/(-ay)
t = np.linspace(0, T, 200)
x = ux*t + 0.5*ax*t**2
y = uy*t + 0.5*ay*t**2
# Convert to horizontal-vertical coordinates
X = x*np.cos(theta) - y*np.sin(theta)
Y = x*np.sin(theta) + y*np.cos(theta)
# Incline line
X_line = np.linspace(0, max(X), 200)
Y_line = X_line*np.tan(theta)
plt.plot(X, Y, label="Projectile Path")
plt.plot(X_line, Y_line, 'k--', label="Incline")
plt.xlabel("Horizontal distance (m)")
plt.ylabel("Vertical distance (m)")
plt.legend()
plt.title("Projectile Motion on Inclined Plane")
plt.grid(True)
plt.show()This program plots the trajectory of the projectile along with the incline, confirming perpendicular impact visually.
From our network :
- Bitcoin price analysis: Market signals after a muted weekend
- Limit Superior and Inferior
- Optimizing String Concatenation in Shell Scripts: quotes, arrays, and efficiency
- Limits: The Squeeze Theorem Explained
- The Diverse Types of Convergence in Mathematics
- JD Vance Charlie Kirk: Tribute and Political Strategy
- Optimizing String Concatenation in JavaScript: Template Literals, Join, and Performance tips
- Economic Importance of Soybeans in America: The $60 Billion Crop That Feeds the World
- Bitcoin Hits $100K: Crypto News Digest
RESOURCES
- Projectile Motion on an Incline Plane - College Physics - YouTube
- Projectile on Inclined Plane (is this question even real) : r ...
- Physics 3.1: Projectile Motion on an Incline (1 of 7) Example 1 ...
- Projectile Motion Along an Incline | JEE Main | JEE Advanced
- Projectile Motion on an Incline - YouTube
- Projectile Motion on Inclined Plane - Formula, Derivation & Questions
- Projectile Motion on an Inclined Plane.
- Quick Guide to Max Range in Inclined Plane Motion
- Projectile Motion and Inclined Planes - Free Sketchy MCAT Lesson
- Projectile Motion - Kinematics | Air Resistance | Parabolic Curve ...
- Projectile Motion with an Inclined Plane—Super Value Laboratory ...
- An explanation of projectile motion up an inclined plane
- How does projectile motion on an inclined plane work? - Formula ...
- homework and exercises - Projectiles on inclined planes with ...
- calculus - Time of flight for projectile on inclined plane - Mathematics ...






3 Comments