Alright, let’s dive into a fundamental concept in mathematics: the Ordered pair definition. You’ll quickly discover that ordered pairs are the bedrock upon which much of coordinate geometry and related fields are built. They might seem simple at first glance, but understanding the Ordered pair definition is absolutely crucial for anyone venturing into algebra, calculus, or even more advanced mathematical territories. We’ll break down what they are, how they work, and why they’re so incredibly important.

So, what exactly is an ordered pair? In essence, it’s a way to represent a point or a relationship between two values, and the order in which those values appear matters a great deal. The Ordered pair definition dictates that the first value represents the x-coordinate (horizontal position), and the second value represents the y-coordinate (vertical position) on a graph. We’ll explore this further, looking at examples and applications to solidify your understanding. Furthermore, we will see how this concept extends into relations and functions, providing a framework for modeling and analyzing a wide range of mathematical scenarios.

---

---

This post delves into the fundamental concept of ordered pairs in mathematics. Ordered pairs are the building blocks of coordinate geometry and are essential for understanding various mathematical concepts. We will explore their definition, characteristics, applications, and provide illustrative examples to solidify your understanding. The concept of ordered pairs is crucial for anyone studying mathematics, from basic algebra to advanced calculus and beyond. The Ordered Pair Definition is a cornerstone of mathematical notation.

What is an Ordered Pair?

An ordered pair is a pair of mathematical objects, typically numbers, where the order in which they are written is significant. It is usually represented in the form (a, b). Here, a is the first element, and b is the second element. The order matters; hence, (a, b) is not the same as (b, a) unless a and b are equal. This seemingly simple concept forms the basis for representing points in space, defining relations, and understanding functions. The significance of the Ordered Pair Definition cannot be overstated in the context of mathematical representation and analysis. Without ordered pairs, we would lack a fundamental tool for visualizing and analyzing mathematical relationships.

---

An ordered pair, denoted (a, b), is a fundamental mathematical object consisting of two elements where the order matters: “a” is the first element and “b” the second, such that (a, b) ≠ (b, a) unless a = b; formally defined in set theory (e.g., Kuratowski’s {{a}, {a, b}}) to encode order, it underpins relations, functions, and coordinate systems.

---

Ordered Pair Definition and its Significance

The Ordered Pair Definition is the cornerstone of coordinate geometry. It provides a systematic way to locate points in a plane or space. The first element, often denoted as the x-coordinate, represents the horizontal position, while the second element, the y-coordinate, represents the vertical position. For instance, in the ordered pair (3, 4), 3 indicates the position along the x-axis, and 4 indicates the position along the y-axis. This simple notation allows us to graph equations, define functions, and represent vectors. The concept extends to three dimensions with ordered triples (x, y, z) and beyond, making it a versatile tool across various mathematical disciplines. The historical context of ordered pairs is rooted in the development of coordinate geometry by René Descartes, which revolutionized how mathematicians visualized and solved problems.

Illustrative Examples

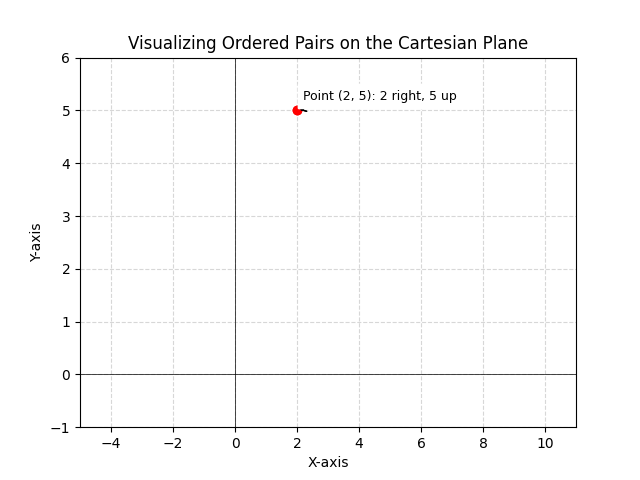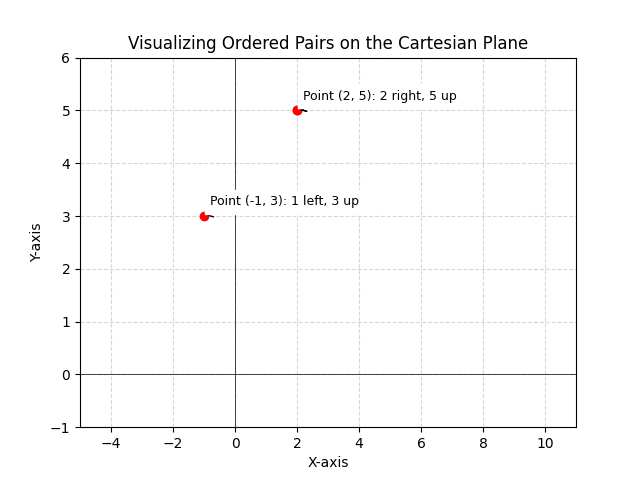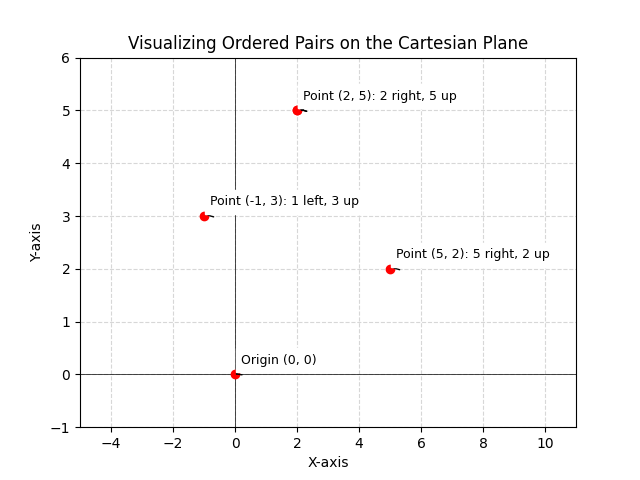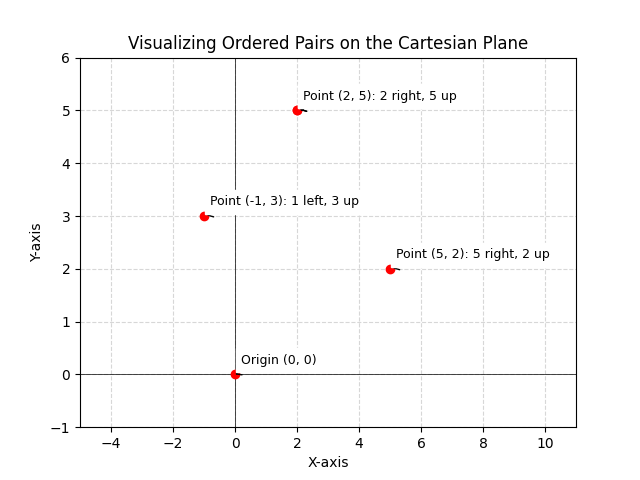
Consider the ordered pair (2, 5). This represents a point on the Cartesian plane. To locate this point, we move 2 units along the x-axis (horizontally) and 5 units along the y-axis (vertically). Similarly, the ordered pair (-1, 3) represents a point located 1 unit to the left of the origin and 3 units up. The difference between (2, 5) and (5, 2) is crucial; they represent entirely different points. (2, 5) is 2 units right and 5 units up, while (5, 2) is 5 units right and 2 units up. This highlights the importance of the order in an ordered pair. Another example is the ordered pair (0, 0), which represents the origin, the point where the x-axis and y-axis intersect. The use of ordered pairs is not limited to simple points; they are also used to represent vectors, which have both magnitude and direction, and to define relations and functions, which map inputs to outputs.

---

---

Characteristics and Applications of Ordered Pairs

The primary characteristic of an ordered pair is that the order of the elements matters. This is in stark contrast to sets, where the order does not affect the set’s identity. For example, the set {1, 2} is the same as the set {2, 1}. However, the ordered pair (1, 2) is different from the ordered pair (2, 1). This fundamental difference is what makes ordered pairs so powerful for representing locations and relationships. They are used extensively in coordinate geometry to plot points, graph equations, and understand geometric shapes. The concept of ordered pairs extends beyond simple plotting; they are used to define relations and functions, which are fundamental concepts in mathematics. The Ordered Pair Definition is crucial for understanding these concepts.

Applications in Coordinate Geometry

In coordinate geometry, ordered pairs are used to locate points on the Cartesian plane. Each ordered pair (x, y) corresponds to a unique point. The x-coordinate represents the horizontal distance from the origin (0, 0), and the y-coordinate represents the vertical distance. For example, the ordered pair (4, -3) represents a point located 4 units to the right of the origin and 3 units down. This system allows us to visualize equations and geometric shapes. The graph of a linear equation, such as y = 2x + 1, is a set of ordered pairs that satisfy the equation. Each ordered pair (x, y) on the line represents a solution to the equation. Similarly, the graph of a circle, a parabola, or any other geometric shape is defined by a set of ordered pairs. The ability to represent geometric concepts using ordered pairs is a cornerstone of modern mathematics and physics, enabling the use of algebraic methods to solve geometric problems.

Applications in Relations and Functions

Ordered pairs are also used to define relations and functions. A relation is a set of ordered pairs, where each ordered pair represents a relationship between two elements. A function is a special type of relation where each input (x-value) corresponds to exactly one output (y-value). For example, the relation {(1, 2), (3, 4), (5, 6)} is a set of ordered pairs that defines a relationship between the numbers. The function f(x) = x + 1 can be represented as a set of ordered pairs, such as {(0, 1), (1, 2), (2, 3)}, where the x-value is the input, and the y-value is the output. The concept of ordered pairs allows us to represent complex mathematical relationships in a clear and concise manner. This is particularly important in calculus, where functions are used to model rates of change and other dynamic processes. The use of ordered pairs in defining functions is a critical aspect of mathematical modeling and analysis.

Additional Problems and Solutions

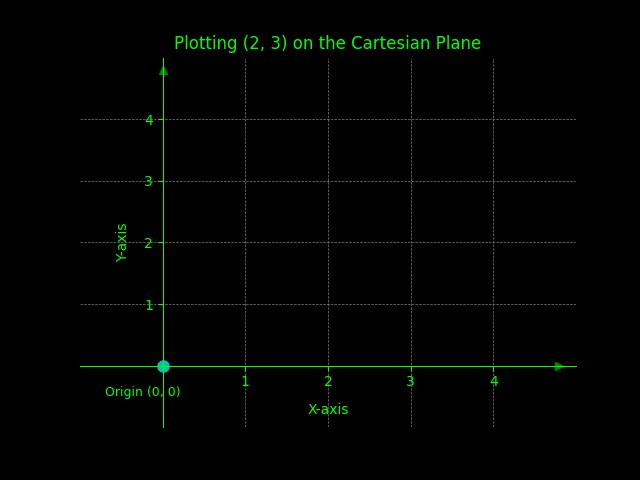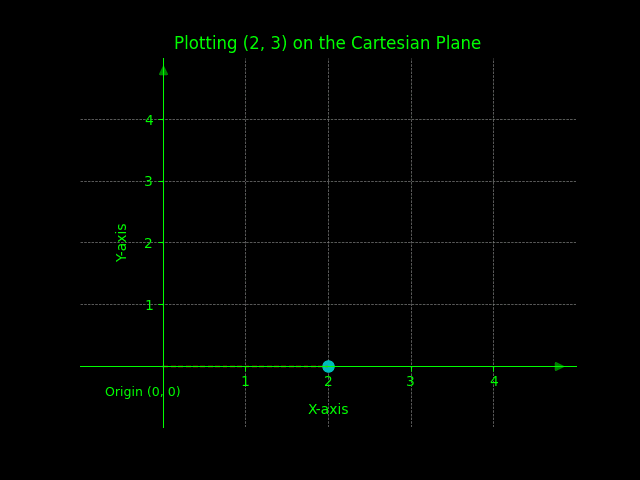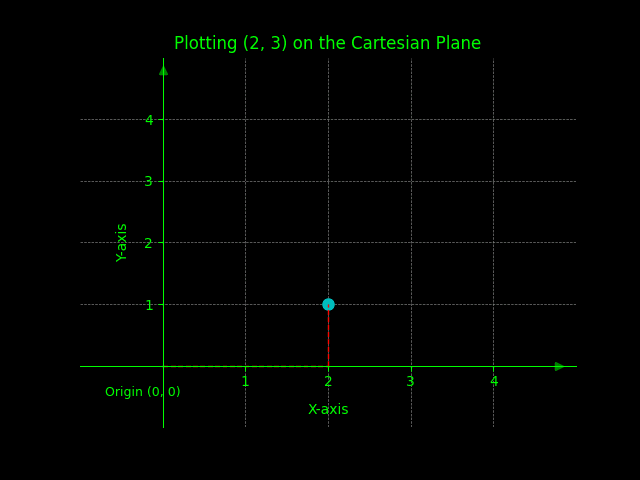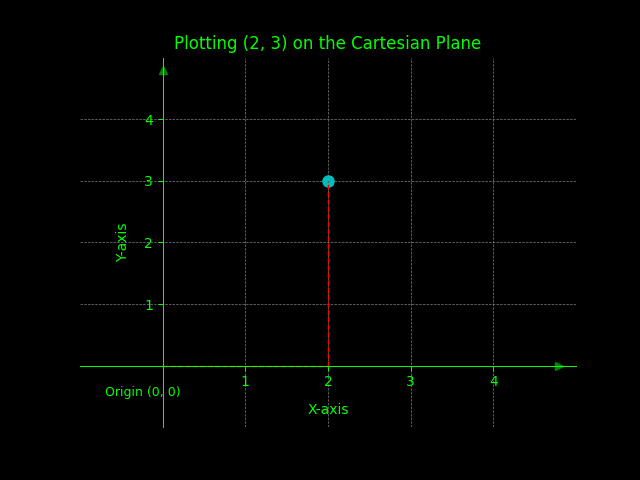
Problem 1: Plot the ordered pair (2, 3) on the Cartesian plane.

Solution: Move 2 units to the right on the x-axis and 3 units up on the y-axis.

Graphic solution shown below.

Problem 2: Determine the quadrant in which the ordered pair (-4, 1) lies.

Solution: Quadrant II (negative x, positive y).

Problem 3: Given the equation y = x – 1, find the ordered pair when x = 5.

Solution: Substitute x = 5 into the equation: y = 5 – 1 = 4. The ordered pair is (5, 4).

Problem 4: What is the distance between the points (1, 2) and (4, 6)?

Solution: Use the distance formula: ##\sqrt{(4-1)^2 + (6-2)^2} = \sqrt{3^2 + 4^2} = \sqrt{25} = 5##.

Problem 5: If a function is defined by f(x) = 2x, what is the ordered pair when x = -2?

Solution: Substitute x = -2 into the function: f(-2) = 2 * -2 = -4. The ordered pair is (-2, -4).

---

---