The concept of linear thermal expansion is vital for anyone studying physics or engineering. You’ll learn about linear thermal expansion and its practical implications in real-world scenarios. This article explores the fundamental principles and provides a clear example.
Understanding linear thermal expansion is critical for designing structures, machinery, and everyday objects that operate reliably across varying temperatures. It helps engineers prevent material damage, ensure precise fits, and predict the behavior of substances when exposed to heat or cold.
Table of Contents
- Understanding Linear Thermal Expansion
- Linear Thermal Expansion
- Meaning of the Coefficient α
- Example Calculation
- Typical Values of Coefficient of Linear Expansion
- Factors Affecting Expansion
- Factors Affecting Expansion
- 1. Original Length (L₀)
- 2. Coefficient of Linear Expansion (α)
- 3. Temperature Change (ΔT)
- Summary Table of Influencing Factors
- Solving a Linear Thermal Expansion Example
- Numerical Problems
- Solved Problems on Linear Thermal Expansion
- Problem 1: Copper Wire
- Problem 2: Railway Track (Steel)
- Problem 3: Brass Rod
- Problem 4: Aluminium Bar
- Problem 5: Steel Cable (Imperial Units)
- Summary of Results
- Key Takeaways
Read More
The phenomenon of linear thermal expansion is crucial in various engineering applications, from designing bridges to understanding the behavior of materials under different temperatures. We will dive into a detailed example, demonstrating how to calculate the change in length of a material due to temperature variations. This knowledge is fundamental for anyone studying physics or engineering, as it underpins many real-world applications.
Understanding Linear Thermal Expansion
Discover the core principles behind how materials respond to temperature changes. The concept of linear thermal expansion example is fundamental in understanding how materials expand or contract. This expansion or contraction is directly proportional to the temperature change.
The Basic Formula
The linear thermal expansion is typically described by the formula: ###ΔL = αL₀ΔT###
where
##ΔL## represents the change in length,
##α## is the coefficient of linear expansion,
##L₀## is the original length,
and ##ΔT## is the change in temperature.
The coefficient of linear expansion ##α## is a material property that indicates how much a material expands or contracts per degree Celsius or Fahrenheit.
Linear Thermal Expansion
When solids are heated or cooled, their dimensions change due to the movement of atoms or molecules. This dimensional change, when considered along one dimension (length), is described by the linear thermal expansion formula:
### \Delta L = \alpha \, L_0 \, \Delta T ###
- ΔL → Change in length (m)
- α → Coefficient of linear expansion (per °C or per K)
- L₀ → Original length of the material (m)
- ΔT → Change in temperature (°C or K)
Meaning of the Coefficient α
The coefficient of linear expansion (##\alpha##) is a property of the material that indicates how much it expands (or contracts) per unit length for each degree change in temperature. For example, metals generally have higher values of ##\alpha##, meaning they expand more noticeably with heat compared to materials like glass or ceramics.
Example Calculation
Problem: A steel rod of length ##L_0 = 2.0 \,\text{m}## is heated from ##20^\circ\text{C}## to ##120^\circ\text{C}##. If the coefficient of linear expansion for steel is ##\alpha = 1.2 \times 10^{-5}\,\text{°C}^{-1}##, find the increase in length.
Solution:
### \Delta L = \alpha \, L_0 \, \Delta T ###
### \Delta L = (1.2 \times 10^{-5})(2.0)(120-20) = (1.2 \times 10^{-5})(2.0)(100) ###
### \Delta L = 2.4 \times 10^{-3}\,\text{m} = 2.4 \,\text{mm} ###
Answer: The rod expands by 2.4 mm.
Typical Values of Coefficient of Linear Expansion
| Material | Coefficient α (per °C ×10⁻⁶) | Remarks |
|---|---|---|
| Aluminium | 23 | Expands more than steel, useful in cookware |
| Steel | 12 | Moderate expansion, common in construction |
| Copper | 17 | Higher expansion, used in electrical wiring |
| Glass | 9 | Low expansion, used in laboratory equipment |
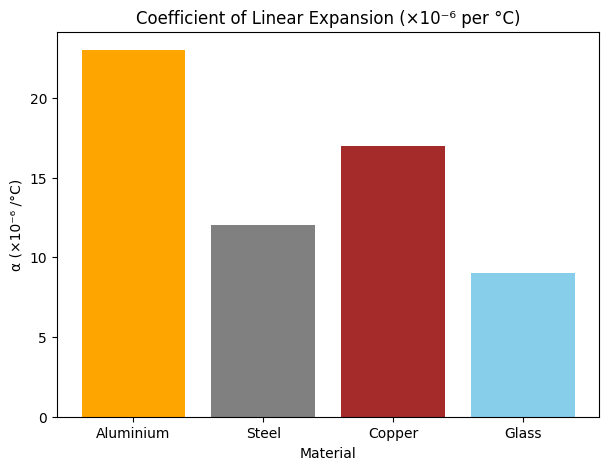
This chart shows how aluminium expands the most per degree rise in temperature, while glass expands the least. Such differences are critical in engineering, construction, and materials science applications.
Factors Affecting Expansion
Several factors influence linear thermal expansion. The original length of the material significantly impacts the overall expansion; longer materials will experience greater length changes for the same temperature variation. Also, different materials have different coefficients of linear expansion, which means they expand and contract at different rates for the same temperature change.
Factors Affecting Expansion
Linear thermal expansion does not occur in isolation; it depends on multiple factors. Understanding these factors is crucial in engineering, construction, and materials science to prevent structural failures, gaps, or stress when temperatures fluctuate. The governing formula is:
### \Delta L = \alpha \, L_0 \, \Delta T ###
From this relation, we can identify three key influences.
1. Original Length (L₀)
The expansion is directly proportional to the original length of the material. A longer rod or beam will undergo a greater absolute change in length than a shorter one for the same material and the same temperature change.
Example: A 2 m steel rod expands twice as much as a 1 m steel rod under identical heating conditions.
2. Coefficient of Linear Expansion (α)
Different materials have unique expansion rates, captured by the coefficient of linear expansion (##\alpha##). Materials with a higher coefficient expand more rapidly when heated. For instance, aluminium expands nearly twice as much as steel for the same rise in temperature.
3. Temperature Change (ΔT)
The greater the change in temperature, the greater the expansion. Heating a material by 100°C produces ten times more expansion than heating it by 10°C, provided other factors remain constant.
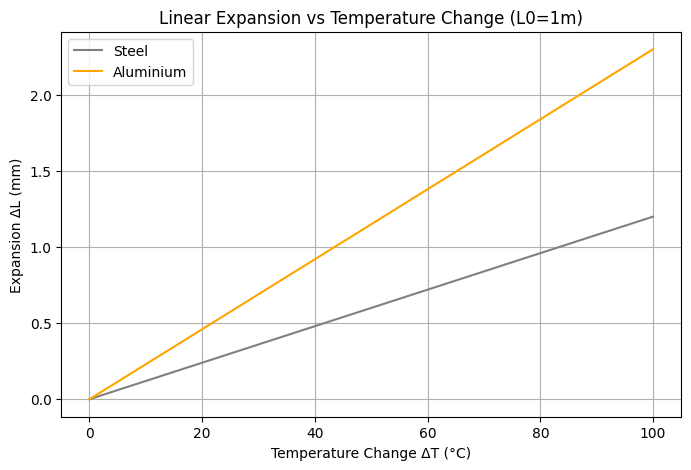
This graph shows aluminium expanding almost twice as much as steel across the same temperature interval, demonstrating how both material properties (α) and temperature change (ΔT) affect expansion.
Summary Table of Influencing Factors
| Factor | Effect on Expansion | Remarks |
|---|---|---|
| Original Length (L₀) | Longer objects expand more | Expansion is proportional to length |
| Coefficient (α) | Higher α → greater expansion | Depends on material properties |
| Temperature Change (ΔT) | Larger ΔT → greater expansion | Linear relation within moderate ranges |
Solving a Linear Thermal Expansion Example
Let’s analyze a practical linear thermal expansion example to solidify our understanding. We will calculate the expansion of a steel bridge segment. This example illustrates the importance of considering thermal expansion in engineering designs to ensure structural integrity.
Problem Setup
Imagine a 100-meter steel bridge segment. The temperature changes from -5°C to 35°C. The coefficient of linear expansion for steel (##α_\text{steel}##) is approximately ##11 \times 10^-6 /°C##. We need to calculate the change in length of the bridge segment due to this temperature change. Understanding the parameters is critical for accurate calculations.
Step-by-Step Solution
Using the formula ##ΔL = αL₀ΔT##, we can solve this.
The original length ##L₀## is 100 meters.
The change in temperature ##ΔT## is 40°C (35°C – (-5°C)).
Therefore, the calculation is as follows: ##ΔL = (11 x 10^-6 /°C) 100 m 40°C##.
This step-by-step approach is crucial.
Final Calculation and Result
Performing the calculation, we get ###ΔL = 0.044 m###
This means the bridge segment expands by 0.044 meters, or 4.4 centimeters. This expansion, while seemingly small, must be accounted for in bridge design to prevent stress and potential failure. The final result highlights the practical implications.
Numerical Problems
- Problem 1: A copper wire is 50 meters long at 20°C. Calculate its length at 50°C. (##α_\text{copper} = 17 x 10^-6 /°C##).
- Problem 2: A railway track is 1 km long. If the temperature increases by 30°C, how much does it expand? (##α_\text{steel} = 11 x 10^-6 /°C##).
- Problem 3: A brass rod is 2 meters long at 25°C. What is its length at 75°C? (##α_\text{brass} = 19 x 10^-6 /°C##).
- Problem 4: Calculate the expansion of an aluminum bar, 1.5 meters long, with a temperature change of 20°C. (##α_\text{aluminum} = 23 x 10^-6 /°C##).
- Problem 5: A steel cable is 1000 feet long. Find the change in length when the temperature drops by 10°F.
Solved Problems on Linear Thermal Expansion
We use the fundamental relation of linear expansion:
### \Delta L = \alpha \, L_0 \, \Delta T ###
and the new length is:
### L = L_0 + \Delta L ###
Problem 1: Copper Wire
Given: Length ##L_0 = 50\,\text{m}##, initial temperature 20°C, final temperature 50°C, so ##\Delta T = 30^\circ\text{C}##. Coefficient ##\alpha_{\text{Cu}} = 17 \times 10^{-6}/^\circ\text{C}##.
Calculation:
### \Delta L = (17 \times 10^{-6})(50)(30) = 0.0255 \,\text{m} = 2.55\,\text{cm} ###
### L = 50 + 0.0255 = 50.0255\,\text{m} ###
Answer: The wire length becomes 50.0255 m.
Problem 2: Railway Track (Steel)
Given: ##L_0 = 1000\,\text{m}##, ##\Delta T = 30^\circ\text{C}##, ##\alpha_{\text{steel}} = 11 \times 10^{-6}/^\circ\text{C}##.
Calculation:
### \Delta L = (11 \times 10^{-6})(1000)(30) = 0.33\,\text{m} ###
Answer: The track expands by 0.33 m (33 cm).
Problem 3: Brass Rod
Given: ##L_0 = 2.0\,\text{m}##, from 25°C to 75°C (##\Delta T = 50^\circ\text{C}##), ##\alpha_{\text{brass}} = 19 \times 10^{-6}/^\circ\text{C}##.
Calculation:
### \Delta L = (19 \times 10^{-6})(2.0)(50) = 0.0019\,\text{m} = 1.9\,\text{mm} ###
### L = 2.000 + 0.0019 = 2.0019\,\text{m} ###
Answer: Final length is 2.0019 m.
Problem 4: Aluminium Bar
Given: ##L_0 = 1.5\,\text{m}##, ##\Delta T = 20^\circ\text{C}##, ##\alpha_{\text{Al}} = 23 \times 10^{-6}/^\circ\text{C}##.
Calculation:
### \Delta L = (23 \times 10^{-6})(1.5)(20) = 0.00069\,\text{m} = 0.69\,\text{mm} ###
Answer: The bar expands by 0.69 mm.
Problem 5: Steel Cable (Imperial Units)
Given: Length ##L_0 = 1000\,\text{ft}##, temperature drop of 10°F, material = steel.
First convert to SI units: 1000 ft = 304.8 m. For steel, ##\alpha = 11 \times 10^{-6}/^\circ\text{C}##.
Now, convert temperature: 10°F change corresponds to:
### \Delta T = \frac{5}{9} \times 10 = 5.56^\circ\text{C} ###
Calculation:
### \Delta L = (11 \times 10^{-6})(304.8)(-5.56) = -0.0186\,\text{m} ###
= -18.6 mm (negative because length decreases).
Answer: The steel cable shortens by about 18.6 mm (0.0186 m).
Summary of Results
| Problem | Material | Initial Length | ΔT | Expansion (ΔL) | Final Length |
|---|---|---|---|---|---|
| 1 | Copper | 50 m | +30°C | 0.0255 m | 50.0255 m |
| 2 | Steel | 1000 m | +30°C | 0.33 m | 1000.33 m |
| 3 | Brass | 2.0 m | +50°C | 0.0019 m | 2.0019 m |
| 4 | Aluminium | 1.5 m | +20°C | 0.00069 m | 1.50069 m |
| 5 | Steel (imperial) | 1000 ft (304.8 m) | -10°F (≈ -5.56°C) | -0.0186 m | 304.7814 m |
Key Takeaways
The understanding and application of linear thermal expansion example is essential in engineering. This concept ensures the longevity and safety of structures and systems. Always consider temperature variations during the design phase.
| Parameter | Value | Unit |
|---|---|---|
| Original Length (###L₀###) | 100 | meters |
| Initial Temperature | -5 | °C |
| Final Temperature | 35 | °C |
| Change in Temperature (###ΔT###) | 40 | °C |
| Coefficient of Linear Expansion (###α_steel###) | 11 x 10^-6 | /°C |
| Change in Length (###ΔL###) | 0.044 | meters |
We also Published
RESOURCES
- Linear Thermal Expansion: Formula, Coefficients & Calculator
- 1.3 Thermal Expansion – University Physics Volume 2 | OpenStax
- Thermal expansion – Wikipedia
- Thermal Expansion of Solids and Liquids | Physics
- How to Calculate Linear Thermal Expansion for Measurement …
- Coefficient of Thermal Expansion and How to Measure it
- Linear Thermal Expansion Practice Problems | Test Your Skills with …
- 12.3: Thermal Expansion – Physics LibreTexts
- 1.3 Thermal Expansion – General Physics Using Calculus I
- Thermal Expansion





0 Comments