The Squeeze Theorem is a powerful tool in calculus for evaluating limits. It provides a clever method for finding the limit of a function by bounding it between two other functions whose limits are known. This technique is especially useful when dealing with functions that are difficult to analyze directly, offering a straightforward alternative.
Table of Contents
- The Squeeze Theorem
- Applying the Squeeze Theorem
- Limit of ##x^2 \sin(1/x)## as ##x \to 0##
- ###\lim_{x \to 0} x^2 \sin!\left(\tfrac{1}{x}\right).###
- Step-by-Step Solution
- ###-1 \leq \sin!\left(\tfrac{1}{x}\right) \leq 1###
- ###-x^2 \leq x^2 \sin!\left(\tfrac{1}{x}\right) \leq x^2###
- ###\lim_{x \to 0} x^2 \sin!\left(\tfrac{1}{x}\right) = 0###
- Graphical Illustration
- Key Takeaway
- Advanced Applications and Extensions
- Key Takeaways
Read More
The Squeeze Theorem, a cornerstone of calculus, elegantly determines limits by bounding a function between two others. Understanding this theorem is crucial for anyone delving into the intricacies of limits and continuity. It provides a powerful method to evaluate limits that might otherwise be difficult to compute directly. Let’s unravel the core concepts and applications of this vital theorem.
The Squeeze Theorem
The Squeeze Theorem, also known as the Sandwich Theorem or the Pinching Theorem, offers a unique approach to evaluating limits. This approach is particularly effective when dealing with functions that are difficult to analyze directly. The theorem hinges on the idea of bounding a function between two other functions whose limits are known.
Formal Statement of the Theorem
Formally, the Squeeze Theorem states:
If ##g(x) ≤ f(x) ≤ h(x)## for all x in an interval I containing c (except possibly at c itself),
and if ##lim_{x → c} g(x) = L## and ##lim_{x → c} h(x) = L##,
then ##lim_{x → c} f(x) = L##.
This means that if a function f(x) is “squeezed” between two functions, g(x) and h(x), and both g(x) and h(x) approach the same limit L as x approaches c, then f(x) must also approach L.
Visualizing the Concept
Imagine a scenario where you have a function, f(x), whose behavior near a point c is uncertain. However, you can find two other functions, g(x) and h(x), that bound f(x) from below and above, respectively. If g(x) and h(x) converge to the same value as x approaches c, the Squeeze Theorem ensures that f(x) must converge to that same value, as it is “squeezed” between them.
Historical Context and Origins
The origins of the Squeeze Theorem can be traced back to ancient mathematicians like Archimedes and Eudoxus, who used similar geometric techniques to approximate the value of pi. These early methods laid the groundwork for the formalization of the theorem in modern calculus. Carl Friedrich Gauss later contributed to its modern formulation, making it a fundamental tool in limit calculations.
Applying the Squeeze Theorem
Understanding how to apply the Squeeze Theorem is key to mastering its utility. The process involves identifying bounding functions and evaluating their limits. This section provides step-by-step guidance and illustrative examples.
Step-by-Step Application
First, identify the function, f(x), whose limit you want to find. Next, find two functions, g(x) and h(x), such that ##g(x) ≤ f(x) ≤ h(x)##. Then, calculate the limits of g(x) and h(x) as x approaches the target value. If both limits exist and are equal, then by the Squeeze Theorem, the limit of f(x) is the same.
Limit of ##x^2 \sin(1/x)## as ##x \to 0##
We want to evaluate:
###\lim_{x \to 0} x^2 \sin!\left(\tfrac{1}{x}\right).###
Step-by-Step Solution
The function ##\sin(1/x)## oscillates infinitely between ##-1## and ##1## as ##x## approaches 0. However, it is always bounded:
###-1 \leq \sin!\left(\tfrac{1}{x}\right) \leq 1###
Multiplying the inequality by ##x^2## (which is always nonnegative), we get:
###-x^2 \leq x^2 \sin!\left(\tfrac{1}{x}\right) \leq x^2###
Now, take limits of the bounding functions as ##x \to 0##:
- ##\lim_{x \to 0} -x^2 = 0##
- ##\lim_{x \to 0} x^2 = 0##
By the Squeeze Theorem, since both bounds converge to 0, the original limit is also 0:
###\lim_{x \to 0} x^2 \sin!\left(\tfrac{1}{x}\right) = 0###
Graphical Illustration
The following plot shows the graph of ##f(x) = x^2 \sin(1/x)## near 0. The oscillations get smaller and smaller as they are “squeezed” towards 0 by the parabolas ##y = x^2## and ##y = -x^2##.
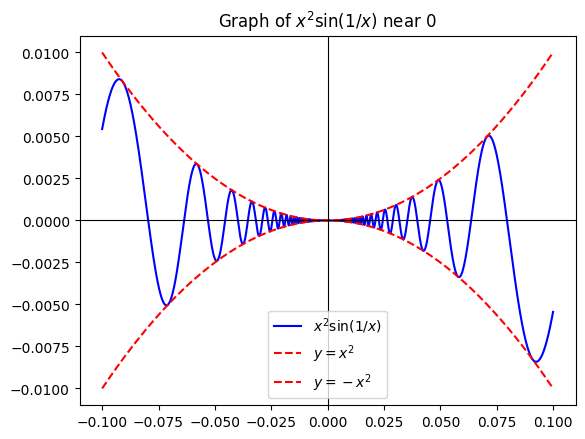
Key Takeaway
Even though ##\sin(1/x)## oscillates infinitely fast as ##x \to 0##, the factor ##x^2## suppresses the oscillations, forcing the whole product towards 0. This is a classic example where the Squeeze Theorem helps to evaluate limits involving oscillating functions.
Example 2: Trigonometric Limit
Another classic example is proving ##lim_{x → 0} (sin(x)/x) = 1##. Using geometric arguments and the unit circle, we can show that for small x, ##cos(x) ≤ sin(x)/x ≤ 1##. Taking the limit as x approaches 0, we find that ##lim_{x → 0} cos(x) = 1##. Hence, by the Squeeze Theorem, ##lim_{x → 0} (sin(x)/x) = 1##.
Practical Implications
The Squeeze Theorem is not just a theoretical concept; it has practical applications in various fields. It helps in determining the behavior of complex functions, particularly those involving trigonometric functions or oscillating behavior. It’s used in physics, engineering, and economics to model and analyze systems.
Advanced Applications and Extensions
Beyond basic applications, the Squeeze Theorem extends to more complex scenarios, including multivariable calculus and sequences. This section explores these advanced aspects, enhancing your understanding of its versatility.
Multivariable Calculus
In multivariable calculus, the Squeeze Theorem can be extended. However, the bounding functions must satisfy the inequality around the point of interest, not just along a path. This means that the inequalities must hold in a two-dimensional or three-dimensional neighborhood around the point, which adds complexity compared to single-variable calculus.
Sequences and Series
The Squeeze Theorem also applies to sequences. If we have three sequences, ##{a_n}##, ##{b_n}##, and ##{c_n}##, such that ##a_n ≤ b_n ≤ c_n## for all n greater than some N, and if ##lim_{n → ∞} a_n = L## and ##lim_{n → ∞} c_n = L##, then ##lim_{n → ∞} b_n = L##. This is a powerful tool for determining the convergence of sequences.
Infinite Intervals
The theorem is also valid for infinite intervals. For instance, if we consider the interval (0, ∞) and have ##g(x) ≤ f(x) ≤ h(x)## for all x in this interval, and if ##lim_{x → ∞} g(x) = L## and ##lim_{x → ∞} h(x) = L##, then ##lim_{x → ∞} f(x) = L##. This extension allows us to analyze the behavior of functions as x approaches infinity.
Key Takeaways
The Squeeze Theorem is a fundamental tool in calculus, providing a robust method for determining limits. By bounding a function between two others, it simplifies the process of evaluating limits, especially when direct methods are challenging. Its applications span various areas of mathematics and science, making it an indispensable concept for anyone studying calculus.
Summary of Benefits
The key benefits of the Squeeze Theorem include its ability to handle complex functions, its applicability to multivariable calculus and sequences, and its use in proving fundamental limit results. It’s a versatile tool that enhances your problem-solving skills and deepens your understanding of calculus.
Final Thoughts
Mastering the Squeeze Theorem is a significant step toward understanding the core concepts of calculus. Its versatility and wide-ranging applications make it an essential concept for students and professionals alike. Continue practicing with different examples to solidify your understanding and become proficient in this essential theorem.
| Concept | Description | Example |
|---|---|---|
| Squeeze Theorem | If ##g(x) ≤ f(x) ≤ h(x)## and ##lim g(x) = lim h(x) = L##, then ##lim f(x) = L##. The Squeeze Theorem is used to determine the limit of a function by using two other functions whose limits are known. | ##lim_{x → 0} x^2 * sin(1/x) = 0##, because ##-x^2 ≤ x^2 * sin(1/x) ≤ x^2## and ##lim_{x → 0} -x^2 = lim_{x → 0} x^2 = 0##. |
| Bounding Functions | Functions ##g(x)## and ##h(x)## that satisfy ##g(x) ≤ f(x) ≤ h(x)##. These functions “squeeze” the function ##f(x)##. | In the example above, ##-x^2## and ##x^2## are the bounding functions. |
| Applications | Used to evaluate limits of trigonometric functions, functions with oscillations, and in multivariable calculus. | Proving ##lim_{x → 0} (sin(x)/x) = 1##. |
We also Published
RESOURCES
- Squeeze theorem – Wikipedia
- Squeeze Theorem – YouTube
- Can someone help explain the squeeze theorem? : r/calculus
- Squeeze Theorem (How-To w/ 4 Step-by-Step Examples!)
- When to use the L’Hopital’s Rule or Squeeze Theorem. The question …
- Squeeze theorem (practice) | Khan Academy
- calculus – Squeeze Theorem for Factorials – Mathematics Stack …
- The Squeeze Theorem
- calculus – Squeeze Theorem on non trig functions – Mathematics …
- Skipping a calculus topic (squeeze theorem) – Mathematics …





0 Comments