Limit superior and limit inferior are essential concepts in mathematical analysis, providing a robust framework to describe the eventual behavior of sequences and functions. They offer a way to quantify the “largest” and “smallest” values a sequence approaches, especially when a standard limit fails to exist. This article will explore the definitions, properties, and applications of these powerful tools.
Table of Contents
Read More
Limit Superior and Limit Inferior
In mathematical analysis, the concepts of limit superior and limit inferior are crucial when studying the behavior of sequences and functions, especially in cases where an ordinary limit does not exist. They provide a way to capture the extreme bounds of a sequence, offering insights into oscillatory and divergent behaviors.
Formal Definitions and Notations
- Limit Superior (denoted ##\limsup_{n \to \infty} x_n## or ##\varlimsup_{n \to \infty} x_n##): The greatest limit point (largest subsequential limit) of the sequence. Formally, ### \limsup_{n \to \infty} x_n = \inf_{n} \left( \sup_{m \geq n} x_m \right). ###
- Limit Inferior (denoted ##\liminf_{n \to \infty} x_n## or ##\varliminf_{n \to \infty} x_n##): The least limit point (smallest subsequential limit). Formally, ### \liminf_{n \to \infty} x_n = \sup_{n} \left( \inf_{m \geq n} x_m \right). ###
Thus, the limit superior gives the “eventual upper bound” of a sequence, while the limit inferior gives the “eventual lower bound.”
Intuitive Understanding
If a sequence oscillates, the limsup identifies the highest accumulation point, and the liminf identifies the lowest. For example, for the oscillating sequence ##x_n = (-1)^n##:
- ##\limsup x_n = 1##
- ##\liminf x_n = -1##
Even though the sequence does not converge, these definitions allow us to capture its long-term oscillatory bounds.
Mathematical Properties
- They always exist in the extended real line (possibly ##\pm \infty##).
- Inequality: ### \liminf_{n \to \infty} x_n \leq \limsup_{n \to \infty} x_n. ###
- If ##\limsup = \liminf##, the sequence converges to that common value.
Applications
- Convergence Analysis: Establishing convergence by comparing limsup and liminf.
- Real Analysis: Used in defining oscillation of functions, continuity analysis, and function bounds.
- Measure Theory: Applied in studying measurable functions and convergence of sets.
- Probability Theory: Essential in results like the Borel-Cantelli Lemma and laws of large numbers.
Illustrative Examples
Example 1: Oscillating Sequence
For ##x_n = (-1)^n##:
- ##\limsup x_n = 1##
- ##\liminf x_n = -1##
Example 2: Convergent Sequence
For ##x_n = \tfrac{1}{n}##:
- ##\limsup x_n = 0##
- ##\liminf x_n = 0##
The sequence converges to 0.
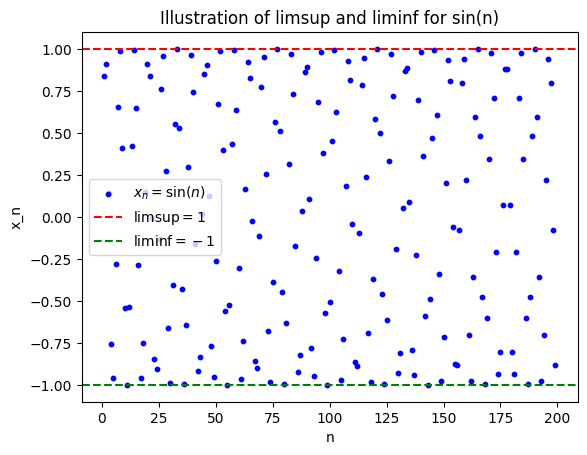
Example 3: Non-Convergent but Bounded Sequence
For ##x_n = \sin(n)##:
- ##\limsup x_n = 1##
- ##\liminf x_n = -1##
The sequence oscillates between -1 and 1.
Summary Table
| Concept | Definition | Significance |
|---|---|---|
| Limit Superior (##\limsup##) | ##\inf_n (\sup_{m \geq n} x_m)## | Captures the eventual upper bound of the sequence. |
| Limit Inferior (##\liminf##) | ##\sup_n (\inf_{m \geq n} x_m)## | Captures the eventual lower bound of the sequence. |
| Convergence | Occurs if ##\limsup = \liminf## | Gives a precise convergence criterion. |
Key Takeaways
- Limit superior and inferior always exist in the extended real numbers.
- They capture oscillatory and divergent behavior of sequences.
- They are fundamental tools in real analysis, measure theory, and probability theory.
- Convergence of a sequence is guaranteed when ##\limsup = \liminf##.
We also Published
RESOURCES
- Limit inferior and limit superior – Wikipedia
- definition – What is limit superior and limit inferior? – Mathematics …
- 2.5: Limit Superior and Limit Inferior – Mathematics LibreTexts
- real analysis – Limit Supremum and Infimum. Struggling the concept …
- RA Limit superior, limit inferior, and Bolzano–Weierstrass
- The Limit Superior and Limit Inferior A number a is called a limit …
- The Limit Inferior and Limit Superior of a Sequence
- STATISTICAL LIMIT SUPERIOR AND LIMIT INFERIOR 1 …
- Can the limit laws for sequences also apply for limit superior and …
- inferior limit in nLab







0 Comments