IIT JEE inductors form a critical part of the physics curriculum, demanding precise numerical skills. This introduction sets the stage for exploring energy storage concepts through practical problems, essential for exam readiness and deeper electromagnetic understanding.
Table of Contents
Read More
Mastering inductor energy calculations is crucial for acing the IIT JEE physics section, as it tests both conceptual understanding and numerical proficiency. This post provides a comprehensive guide to solving problems related to energy stored in inductors, with detailed examples and step-by-step explanations to enhance your preparation.
Fundamentals of Inductor Energy Storage
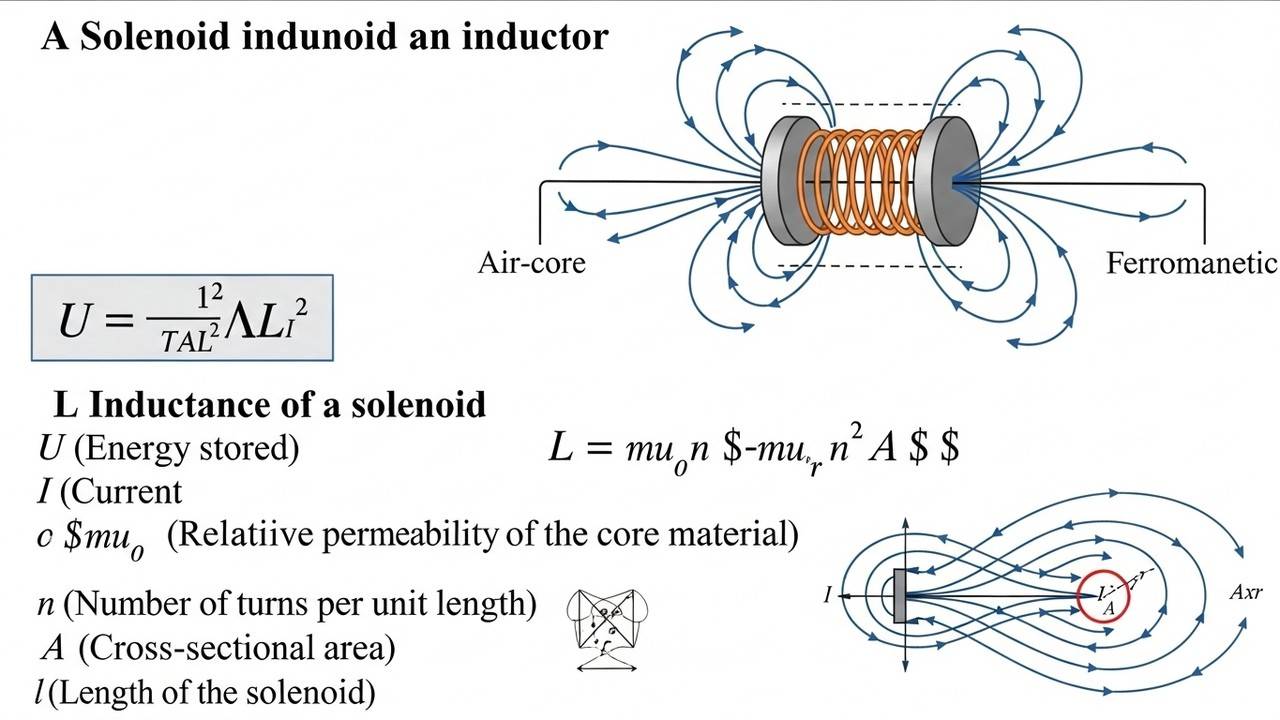
Inductors store energy in their magnetic fields when current flows through them, a principle vital for electromagnetic applications. The energy stored is given by the formula ##U = rac{1}{2} L I^2##, where L is inductance in henries and I is current in amperes.
Understanding the Energy Formula
The formula ##U = rac{1}{2} L I^2## derives from integrating the power over time, reflecting how energy accumulates in the magnetic field. It’s analogous to kinetic energy in mechanics, emphasizing the quadratic dependence on current.
For instance, doubling the current quadruples the stored energy, highlighting the sensitivity to changes in electrical parameters and its implications in circuit design.
Units and Dimensions
Energy is measured in joules, inductance in henries, and current in amperes, ensuring dimensional consistency in calculations. This standardization aids in avoiding errors during problem-solving in exams like IIT JEE.
Remember, 1 henry times ampere squared equals 1 joule, a key conversion that simplifies many numerical problems and reinforces unit analysis skills.
Practical Numerical Applications
Applying these concepts to real-world scenarios sharpens problem-solving abilities, essential for competitive exams. Let’s delve into specific examples that illustrate common pitfalls and strategies.
Example Calculation with Given Values
Given an inductor with L = 2 H and I = 3 A, the energy stored is calculated as ##U = rac{1}{2} \times 2 \times 3^2 = 9## joules. This straightforward computation tests basic formula application.
Variations might involve changing units or adding complexities like time-dependent currents, preparing you for more advanced questions in the IIT JEE syllabus.
Common Mistakes and How to Avoid Them
Students often forget the half in the formula or misapply units, leading to incorrect answers. Always double-check substitutions and ensure consistency in SI units to avoid such errors.
Practice with diverse problems, such as those involving multiple inductors or energy dissipation, to build confidence and accuracy in solving inductor-related numericals.
Key Takeaways
Mastering energy storage in inductors is fundamental for IIT JEE success. Focus on understanding the derivation, practicing varied problems, and avoiding common errors to excel in this topic and boost your overall physics score.
| Parameter | Value | Description |
|---|---|---|
| Inductance (L) | 2 H | Given inductance in henries |
| Current (I) | 3 A | Given current in amperes |
| Energy Stored (U) | 9 J | Calculated using ##U = \frac{1}{2} L I^2## |
| Formula | ##U = \frac{1}{2} L I^2## | Standard formula for energy in inductor |
We also Published
RESOURCES
- capacitor and inductor
- The inductors of the two LR circuits are placed next to each other , a
- Finding Self Induction and Inductors in Series and Parallel | IIT JEE …
- IIT JEE – INDUCTANCE EDUCARE
- Understanding the Differences Between Capacitors and Inductors …
- Consider following two circuits of ideal inductors and resistors. Both …
- IIT-JEE 2010 Paper 2 Offline | Alternating Current Question 13 …
- Electromagnetic Induction – Revision Notes for IIT JEE (Main and …
- [Solved] A series AC circuit containing an inductor (20 mH), a capaci
- Self Inductance of a Solenoid: Formula, Derivation & Uses







0 Comments