The world of electrical circuits often revolves around the concept of capacitance, a fundamental property that dictates how much charge a device can store. IIT JEE capacitance problems are a critical aspect of the IIT JEE examination, testing your understanding of capacitors and their behavior in circuits. This article aims to equip you with the knowledge and skills needed to excel in this area.
Table of Contents
Read More
Welcome, future engineers! In this article, we will dive into the world of capacitors, specifically focusing on IIT JEE capacitance numerical problems. We will explore various aspects, from basic capacitor configurations to more complex combinations, equipping you with the knowledge and skills to tackle challenging problems. Let’s begin our journey into the realm of electrostatics!
Understanding the Fundamentals of Capacitance
The concept of capacitance is fundamental to understanding how electrical energy is stored in a circuit. It is the ability of a capacitor to store charge for a given voltage. We’ll delve into the core principles, ensuring a solid foundation for tackling more complex problems involving IIT JEE capacitance.
Definition and Basic Formula
Capacitance (##C##) is defined as the ratio of the charge (##Q##) stored on a capacitor to the voltage (##V##) across it:
###C = \dfrac{Q}{V}###
This relationship is fundamental for understanding capacitor behavior. The unit of capacitance is the Farad (F). Because 1 F is very large, practical capacitors are often measured in microfarads (µF) or picofarads (pF).
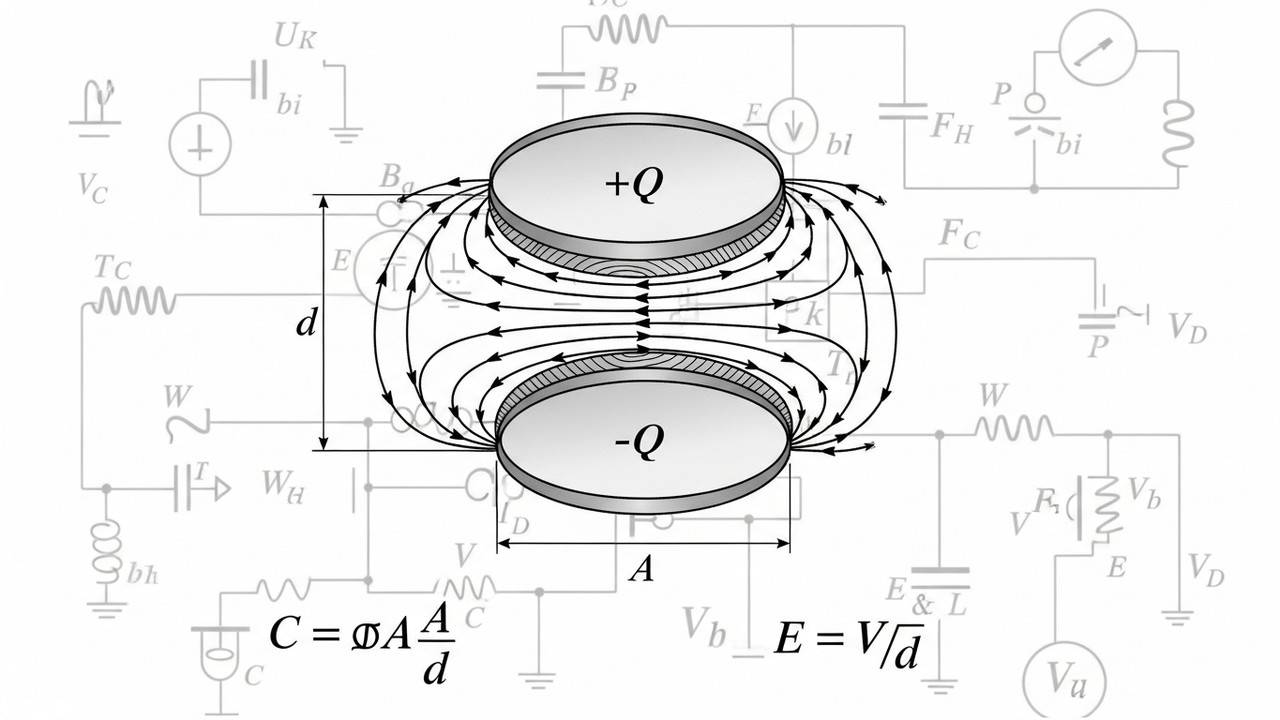
A common example is the parallel-plate capacitor, which consists of two conductive plates separated by a dielectric. Its capacitance depends on plate geometry and separation:
###C = \dfrac{\varepsilon_0 \cdot A}{d}###
where:
##\varepsilon_0 \approx 8.85 \times 10^{-12}\, F/m## is the permittivity of free space,
##A## is the plate area,
##d## is the separation between plates.
Thus, capacitance is directly proportional to the plate area and inversely proportional to the distance between the plates. This principle is central to analyzing capacitors in circuits and is a key concept for **IIT JEE preparation**.
Factors Affecting Capacitance
Several factors influence the capacitance of a capacitor. The key parameters are:
- Plate area (A): Larger plate area increases capacitance since more charge can be stored.
- Distance between plates (d): Greater separation decreases capacitance, as the electric field weakens.
- Dielectric material: The insulating material between plates affects how much charge can be stored for a given voltage.
When a dielectric is introduced, the capacitance increases by a factor called the dielectric constant (##\kappa##). The formula becomes:
###C = \kappa \, \varepsilon_0 \, \dfrac{A}{d}###
where:
##\varepsilon_0 \approx 8.85 \times 10^{-12} \, F/m## is the permittivity of free space,
##\kappa## is the dielectric constant of the material.
Examples of dielectric materials include air, paper, ceramic, and mica. Each has a different dielectric constant, determining how effectively it increases capacitance. The dielectric constant essentially measures how well a material can store electrical energy in an electric field.
By mastering these factors, you gain the ability to analyze, design, and troubleshoot capacitor-based circuits effectively. This knowledge is especially crucial for success in the IIT JEE capacitance section.
Solving Capacitance Numericals: A Step-by-Step Guide
Numerical problems are the ultimate test of your understanding of capacitance. We will work through examples, demonstrating how to apply formulas and concepts to solve real-world problems. This section will help you refine your problem-solving skills and boost your confidence for the IIT JEE capacitance examination.
Problem 1: Parallel Plate Capacitor
A parallel-plate capacitor has plate area ##A = 1\,\text{m}^2##, separation ##d = 0.01\,\text{m}##, and permittivity of free space ##\varepsilon_0 = 8.85 \times 10^{-12}\,\text{F/m}##.
Formula:
###C = \dfrac{\varepsilon_0 \, A}{d}###
Substitute values:
###C = \dfrac{(8.85 \times 10^{-12}\,\text{F/m}) \cdot (1\,\text{m}^2)}{0.01\,\text{m}}###
Compute:
###C = 8.85 \times 10^{-10}\,\text{F} = 0.885\,\text{nF}###
Always keep units consistent (##\text{F/m} \cdot \text{m}^2 / \text{m} = \text{F}##) and double-check powers of ten.
Problem 2: Series and Parallel Combinations
We are asked to calculate the equivalent capacitance of two capacitors, C1 = 2 µF and C2 = 4 µF, first in series and then in parallel.
Series Combination
For capacitors in series, the reciprocal of the equivalent capacitance is the sum of reciprocals:
###\dfrac{1}{C_{eq}} = \dfrac{1}{C_1} + \dfrac{1}{C_2}###
Substitute the values:
###\dfrac{1}{C_{eq}} = \dfrac{1}{2} + \dfrac{1}{4} = \dfrac{2}{4} + \dfrac{1}{4} = \dfrac{3}{4}###
So:
###C_{eq} = \dfrac{4}{3} \,\mu F \approx 1.33\,\mu F###
Parallel Combination
For capacitors in parallel, the equivalent capacitance is the direct sum:
###C_{eq} = C_1 + C_2 = 2 + 4 = 6 \,\mu F###
Conclusion
Equivalent capacitance in series: ##1.33 \,\mu F##
Equivalent capacitance in parallel: ##6 \,\mu F##
This demonstrates how series connection reduces total capacitance, while parallel connection increases it. Knowing these rules is crucial for analyzing capacitor networks in **IIT JEE circuit problems**..
Key Takeaways
Mastering capacitance is essential for success in the IIT JEE examination. Understanding the formulas, recognizing the factors affecting capacitance, and practicing numerical problems are key steps. With consistent effort and the right approach, you can conquer even the most challenging capacitor problems. This final section summarizes key points and offers encouragement for your preparation.
Summary of Key Concepts
Capacitance is the ability of a capacitor to store charge, defined by:
###C = \dfrac{Q}{V}###
For a parallel-plate capacitor, the capacitance depends on geometry and separation:
###C = \dfrac{\varepsilon_0 \cdot A}{d}###
When multiple capacitors are combined, their equivalent capacitance depends on the configuration:
- Series: ###\dfrac{1}{C_{eq}} = \dfrac{1}{C_1} + \dfrac{1}{C_2} + \dots### Equivalent capacitance is always less than the smallest capacitor in the set.
- Parallel: ###C_{eq} = C_1 + C_2 + \dots### Equivalent capacitance is the direct sum, larger than any individual capacitor.
These principles are essential for understanding how capacitors behave in circuits. Practice is key — mastering these concepts will strengthen your problem-solving skills and enhance your performance in the IIT JEE capacitance section.
Always remember to analyze the problem carefully, identify the given parameters, and choose the appropriate formula. Practice a variety of problems, including series and parallel combinations, to solidify your understanding. Consistent practice and a clear understanding of the underlying principles will build confidence. Review your work and seek help when needed. This diligent approach will prepare you for success in your IIT JEE examination. Remember, success in physics is a journey of understanding and practice.
Similar Problems (Quick Solutions)
Problem 1
Two capacitors of 3 µF and 6 µF are connected in series. Find the equivalent capacitance. Answer: 2 µF
Problem 2
A parallel-plate capacitor has plates of area 0.5 m² and a separation of 0.02 m. Find its capacitance (##ε₀## = 8.85 × 10⁻¹² F/m). Answer: 2.21 × 10⁻¹⁰ F
Problem 3
Three capacitors of 1 µF, 2 µF, and 3 µF are connected in parallel. Find the equivalent capacitance. Answer: 6 µF
Problem 4
A capacitor stores 10 µC of charge at 5 V. What is its capacitance? Answer: 2 µF
Problem 5
Two capacitors, 4 µF and 8 µF, are connected in series. Calculate the equivalent capacitance. Answer: 2.67 µF
| Concept | Formula | Description |
|---|---|---|
| Capacitance | ##C = Q/V## | Capacitance is the ratio of charge to voltage. |
| Parallel-Plate Capacitor | ##C = ε₀ * A / d## | Capacitance of a parallel plate capacitor depends on area and distance. |
| Capacitors in Series | ##1/C_eq = 1/C1 + 1/C2## | The reciprocal of equivalent capacitance is the sum of the reciprocals of individual capacitances. |
| Capacitors in Parallel | ##C_eq = C1 + C2## | The equivalent capacitance is the sum of individual capacitances. |
We also Published
RESOURCES
- Capacitors and Capacitance -Study Material for IIT JEE | askIITians
- Advanced Problems : Current Electricity and Capacitance for IIT JEE …
- Are there any tips to master electrostatics and capacitors for IIT …
- Capacitors : Theory Lectures for IIT JEE PHYSICS & NEET – YouTube
- CONTENTS
- JKs : IIT-JEE Q. 83 The capacitance of a parallel plate capacitor is …
- ELECTRIC POTENTIAL AND CAPACITANCE
- Capacitor | Physics | JEE Main Previous Year Questions …
- IIT JEE Physics Formula Revision – Ch. 31. Capacitors
- Electrostatic Potential and Capacitance Iit Jee | PDF | Dielectric …






0 Comments