General aptitude often hinges on solving number series problems, which test your ability to spot patterns and think logically. In this sequence, each term builds on the previous one through a clear mathematical relationship, offering a perfect exercise for sharpening your analytical skills.
Table of Contents
Read More
Number series problems are a cornerstone of general aptitude tests, designed to sharpen logical reasoning and pattern recognition skills. The sequence 2, 6, 12, 20, 30 presents a classic challenge that often appears in competitive exams, requiring a keen eye for numerical relationships.
Decoding the Pattern in Number Sequences
Unraveling number series isn’t just about finding the next term; it’s about understanding the underlying mathematical structure that governs the progression.
Identifying the Differences
Calculate the differences between consecutive terms: 6 – 2 = 4, 12 – 6 = 6, 20 – 12 = 8, 30 – 20 = 10. These differences form a sequence: 4, 6, 8, 10, which increases by 2 each time.
This consistent increment suggests a linear or quadratic pattern, common in many aptitude questions that test general numerical skills.
Formulating the General Term
Observing the terms: 2 = 1×2, 6 = 2×3, 12 = 3×4, 20 = 4×5, 30 = 5×6. Each term is the product of n and (n+1), where n starts at 1.
Thus, the nth term is n(n+1). For n=6, the next term should be 6×7 = 42, following this multiplicative pattern.
Applications in Aptitude Testing
Mastering such sequences is crucial for excelling in various competitive exams, where quick and accurate pattern recognition can make all the difference.
Enhancing Logical Thinking
Practicing number series improves deductive reasoning, as it forces the brain to identify rules and predict outcomes based on limited data.
This skill is transferable to real-world problem-solving, making it a valuable component of general aptitude assessments.
Common Variations and Pitfalls
Not all series are straightforward; some may involve alternating patterns or more complex functions like Fibonacci sequences.
Always verify by checking multiple terms to avoid misinterpreting the pattern, a common mistake in high-pressure exam settings.
Key Takeaways
Number series like 2, 6, 12, 20, 30 teach us to look for multiplicative or additive patterns. The missing term is 42, derived from n(n+1). Regular practice boosts general aptitude, essential for success in tests and beyond.
| Term Position (n) | Term Value | Pattern Description |
|---|---|---|
| 1 | 2 | 1 × 2 |
| 2 | 6 | 2 × 3 |
| 3 | 12 | 3 × 4 |
| 4 | 20 | 4 × 5 |
| 5 | 30 | 5 × 6 |
| 6 | 42 | 6 × 7 (Missing Term) |
We also Published
RESOURCES
- General Aptitude Test – Aptitude-test.com
- General Aptitude Contract : r/AirForceRecruits
- The role of mind-wandering in measurements of general aptitude
- General Aptitude : r/AirForceRecruits
- Fairness in Employment Testing: Validity Generalization, Minority …
- ED164579 – Manual for the USES General Aptitude Test … – ERIC
- GA General Aptitude
- Aptitude Questions and Answers – GeeksforGeeks
- Does anyone have General Aptitude in the Air Force?
- ASVAB – U.S. Air Force
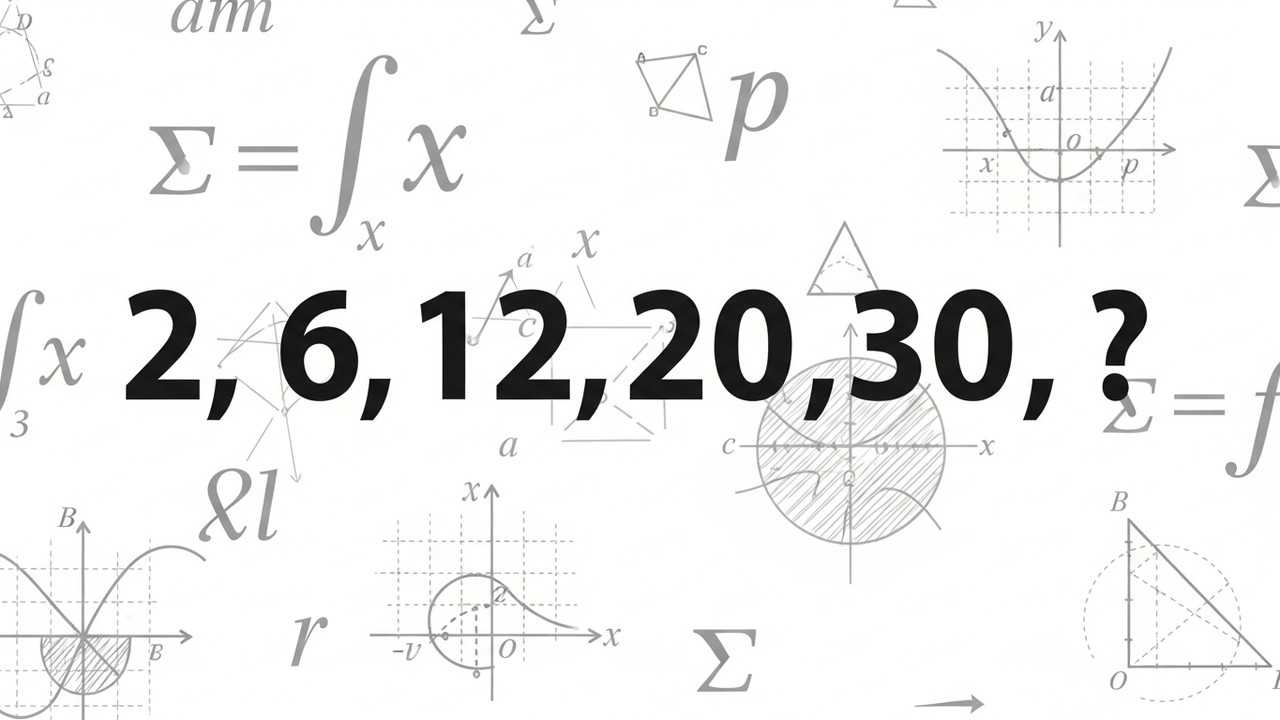







0 Comments