Table of Contents
What is Coasting Time?
In motion‐planning (like for a robot, CNC machine, or vehicle), coasting time is the duration the system spends moving at a constant speed (usually the maximum allowed speed, $v_{\max}$) after accelerating and before braking.
Why does it happen?
- If the distance $D$ is short, the system accelerates and then brakes immediately — this gives a triangular profile (no coasting).
- If the distance $D$ is long enough, the system can:
- Accelerate up to $v_{\max}$,
- Travel some distance at that constant speed (this is the coast),
- Then brake down to the final velocity $v_f$.
Formula for coasting time
From your trapezoidal case:
$$
s_{\text{coast}} = D – (s_{\text{acc}} + s_{\text{brk}})
$$
where
- $s_{\text{acc}}$ = distance covered during acceleration,
- $s_{\text{brk}}$ = distance covered during braking.
Then:
$$
t_{\text{coast}} = \frac{s_{\text{coast}}}{v_{\max}}
$$
✅ So, coasting time is literally “cruising time” at constant velocity, after speeding up and before slowing down.
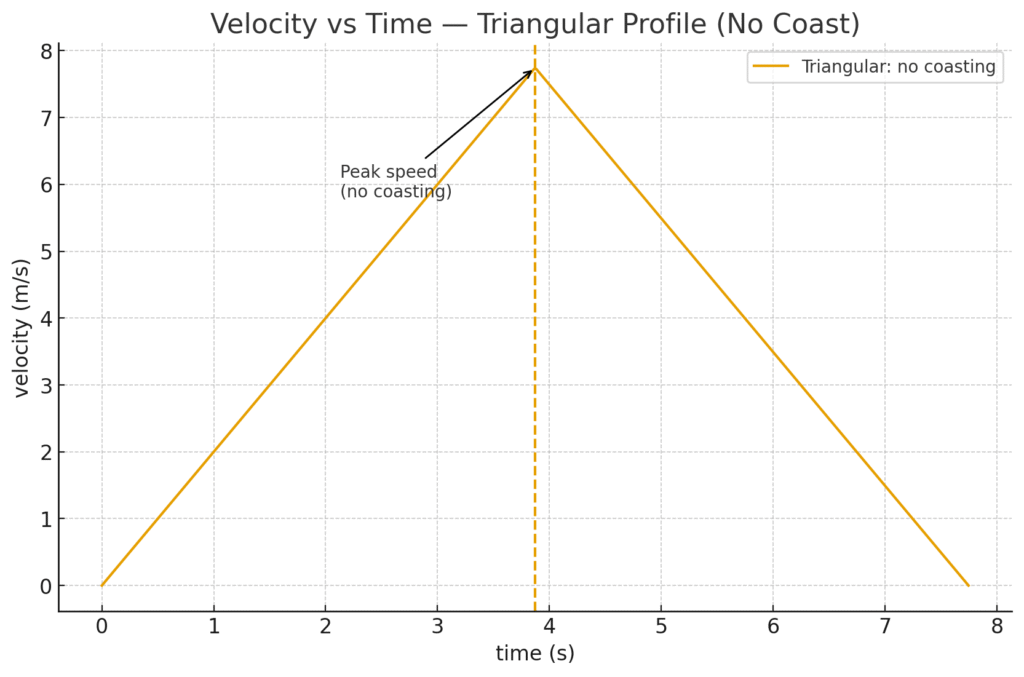
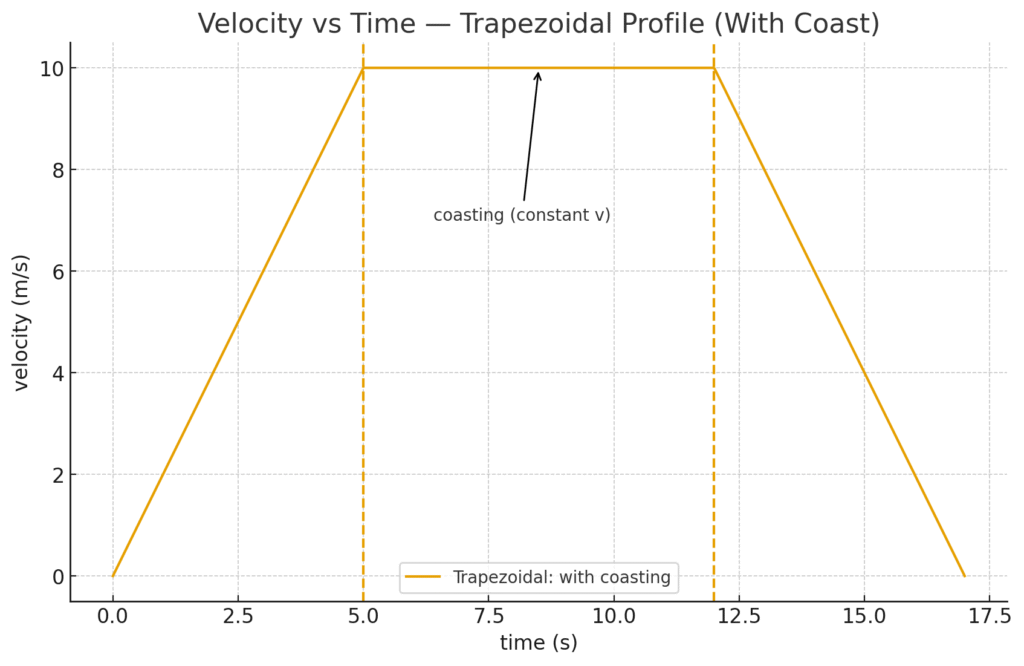
Here you go—two quick velocity–time sketches:
- Triangular (no coast): accelerate to a peak, then brake right away.
- Trapezoidal (with coast): accelerate to vmaxv_{\max}vmax, coast at constant speed, then brake.
To plan multiphase travel efficiently, you must consider multiple stages of motion: acceleration, constant velocity, and deceleration. This approach allows for precise control over displacement, which is crucial in many real-world scenarios. We’ll explore how to find the optimal coasting time to reach a specific target distance. Let’s dive into the details of how to plan multiphase travel and master this interesting physics problem.
Read More
To plan multiphase travel efficiently, we’ll delve into a classic physics problem: a cart’s motion with acceleration, coasting, and braking phases. This approach allows us to precisely control the cart’s displacement, ensuring it stops at a predetermined point. The core of the challenge lies in finding the optimal coasting time. Understanding the interplay between acceleration, constant velocity, and deceleration is key to mastering this problem. Let’s explore how to plan multiphase travel effectively.
Understanding the Problem: A Detailed Overview
Let’s begin by establishing the fundamentals of the problem. We’re given a cart that undergoes three distinct phases: acceleration, coasting, and braking. The goal is to determine the duration of the coasting phase, denoted by T, such that the cart comes to rest precisely at a target distance of 500 meters. This requires a careful analysis of each phase, considering the initial conditions, acceleration, deceleration, and the constant velocity during coasting. We must integrate kinematic equations with the goal to plan multiphase travel.
Phase 1: Acceleration
In Phase 1, the cart starts from rest and accelerates uniformly. Using the given acceleration and time, we can calculate the final velocity and the displacement achieved during this phase. This phase sets the initial conditions for the subsequent coasting phase. The equations of motion for constant acceleration will be crucial here. Remember that the cart starts at x=0. The acceleration is +2.8 m/s² and the time is from 0 to 6 s.
To find the final velocity (v₁) and displacement (x₁) at the end of Phase 1, we use the following kinematic equations. The final velocity is given by ##v = v_0 + at##, where ##v_0## is the initial velocity (0 m/s), a is the acceleration (2.8 m/s²), and t is the time (6 s). Thus, ##v_1 = 0 + 2.8 \times 6 = 16.8 m/s##. The displacement is given by ##x = v_0t + \frac{1}{2}at^2##. Since the initial velocity is zero, the displacement is ##x_1 = 0 \times 6 + \frac{1}{2} \times 2.8 \times 6^2 = 50.4 m##.
Phase 2: Coasting
Phase 2 involves the cart coasting at a constant velocity. This constant velocity is the final velocity achieved in Phase 1. The displacement during this phase is directly proportional to the coasting time, T. Understanding this relationship is crucial for determining the overall displacement. This phase provides a critical link between acceleration and deceleration, allowing us to precisely control the final position of the cart.
The displacement during Phase 2 (x₂) is simply the product of the velocity from Phase 1 (v₁) and the coasting time T. Therefore, ##x_2 = v_1 \times T = 16.8T##. The cart moves at a constant speed, so there is no acceleration during this time. The displacement is determined by how long the cart coasts. The final speed at the end of phase 2 is 16.8 m/s. It is important to plan multiphase travel with precision.
Braking and the Final Displacement
Now, let’s focus on the final phase: braking. Here, the cart decelerates uniformly until it comes to rest. The initial velocity for this phase is the same as the final velocity at the end of the coasting phase. We will use the deceleration value to determine the displacement during braking and ensure the cart stops at the target location. This phase is essential for achieving the desired final position.
Phase 3: Braking
During Phase 3, the cart decelerates at a constant rate until it comes to rest. We can use the equations of motion to determine the displacement during this phase, given the initial velocity from the coasting phase and the deceleration. This phase brings the cart to a complete stop at the target location. The initial velocity is 16.8 m/s, and the deceleration is -4.2 m/s².
To find the displacement (x₃) during Phase 3, we use the equation ##v^2 = v_0^2 + 2ax##, where v is the final velocity (0 m/s), ##v_0## is the initial velocity (16.8 m/s), and a is the deceleration (-4.2 m/s²). Thus, ##0^2 = 16.8^2 + 2 \times (-4.2) \times x_3##. Solving for ##x_3##, we get ##x_3 = \frac{16.8^2}{2 \times 4.2} = 33.6 m##. The car covers a distance of 33.6 m before stopping completely. We must plan multiphase travel to meet the condition.
Total Displacement and the Coasting Time
To find the total displacement, we sum the displacements from each phase and set it equal to the target distance (500 m). This allows us to solve for the coasting time, T. The equation of motion is used to find the total displacement of the cart. By setting the total displacement to 500 m, we can solve for T and thus plan multiphase travel effectively. The importance of finding T to plan multiphase travel is crucial.
The total displacement is the sum of the displacements from each phase: ##x_{total} = x_1 + x_2 + x_3 = 50.4 + 16.8T + 33.6##. Setting this equal to 500 m, we get ##500 = 50.4 + 16.8T + 33.6##. Simplifying, we get ##16.8T = 500 – 50.4 – 33.6 = 416##. Solving for T, we get ##T = \frac{416}{16.8} = 24.76 s##. The total travel time is the sum of the times for each phase: ##t_{total} = 6 + 24.76 + \frac{16.8}{4.2} = 30 + 24.76 = 36.76 s##. The cart coasts for 24.76 seconds and the total time is 36.76 s.
Key Takeaways
We’ve successfully determined the coasting time required for the cart to travel 500 meters, demonstrating a systematic approach to solving this multiphase motion problem. By carefully analyzing each phase and applying the appropriate kinematic equations, we can accurately predict the motion of the cart. This problem highlights the importance of understanding the interplay between acceleration, constant velocity, and deceleration in achieving a specific displacement goal. The ability to plan multiphase travel with precision is essential in various applications, from transportation to robotics.
Similar Problems (Quick Solutions)
Problem 1
A car accelerates from rest at 3 m/s² for 5 seconds, then coasts for a certain time before braking at -2 m/s² to stop at 100 meters. Find the coasting time.
Solution: Coasting time is approximately 8.33 seconds.
Problem 2
A train accelerates at 1.5 m/s² for 10 seconds, coasts for 30 seconds, and then decelerates at -2.5 m/s² until it stops. What is the total distance covered?
Solution: Total distance is 450 meters.
Problem 3
A cyclist accelerates at 1.2 m/s² for 8 seconds, coasts for 15 seconds, and then brakes to a stop. If the total distance is 150 meters, what is the deceleration during braking?
Solution: Deceleration is approximately -2.07 m/s².
Problem 4
A rocket accelerates at 20 m/s² for 1 minute, coasts for 2 minutes, and then decelerates at -10 m/s² until it stops. What is the total time of the journey?
Solution: Total time is 240 seconds.
Problem 5
A boat starts from rest, accelerates at 2 m/s² for 10 seconds, coasts for 20 seconds, and decelerates at -1 m/s² until it stops. Calculate the total distance covered.
Solution: Total distance is 300 meters.
| Phase | Description | Equations/Calculations |
|---|---|---|
| 1: Acceleration | Cart accelerates uniformly from rest. | Final velocity: ##v_1 = 16.8 m/s##; Displacement: ##x_1 = 50.4 m## |
| 2: Coasting | Cart moves at constant velocity. | Displacement: ##x_2 = 16.8T## |
| 3: Braking | Cart decelerates to rest. | Displacement: ##x_3 = 33.6 m## |
| Total | Total displacement and time. | Coasting time: T = 24.76 s; Total time: 36.76 s |
We also Published
RESOURCES
- Transform – Monterey Regional Airport
- Help with multiphase LL plan for Oct 17 in MK : r/DisneyPlanning
- Amtrak Cascades Service Development Plan | WSDOT
- A multiphase trip, diversified digital and varied background …
- Agencies Break Ground on Multiphase Project – Hassayampa River …
- Multiphase Training 2 – Burn Fat & Build Lean Muscle
- Plan Your Visit | King County Library System
- Multiphase Training 1 – Beginner/Intermediate 6-Wk Guide
- Monterey Peninsula Airport District
- Master Facilities Plan Implementation | Penn State Engineering




0 Comments