Evaluating limits is a fundamental concept in calculus, and understanding how to approach them is crucial for mastering the subject. The process of evaluating limits by direct substitution is often the first technique students learn. This method allows us to determine the behavior of a function as its input approaches a specific value, making it a building block for more complex calculus concepts. This blog post will explain and demonstrate how to evaluate limits using direct substitution.
On This Page
Read More
Understanding limits is fundamental in calculus. One of the simplest methods for evaluating limits involves direct substitution. This approach allows us to find the value a function approaches as its input approaches a specific value. In this article, we will explore the concept of evaluating limits by direct substitution, providing clear examples and explanations to enhance your understanding. The SEO Keyphrase, evaluating limits, will be central to our discussion.
Understanding Evaluating Limits
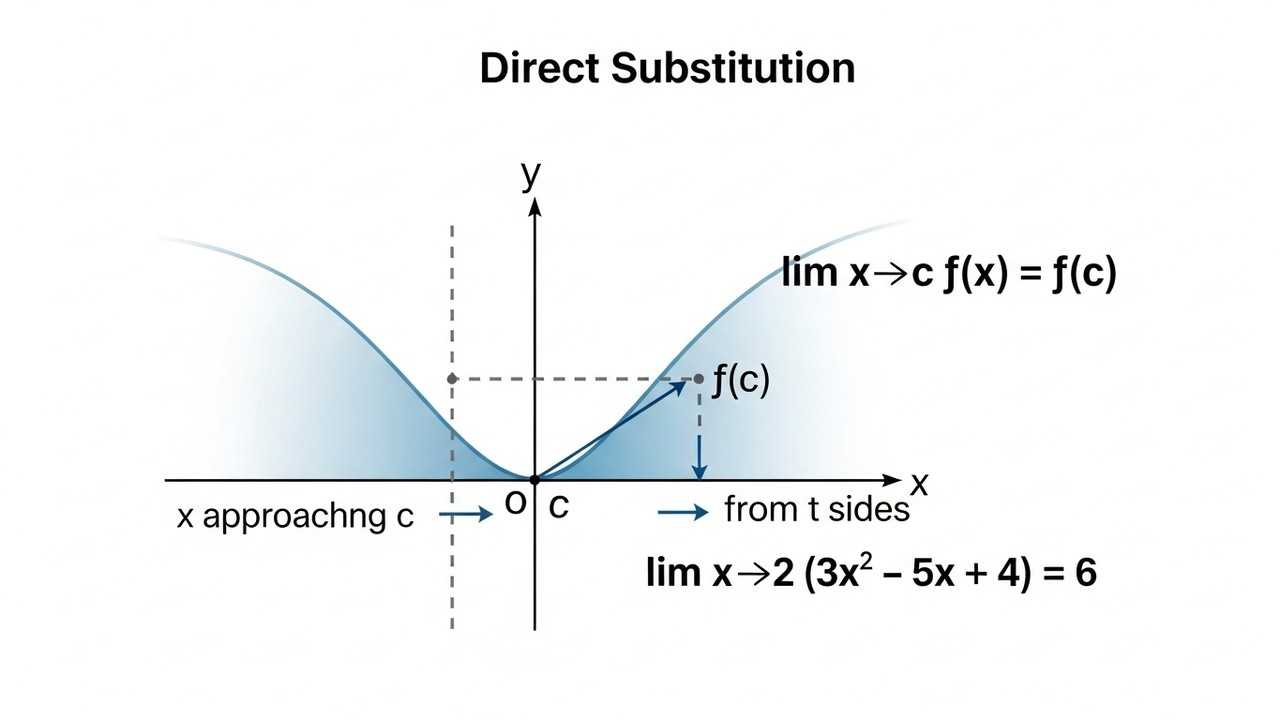
The process of evaluating limits often begins with direct substitution, where the value that x approaches is directly plugged into the function. This method works well for continuous functions. These functions do not have any breaks or jumps. The function's value at the point where the limit is taken is equal to the limit itself.
However, direct substitution isn't always applicable. If substituting the value results in an indeterminate form like 0/0, further analysis is needed. Such cases often require techniques like factoring, rationalizing, or applying L'Hôpital's rule. These methods will be crucial when direct substitution fails.
Direct Substitution Explained
When evaluating limits by direct substitution, we replace the variable (usually x) with the value it approaches. This method is straightforward for polynomial functions. We simply substitute the value into the function. The result is the limit itself. This is a basic but vital concept in calculus.
For example, to evaluate ## lim_{x \to 2} (3x^2 - 5x + 4)##, we substitute x = 2 into the expression ##3x^2 - 5x + 4##. The direct substitution gives us the limit. This is the simplest way to find limits, but it's not always the correct approach.
Step-by-Step Solution
Step 1: Direct Substitution
Substitute x = 2 into the function: ##3(2)^2 - 5(2) + 4##. This is the first step. This step is simple, but it's critical. It sets the stage for evaluating limits. This approach is effective when the function is continuous at the point where the limit is evaluated.
Step 2: Calculation
Calculate the expression: ##3(4) - 10 + 4 = 12 - 10 + 4 = 6##. We perform the arithmetic operations to find the final value. The result is the limit of the function as x approaches 2. This result directly answers the problem statement.
Final Solution
Therefore, ## lim_{x \to 2} (3x^2 - 5x + 4) = 6##. The limit exists and equals 6. This means as x gets closer and closer to 2, the function's value approaches 6. The process of evaluating limits is now complete.
Similar Problems and Quick Solutions
Problem 1: Evaluate ## lim_{x \to 1} (2x + 3)##
Solution: 5
Problem 2: Find ## lim_{x \to 0} (x^3 - 2x + 1)##
Solution: 1
Problem 3: Evaluate ## lim_{x \to -1} (x^2 + 3x - 2)##
Solution: -4
Problem 4: Find ## lim_{x \to 3} (4x - 7)##
Solution: 5
Problem 5: Evaluate ## lim_{x \to 2} (x^2 + 2x + 1)##
Solution: 9
| Concept | Explanation | Example |
|---|---|---|
| Evaluating Limits | Finding the value a function approaches as the input approaches a certain value. | ##\lim_{x \to a} f(x)## |
| Direct Substitution | Substituting the value that x approaches directly into the function. This is how we evaluate limits. | For ##f(x) = 3x^2 - 5x + 4## and ##x \to 2##, substitute 2 for x. |
| Continuous Functions | Functions where direct substitution is applicable. | Polynomial functions are usually continuous. |
We also Published
RESOURCES
- Evaluating Limits By Factoring - YouTube
- Limits - Evaluating
- Evaluating Limits - Basic Calculus - YouTube
- Calculus I - Computing Limits
- How to Find Any Limit (NancyPi) - YouTube
- [Calculus 1] Evaluating limits : How would you evaluate this limit? : r ...
- Evaluating Limits in Maths: Methods, Formulas & Examples
- Evaluating limits : r/learnmath
- Limit Calculator
- With limits/in general, why do you have to factor before evaluating ...




1 Comment