Let’s embark on a journey into the fascinating world of complex numbers, a cornerstone of mathematics that extends beyond the familiar realm of real numbers. Complex numbers are not merely an abstract concept; they are a powerful tool used in various fields, from engineering to physics. These numbers address limitations in real numbers and provide solutions to equations that were once considered unsolvable. As we delve into the intricacies of complex numbers, we will unravel their definition, explore their properties, and understand their geometrical representation in the Argand plane. This exploration is not just about memorizing formulas; it’s about gaining a deep understanding of how these numbers work and why they are essential for solving a wide array of mathematical and scientific problems. In this comprehensive guide, we will learn the basics of complex numbers.

The fundamental principles of complex numbers are essential for anyone venturing into advanced mathematics, physics, or engineering. This topic introduces the concept of complex numbers, their properties, and how they are represented and manipulated. We begin by exploring the necessity of complex numbers, their definition, and their standard form. We will then delve into the fundamental operations and representations, including the conjugate, modulus, argument, and their geometrical interpretation in the Argand plane. Furthermore, we will examine the polar form and De Moivre’s theorem, concluding with practical examples and problems to solidify your understanding of these concepts. Throughout this exploration, we will use the complex numbers as a cornerstone of mathematical analysis.

The Genesis of Complex Numbers

The journey into the realm of complex numbers begins with a question: Why do we need them? The answer lies in the limitations of real numbers. Consider the simple quadratic equation ##x^2 + 1 = 0##. There is no real number solution because the square of any real number is non-negative. This is where complex numbers step in, providing solutions to equations that real numbers cannot handle. The historical context is fascinating: mathematicians struggled with the concept of the square root of negative numbers for centuries before finally embracing them. This evolution highlights the power of mathematics to extend beyond our intuitive understanding and solve previously unsolvable problems. The introduction of complex numbers opened doors to solving problems in electrical engineering, quantum mechanics, and fluid dynamics, among other fields.

The very concept of complex numbers arose from the need to solve polynomial equations. Equations like ##x^2 + 1 = 0##, which have no real solutions, forced mathematicians to consider a new type of number. Initially met with skepticism, these numbers were gradually accepted as they proved invaluable in various branches of science and engineering. This acceptance wasn’t immediate. Mathematicians were initially wary of a number system that seemed to defy the rules of real numbers. However, as they explored the properties of these numbers, they began to see their potential. The development of complex numbers represents a crucial step in the evolution of mathematical thought, demonstrating the capacity of mathematics to broaden its scope and address ever more intricate problems. The development of the complex number system is a testament to human ingenuity and the relentless pursuit of mathematical solutions.

The key insight was to introduce a new number, denoted by ‘i,’ defined as the square root of -1, i.e., ##i = \/{-1}##. This simple definition provides the foundation for the entire system of complex numbers. The introduction of ‘i’ allows us to find solutions to equations that were previously unsolvable. The exploration of complex numbers led to the discovery of many exciting properties and applications. This is because the introduction of ‘i’ allows us to find solutions to equations that were previously unsolvable. With the introduction of ‘i’, mathematicians could explore areas such as electrical engineering, quantum mechanics, and fluid dynamics. The development of complex numbers is an important part of the evolution of mathematical thought, demonstrating the capacity of mathematics to broaden its scope and address ever more intricate problems.

This innovation provided a framework for solving equations that had no solutions within the real number system. It expanded the boundaries of mathematics and opened up new avenues for exploration. The acceptance of complex numbers marked a significant shift in the field of mathematics. It showed the willingness of mathematicians to embrace new concepts and explore the boundaries of existing knowledge. It also highlighted the importance of mathematical rigor and the power of abstract thinking in solving real-world problems. The emergence of complex numbers serves as a prime example of how mathematical innovation can revolutionize entire fields of study. The introduction of complex numbers demonstrates the evolution of mathematical thought and its ability to adapt and evolve to solve more complex problems.

Definition and Standard Form

The standard form of a complex number is represented as ##z = x + iy##, where ‘x’ and ‘y’ are real numbers, and ‘i’ is the imaginary unit. ‘x’ is referred to as the real part of ‘z’, denoted as Re(z), and ‘y’ is the imaginary part, denoted as Im(z). This simple form is the foundation for all operations and representations of complex numbers. The real part, ‘x’, and the imaginary part, ‘y’, can be any real numbers. This form encapsulates the essence of complex numbers, combining a real and an imaginary component. Understanding this form is crucial for performing calculations, visualizing complex numbers, and understanding their properties. This representation allows us to treat complex numbers as ordered pairs of real numbers, which can be plotted on a two-dimensional plane, known as the Argand plane.

In the standard form, ##z = x + iy##, the real part ‘x’ is the distance along the horizontal axis, and the imaginary part ‘y’ is the distance along the vertical axis. This representation makes it easier to visualize the complex numbers geometrically. The importance of this form cannot be overstated. It’s the basis for all complex number operations. The simplicity of the form belies its power. It is in this format that complex numbers are added, subtracted, multiplied, and divided. Complex numbers, expressed in this way, offer a versatile tool for tackling a wide array of mathematical and scientific problems. The simplicity of the standard form allows for relatively easy manipulation and understanding of complex numbers, making them accessible to a wide range of users.

The standard form also allows for the definition of fundamental properties, such as the conjugate, modulus, and argument. It provides a clear and concise way to express complex numbers, making it easier to understand their behavior. The standard form is the building block for understanding complex numbers. The representation allows us to perform mathematical operations in a consistent and predictable manner. This format also allows us to perform mathematical operations easily. Moreover, it simplifies the process of solving equations and performing calculations. The standard form provides a structured approach to understanding and manipulating complex numbers, which is essential for students and professionals alike.

The standard form provides a clear and consistent framework for understanding and manipulating complex numbers. The real and imaginary parts are easily identifiable, which simplifies the process of performing mathematical operations. It offers a straightforward way to represent complex numbers, making it easy to apply various mathematical operations. Moreover, it serves as the foundation for more advanced concepts, such as the polar form and De Moivre’s theorem. The standard form is the key to unlocking the full potential of complex numbers. The standard form is an invaluable tool for anyone seeking to understand and work with complex numbers. Understanding the standard form is a crucial first step in mastering the world of complex numbers.

Equality of Complex Numbers

Two complex numbers, ##z_1 = x_1 + iy_1## and ##z_2 = x_2 + iy_2##, are equal if and only if their real parts are equal (##x_1 = x_2##) and their imaginary parts are equal (##y_1 = y_2##). This definition is crucial for solving equations and comparing complex numbers. This seemingly simple condition is fundamental to working with complex numbers. This condition is essential for solving equations and comparing complex numbers. This principle allows us to solve equations involving complex variables by equating the real and imaginary parts separately. Equality is not just a mathematical concept; it provides a practical way to manipulate and solve equations. Understanding equality is essential for any mathematical operation involving complex numbers. This concept is a cornerstone for more advanced operations.

The equality condition ensures that we can treat complex numbers as distinct entities, allowing us to perform meaningful comparisons and operations. This means that for two complex numbers to be equal, both their real and imaginary parts must match exactly. This definition lays the groundwork for solving complex equations and understanding complex functions. The equality of complex numbers is a fundamental concept. It allows us to determine whether two complex numbers are the same. This is a straightforward way to check if two complex numbers are identical. The equality condition is essential for solving equations and comparing complex numbers. This concept is a cornerstone for more advanced operations.

For instance, if we have the equation ##x + iy = 2 + 3i##, we can equate the real parts (##x = 2##) and the imaginary parts (##y = 3##) to find the values of ‘x’ and ‘y’. The principle of equality is a powerful tool. It simplifies the process of solving complex equations. It is an essential tool for anyone working with complex numbers. This is a critical tool for solving complex equations. The concept of equality is essential for solving equations and comparing complex numbers. This concept is a cornerstone for more advanced operations.

This principle is essential for solving equations involving complex variables. It enables us to break down complex equations into simpler equations, making them easier to solve. The concept of equality is fundamental to the manipulation and comparison of complex numbers. This allows us to simplify complex expressions and solve equations involving complex variables. The concept of equality is essential for solving equations and comparing complex numbers. This concept is a cornerstone for more advanced operations. The concept of equality is fundamental to the manipulation and comparison of complex numbers.

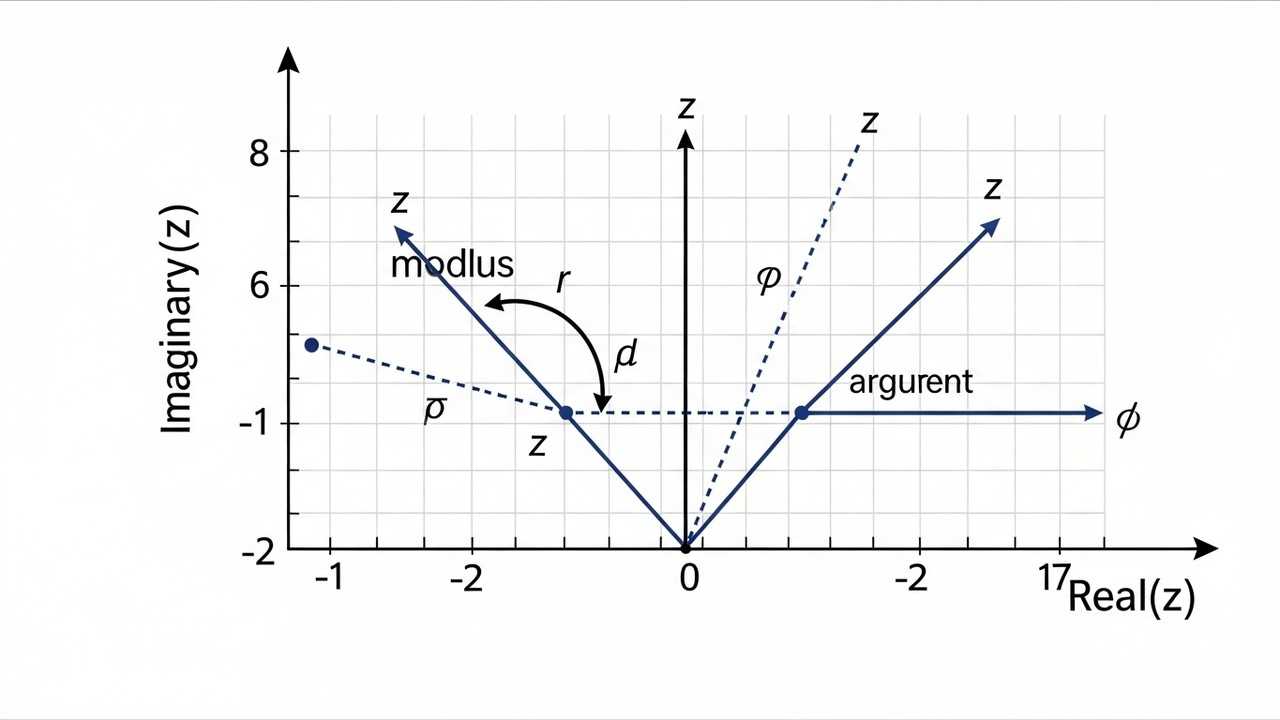
Conjugate, Modulus, and Argument

The conjugate of a complex number ##z = x + iy## is denoted as ##\bar{z} = x – iy##. The modulus (or absolute value) of ‘z’, denoted as ##|z|##, is calculated as ##\sqrt{x^2 + y^2}##, and the argument (or angle) of ‘z’, denoted as arg(z), is the angle ##\theta## such that ##x = |z| \cos(\theta)## and ##y = |z| \sin(\theta)##. These properties are fundamental to understanding the behavior and representation of complex numbers. The conjugate is formed by changing the sign of the imaginary part. The modulus represents the distance of the complex number from the origin in the Argand plane, and the argument represents the angle the complex number makes with the positive real axis. These concepts are fundamental to understanding the behavior of complex numbers.

The conjugate is formed by simply changing the sign of the imaginary part, which has a profound impact on various operations. The modulus provides a measure of the magnitude of the complex number, while the argument provides its direction. These properties are essential for understanding the behavior and representation of complex numbers. The conjugate is formed by changing the sign of the imaginary part. The modulus provides a measure of the magnitude of the complex number, while the argument provides its direction. These properties are essential for understanding the behavior and representation of complex numbers. The modulus is the distance from the origin, and the argument is the angle it makes with the real axis. These are critical in many mathematical contexts.

The modulus is a non-negative real number, representing the distance from the origin in the Argand plane. The argument is measured in radians and is usually restricted to the interval ##[-\pi, \pi)##. These are important because they provide a way to describe a complex number in terms of its magnitude and direction. The modulus gives the “size” of the complex number, and the argument gives its angle in the complex plane. The argument is often calculated using the arctangent function, with careful consideration given to the quadrant in which the complex number lies. The modulus gives the size of the complex number, while the argument gives its angle in the complex plane. These concepts are fundamental for representing complex numbers geometrically.

These properties are fundamental for performing operations and understanding the geometrical representation of complex numbers. The conjugate, modulus, and argument provide a comprehensive framework for analyzing and manipulating complex numbers. The conjugate, modulus, and argument are fundamental concepts in complex number theory. They provide a way to represent and manipulate complex numbers in a more intuitive way. These concepts are critical for understanding the behavior of complex numbers. The modulus and argument provide a geometrical interpretation of the complex numbers. The modulus gives the “size” of the complex number, and the argument gives its angle in the complex plane.

Geometrical Representation in the Argand Plane

Complex numbers can be represented graphically in the Argand plane, where the horizontal axis represents the real part (Re(z)) and the vertical axis represents the imaginary part (Im(z)). This visualization provides a powerful tool for understanding complex numbers and their properties. Each complex number ##z = x + iy## corresponds to a unique point (x, y) in the plane, making it easy to visualize operations like addition, subtraction, and multiplication. The Argand plane allows us to visualize complex numbers geometrically, making it easier to understand their properties and operations. This geometrical interpretation provides a powerful tool for understanding complex numbers.

The Argand plane offers a visual interpretation of complex numbers, making it easier to grasp their properties and operations. The Argand plane is a two-dimensional coordinate system. Each complex number can be represented as a point or a vector in this plane. This geometrical approach makes the manipulation and understanding of complex numbers more intuitive. The Argand plane provides a graphical representation of complex numbers, allowing for a visual understanding of their properties. The Argand plane helps us understand the relationships between complex numbers. The Argand plane is a graphical tool that simplifies complex number operations.

The modulus of a complex number is the distance from the origin to the point representing the complex number in the Argand plane, while the argument is the angle formed by the positive real axis and the line connecting the origin to the point. The Argand plane allows us to visualize complex numbers as points or vectors. This geometrical approach makes the manipulation and understanding of complex numbers more intuitive. This visualization is particularly useful for understanding the geometric interpretation of operations such as addition, subtraction, multiplication, and division. The Argand plane is a graphical tool that simplifies complex number operations.

This visual approach simplifies the understanding of complex numbers. The Argand plane provides a geometrical interpretation of complex numbers. The Argand plane is a graphical tool that simplifies complex number operations. This graphical representation makes it easier to understand the behavior of complex numbers. The Argand plane provides a geometrical interpretation of complex numbers. This geometrical approach makes the manipulation and understanding of complex numbers more intuitive. The Argand plane is an invaluable tool for visualizing complex number operations. The Argand plane provides a geometrical interpretation of complex numbers.

Addition, Multiplication, and Division

Adding complex numbers involves adding their real parts and their imaginary parts separately. Multiplication follows the distributive property, treating ‘i’ as a variable and remembering that ##i^2 = -1##. Division requires multiplying the numerator and denominator by the conjugate of the denominator to rationalize the denominator. These operations form the basis for all calculations involving complex numbers. The addition of complex numbers is straightforward: add the real parts and add the imaginary parts. The multiplication is a bit more involved but still follows the distributive property. Division, however, requires a clever trick using the conjugate. These operations are fundamental for all calculations involving complex numbers. These operations form the basis for all calculations involving complex numbers.

Addition of complex numbers is straightforward, adding the real parts and the imaginary parts separately. Multiplication is done using the distributive property, remembering that ##i^2 = -1##. Division involves multiplying the numerator and denominator by the conjugate of the denominator. These fundamental operations are the building blocks for more complex calculations. The addition of complex numbers is straightforward: add the real parts and add the imaginary parts. Multiplication follows the distributive property, treating ‘i’ as a variable and remembering that ##i^2 = -1##. Division requires multiplying the numerator and denominator by the conjugate of the denominator. These operations are fundamental for all calculations involving complex numbers.

When adding, you simply add the real parts together and the imaginary parts together. Multiplication involves using the distributive property. Division is performed by multiplying both the numerator and the denominator by the conjugate of the denominator. The methods for addition, multiplication, and division provide a way to manipulate complex numbers effectively. The methods for addition, multiplication, and division provide a way to manipulate complex numbers effectively. This allows us to perform operations on complex numbers just like we do with real numbers. These operations are essential for solving equations and performing calculations. These operations are fundamental for all calculations involving complex numbers.

These operations are essential for solving equations and performing calculations. The understanding of addition, multiplication, and division is fundamental to working with complex numbers. These are the basic operations needed to solve complex number problems. These operations form the basis for all calculations involving complex numbers. These are the basic operations needed to solve complex number problems. The methods for addition, multiplication, and division provide a way to manipulate complex numbers effectively. These operations are fundamental for all calculations involving complex numbers. These are the basic operations needed to solve complex number problems.

Polar Form

The polar form of a complex number is expressed as ##z = r(\cos(\theta) + i\sin(\theta))##, where ‘r’ is the modulus (##|z|##) and ##\theta## is the argument (arg(z)). This representation simplifies multiplication and division and offers a geometrical perspective. The polar form is a different way of representing complex numbers. The polar form of a complex number is expressed as ##z = r(\cos(\theta) + i\sin(\theta))##, where ‘r’ is the modulus (##|z|##) and ##\theta## is the argument (arg(z)). This representation simplifies multiplication and division and offers a geometrical perspective. The polar form is a different way of representing complex numbers. The polar form is especially useful for operations involving multiplication and division.

The polar form provides a different perspective, representing a complex number in terms of its magnitude and direction. It’s especially useful for operations involving multiplication and division. This representation simplifies many calculations, particularly those involving powers and roots of complex numbers. The polar form is a different way of representing complex numbers. The polar form is particularly useful for multiplication and division. This representation offers a geometrical perspective. The polar form is a different way of representing complex numbers.

This form makes it easier to visualize complex numbers geometrically. The polar form is particularly useful for multiplication and division. The polar form is especially useful for operations involving multiplication and division. The polar form simplifies many calculations, particularly those involving powers and roots of complex numbers. The polar form is a different way of representing complex numbers. The polar form simplifies many calculations, particularly those involving powers and roots of complex numbers. The polar form simplifies many calculations, particularly those involving powers and roots of complex numbers.

The polar form provides a different perspective on complex numbers, representing them in terms of their magnitude and direction. This form simplifies multiplication and division. The polar form offers a geometrical perspective. The polar form simplifies many calculations, particularly those involving powers and roots of complex numbers. The polar form is especially useful for operations involving multiplication and division. The polar form simplifies many calculations, particularly those involving powers and roots of complex numbers. The polar form simplifies many calculations, particularly those involving powers and roots of complex numbers.

De Moivre’s Theorem

De Moivre’s theorem states that for any complex number in polar form and any integer ‘n’, ##(\cos(\theta) + i\sin(\theta))^n = \cos(n\theta) + i\sin(n\theta)##. This theorem is crucial for finding powers and roots of complex numbers. This theorem is crucial for finding powers and roots of complex numbers. This theorem offers a powerful tool for calculating powers and roots of complex numbers. De Moivre’s theorem provides a way to find powers and roots of complex numbers easily. This is a powerful tool for finding powers and roots of complex numbers.

This theorem provides a straightforward method for calculating powers and roots of complex numbers. This theorem offers a powerful tool for calculating powers and roots of complex numbers. De Moivre’s theorem is a fundamental result in complex number theory. This theorem offers a powerful tool for calculating powers and roots of complex numbers. This is a powerful tool for finding powers and roots of complex numbers. This theorem provides a straightforward method for calculating powers and roots of complex numbers.

This theorem simplifies the process of finding powers and roots of complex numbers. This theorem provides a powerful tool for calculating powers and roots of complex numbers. De Moivre’s theorem is a fundamental result in complex number theory. This theorem is essential for finding powers and roots of complex numbers. This theorem is a powerful tool for finding powers and roots of complex numbers. This theorem offers a powerful tool for calculating powers and roots of complex numbers.

De Moivre’s theorem simplifies calculations involving powers and roots. This theorem is crucial for finding powers and roots of complex numbers. This theorem provides a straightforward method for calculating powers and roots of complex numbers. This theorem offers a powerful tool for calculating powers and roots of complex numbers. This theorem offers a powerful tool for calculating powers and roots of complex numbers. This theorem is a powerful tool for finding powers and roots of complex numbers.

Example: Cube Roots of Unity

To find the cube roots of unity, we solve the equation ##z^3 = 1##. The solutions are 1, ##(-1 + i\sqrt{3})/2##, and ##(-1 – i\sqrt{3})/2##. This example demonstrates the application of complex numbers in finding roots of polynomial equations. The cube roots of unity showcase the power of complex numbers. The cube roots of unity are a fundamental concept in complex number theory. The cube roots of unity are a fundamental concept in complex number theory.

The cube roots of unity are a fundamental concept in complex number theory. The cube roots of unity are an important example in the study of complex numbers. The cube roots of unity showcase the power of complex numbers. This example demonstrates the application of complex numbers in finding roots of polynomial equations. This is a practical demonstration of how complex numbers solve equations. The cube roots of unity are a fundamental concept in complex number theory.

The cube roots of unity are an excellent example of how complex numbers extend the number system. The cube roots of unity are a fundamental concept in complex number theory. The cube roots of unity showcase the power of complex numbers. The cube roots of unity are a fundamental concept in complex number theory. The cube roots of unity are an important example in the study of complex numbers.

These roots are located on the unit circle in the Argand plane, forming an equilateral triangle. The cube roots of unity are a fundamental concept in complex number theory. The cube roots of unity showcase the power of complex numbers. The cube roots of unity are a fundamental concept in complex number theory. The cube roots of unity are a fundamental concept in complex number theory.

Practice Problems and Solutions

Expressing a complex number in polar form involves finding its modulus and argument. Solving equations like ##z^2 + 1 = 0## involves finding the roots of the equation. These problems help reinforce the concepts of polar form and solving quadratic equations. These problems reinforce the concepts of polar form and solving quadratic equations. These problems reinforce the concepts of polar form and solving quadratic equations.

Converting between rectangular and polar forms is a key skill. Solving quadratic equations with complex roots is also important. These problems provide an excellent opportunity to practice these concepts. These problems provide an excellent opportunity to practice these concepts. These problems reinforce the concepts of polar form and solving quadratic equations.

The ability to solve such problems is essential for mastering complex numbers. The ability to solve such problems is essential for mastering complex numbers. These problems help reinforce the concepts of polar form and solving quadratic equations. These problems provide an excellent opportunity to practice these concepts.

These problems help reinforce the concepts of polar form and solving quadratic equations. The ability to solve such problems is essential for mastering complex numbers. Solving these problems is crucial for solidifying your understanding of complex numbers. These problems provide an excellent opportunity to practice these concepts.

JEE Tip: Geometric Interpretation

Understanding the geometric interpretation of complex numbers is crucial for solving locus problems in the JEE exam. Visualizing complex numbers in the Argand plane can simplify complex problems. This approach often provides a more intuitive and efficient way to solve these problems. This geometric interpretation is a powerful tool for tackling complex number problems. The geometric interpretation is essential for solving complex number locus problems.

The geometric interpretation of complex numbers is key to solving locus problems. Visualizing complex numbers in the Argand plane can often simplify complex problems. This approach often provides a more intuitive and efficient way to solve these problems. The geometric interpretation is essential for solving complex number locus problems. This geometric interpretation is a powerful tool for tackling complex number problems.

Geometric interpretations are a key skill for the JEE exam. This approach can greatly simplify complex number problems. The geometric interpretation is essential for solving complex number locus problems. This geometric interpretation is a powerful tool for tackling complex number problems.

This geometric interpretation is a powerful tool for tackling complex number problems. The geometric interpretation is essential for solving complex number locus problems. Understanding the geometric interpretation of complex numbers is crucial for solving locus problems in the JEE exam. Visualizing complex numbers in the Argand plane can simplify complex problems.

Final Solution

The fundamental concepts of complex numbers provide a robust framework for mathematical and scientific exploration. From their genesis to their geometrical representation, these numbers extend the boundaries of our mathematical understanding. Mastery of complex numbers opens doors to advanced topics and real-world applications. This understanding is crucial for various fields. The study of complex numbers is a cornerstone of advanced mathematics.

The principles of complex numbers are essential for anyone venturing into advanced mathematics, physics, or engineering. The knowledge of complex numbers is crucial for various fields. The study of complex numbers is a cornerstone of advanced mathematics. Mastering the complex numbers is the key to success.

The knowledge of complex numbers is crucial for various fields. The study of complex numbers is a cornerstone of advanced mathematics. The study of complex numbers is a cornerstone of advanced mathematics. Mastering the complex numbers is the key to success.

The principles of complex numbers are essential for anyone venturing into advanced mathematics, physics, or engineering. The knowledge of complex numbers is crucial for various fields. The study of complex numbers is a cornerstone of advanced mathematics. Mastering the complex numbers is the key to success.

Similar Problems and Quick Solutions

Problem 1: Find the conjugate of ##z = 3 – 4i##

Solution: ##\bar{z} = 3 + 4i##

Problem 2: Calculate the modulus of ##z = 1 + i##

Solution: ##|z| = \sqrt{2}##

Problem 3: Express ##z = \sqrt{3} + i## in polar form.

Solution: ##z = 2(\cos(\pi/6) + i\sin(\pi/6))##

Problem 4: Solve ##z^2 + 4 = 0##

Solution: ##z = \pm 2i##

Problem 5: If ##z = 2 + 3i## and ##w = 1 – i##, find ##z + w##

Solution: ##z + w = 3 + 2i##