Complex numbers mastery invites you into a vibrant landscape where algebra and geometry converse on the complex plane. In this course, you will learn addition, subtraction, multiplication, and division of complex numbers, explore the radiant polar form, and savor the power of Euler’s formula. As you move from ##z = x + iy## to the elegant expressions ##r(\cos \theta + i \sin \theta)##, you’ll see De Moivre’s theorem transform daunting powers and root extractions into straightforward geometric actions. The journey weaves together theory, visualization, and practice problems to sharpen intuition and computational skill in the realm of complex numbers. Complex numbers mastery guides your progress with clarity and purpose.

Welcome to an exploration where algebra dances with geometry, and the complex plane becomes a vivid landscape of rotation, scaling, and hidden symmetry. Complex numbers mastery unfolds through familiar operations—addition, subtraction, multiplication, and division—then advances to the polar form and the unifying power of Euler’s formula. As you move from ##z = x + iy## to the elegant expressions ##r(\cos \theta + i \sin \theta)##, you’ll see De Moivre’s theorem transform daunting powers and root extractions into straightforward geometric actions. This post weaves together theory, visualization, and practical problems to sharpen intuition and computational skill in the realm of complex numbers.

Foundations of Complex Numbers

Algebraic Form and Conjugates

In the algebraic form, a complex number is written as ##z = x + iy## where ##x## and ##y## are real numbers and ##i## satisfies ##i^2 = -1##. The conjugate is ##\bar{z} = x – iy##, which flips the sign of the imaginary part and plays a pivotal role in division and magnitude calculations. When we multiply ##z## by its conjugate, we obtain a real, nonnegative quantity: ##z\bar{z} = x^2 + y^2 = |z|^2##. This identity underpins many steps in solving equations and in forming the modulus of complex expressions. The elementary operations—addition and subtraction—occur componentwise as expected: ##(a + ib) \pm (c + id) = (a \pm c) + i(b \pm d)##.

Understanding conjugates is not merely algebraic trivia; it’s a geometric tool. Conjugation corresponds to reflecting a point across the real axis in the Argand plane. This reflection preserves modulus but inverts the sign of the argument, a fact we’ll exploit when working with roots and locus problems. The interplay between ##z## and ##\bar{z}## clarifies why certain fractions and products produce real results, a recurring theme in complex analysis and applications.

The modulus ##|z| = \sqrt{x^2 + y^2}## measures distance from the origin, while the argument ##\arg(z)## provides the angle the vector makes with the positive real axis. These two quantities connect algebra and geometry and set the stage for polar representations. Mastery of conjugates and modulus equips you to simplify expressions rapidly and to anticipate how complex numbers behave under multiplication—an essential skill for higher-level topics.

As you practice, keep in mind the identity ##z\bar{z} = |z|^2## and use conjugates to rationalize denominators or to compute divisions. These ideas form the backbone of many solution strategies in problems ranging from polynomial equations to transformations in the complex plane.

Together, algebraic form and conjugates establish a sturdy foothold for venturing into polar coordinates and the powerful theorems that govern complex numbers.

Modulus and Argument

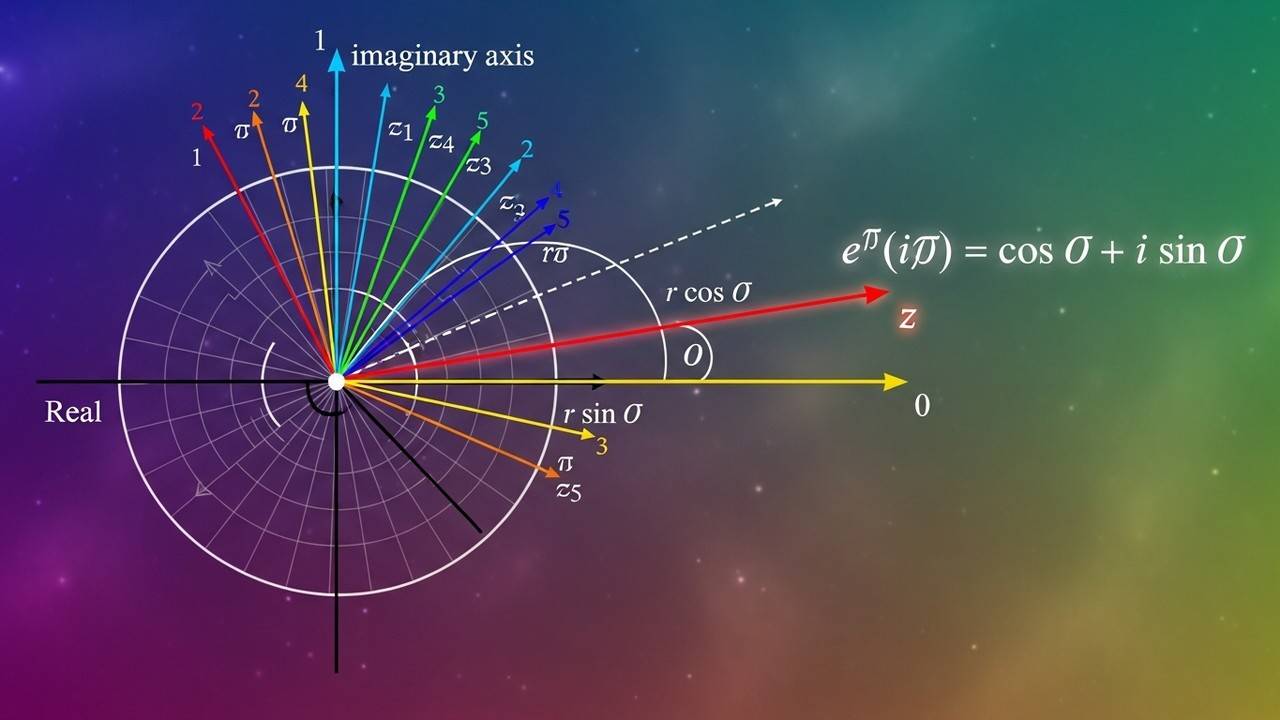
The modulus ##|z|## measures the distance from the origin to the point ##(x, y)## in the plane, computed as ##|z| = \sqrt{x^2 + y^2}##. The argument ##\arg(z)## is the angle that the vector from the origin to ##(x, y)## makes with the positive real axis, uniquely defined up to adding multiples of ##2\pi##. When a complex number is expressed in polar form, ##z = r(\cos \theta + i \sin \theta)##, the modulus is ##r## and the argument is ##\theta##. This representation reveals the geometric action of multiplication: magnitudes multiply and angles add, which is the key idea behind De Moivre’s theorem and efficient computation of powers and roots.

Converting between algebraic and polar forms is a central skill. Given ##z = x + iy##, you can obtain ##r## and ##\theta## via ##r = |z|## and ##\theta = \arg(z)## with attention to the quadrant of ##(x, y)##. Conversely, Euler’s formula, ###e^{i\theta} = \cos \theta + i \sin \theta###, bridges the trigonometric and exponential worlds, enabling compact representations and simpler calculus under complex exponentiation. In many problems, recognizing a complex number as ##r e^{i\theta}## or ##r(\cos \theta + i \sin \theta)## streamlines both symbolic manipulation and geometric intuition.

Calculating the argument requires care with branches; the principal value typically lies in ##(-\pi, \pi]##, but adding ##2\pi k## yields all possible angles for the same ##z##. Modulus is unambiguous and always nonnegative. When you compose these ideas, you gain a powerful lens for viewing complex numbers as points with radial distance and rotation, rather than as abstract symbols.

Polar Form and Euler’s Formula

Converting to Polar Form

To convert a complex number ##z = x + iy## to polar form, you compute ##r = |z| = \sqrt{x^2 + y^2}## and ##\theta = \arctan(y/x)## adjusted for the correct quadrant. With ##r## and ##\theta## in hand, ##z## can be written as ##z = r(\cos \theta + i \sin \theta)##. This polar representation emphasizes the geometric role of a complex number as a vector in the plane, whose length is ##r## and whose direction is ##\theta##. The polar form is particularly powerful for multiplication and division, because it turns these operations into simple additions or subtractions of angles and radii.

When a number lies on the unit circle, ##r = 1##, and ##z## reduces to ###e^{i\theta}### via Euler’s formula. The ability to express ##z## as ###e^{i\theta}### or ##\cos \theta + i \sin \theta## unifies trigonometry with complex exponentials and provides a clean pathway to higher powers and roots. In many problems, identifying a standard angle ##\theta##, such as ##\theta = \pi/2## or ##\theta = \pi/3##, immediately reveals the exact values of ##z## in polar form without lengthy calculations.

For a quick check, verify that ##x = r \cos \theta## and ##y = r \sin \theta## by back-substituting into ##z = x + iy##. This sanity check ensures you’ve chosen the correct quadrant and that your ##\theta## is consistent with the signs of ##x## and ##y##. The polar form also makes plotting and visualizing complex operations straightforward, as you’re following a rotation by ##\theta## and a scaling by ##r## rather than juggling a algebraic mix of ##x## and ##y## alone.