Solving problems involving ellipses often involves applying the concepts and equations we’ve discussed. Here are some common types of Ellipse Problems and how to approach them:

1. Finding the Equation of an Ellipse

This usually involves determining the center, the values of a and b (or a² and b²), and the orientation of the ellipse. Use the given information (vertices, foci, co-vertices, points on the ellipse, etc.) to find these values.

Example 1:

Find the equation of an ellipse with foci at (0, 2) and (0, -2) and a major axis length of 10.

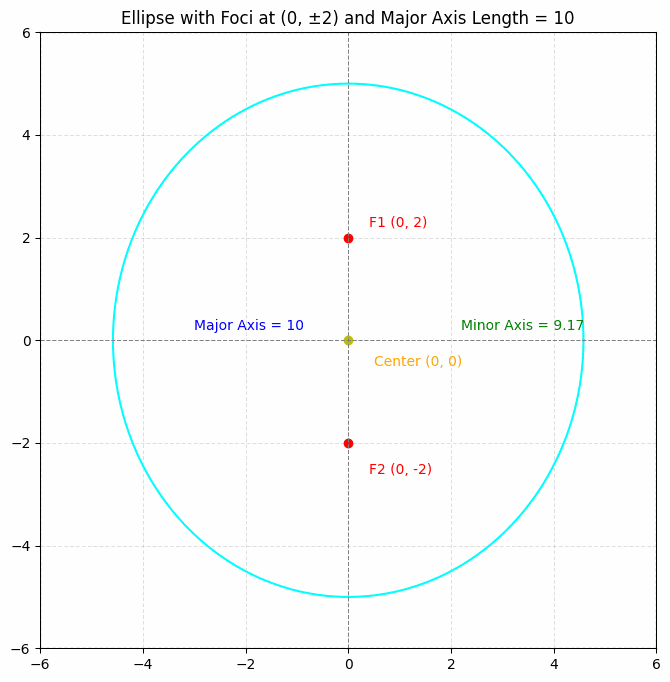
Solution:

The foci are at (0, 2) and (0, -2), so the center is at (0, 0) and the major axis is along the y-axis. The distance between the foci is 2c = 4, so c = 2. The major axis length is 2a = 10, so a = 5. We can find b using ##c^2 = a^2 – b^2##:

### 2^2 = 5^2 – b^2 ###### 4 = 25 – b^2 ###### b^2 = 21 ###### b = \sqrt{21} ###

Therefore, the equation of the ellipse is:

### \frac{x^2}{21} + \frac{y^2}{25} = 1 ###

2. Ellipse Problems on Finding the Foci, Vertices, and Co-vertices

Given the equation of an ellipse, identify the center, a, b, and the orientation. Then, use these values to calculate the coordinates of the foci, vertices, and co-vertices.

Example 2 (Ellipse Problems):

Find the foci, vertices, and co-vertices of the ellipse: ##\frac{(x + 4)^2}{16} + \frac{(y – 1)^2}{9} = 1##

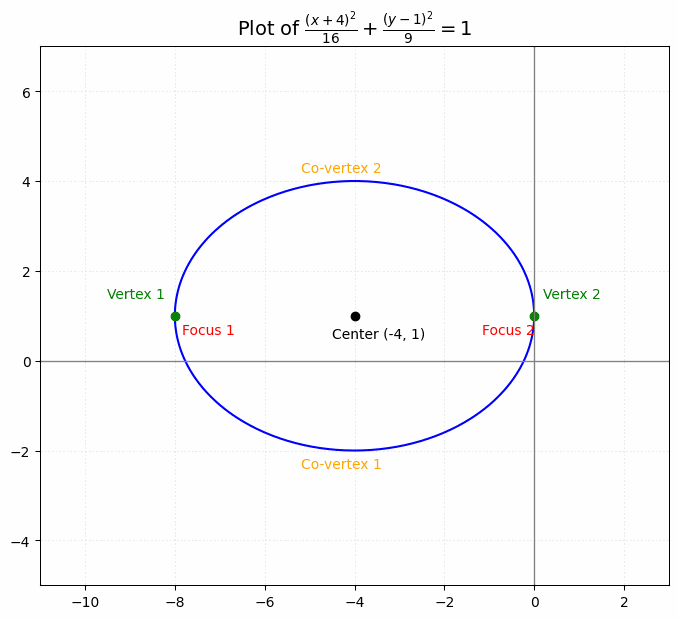
Solution:

The center is at (-4, 1). Since 16 is under the x-term, the major axis is horizontal. a² = 16, so a = 4. b² = 9, so b = 3. We can find c using ##c^2 = a^2 – b^2##:

### c^2 = 16 – 9 ###### c = \sqrt{7} ###

The vertices are at (-4 ± 4, 1), which are (0, 1) and (-8, 1). The co-vertices are at (-4, 1 ± 3), which are (-4, 4) and (-4, -2). The foci are at (-4 ± √7, 1).

3. Finding the Eccentricity

Once you know a and c, you can easily calculate the eccentricity using the formula ##e = \frac{c}{a}##.

Example 3:

Find the eccentricity of the ellipse: ##\frac{x^2}{25} + \frac{y^2}{9} = 1##

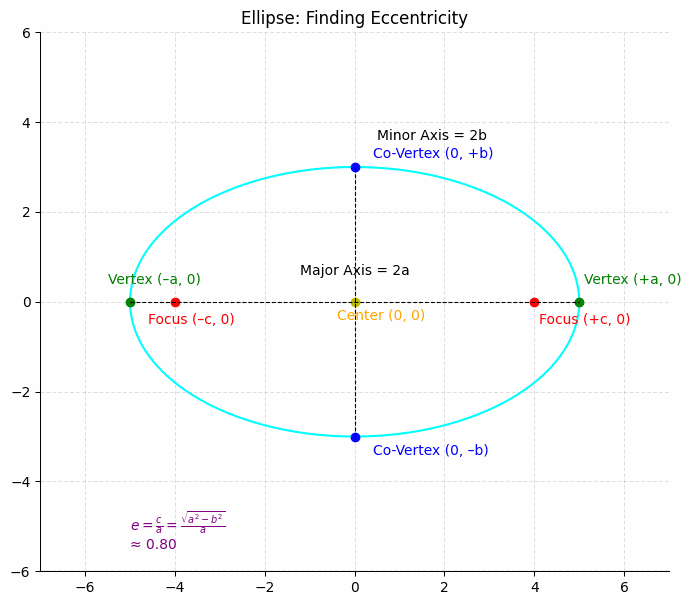
Solution:

a² = 25, so a = 5. b² = 9, so b = 3. We can find c using ##c^2 = a^2 – b^2##:

### c^2 = 25 – 9 ###### c = \sqrt{16} = 4 ###

Therefore, the eccentricity is:

### e = \frac{c}{a} = \frac{4}{5} = 0.8 ###

4. Applications Problems

These problems often involve applying the properties of ellipses to real-world scenarios. Carefully read the problem, identify the relevant information, and use the appropriate formulas and concepts to solve it.

Example 4:

An elliptical archway is 10 feet wide and 4 feet high at the center. Find the height of the archway 2 feet from the center.

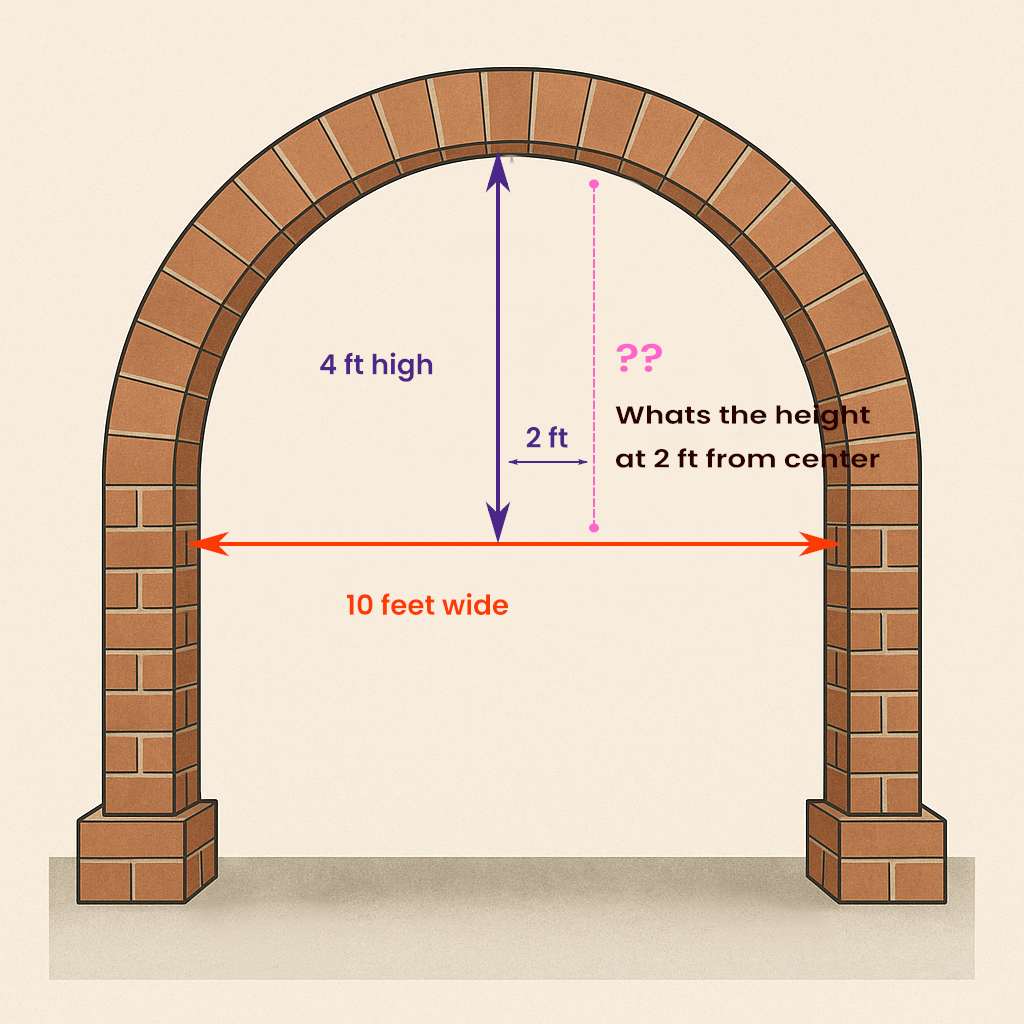
Solution:

We can model the archway as a semi-ellipse with the center at (0, 0). The width is 10 feet, so 2a = 10, and a = 5. The height is 4 feet, so b = 4.

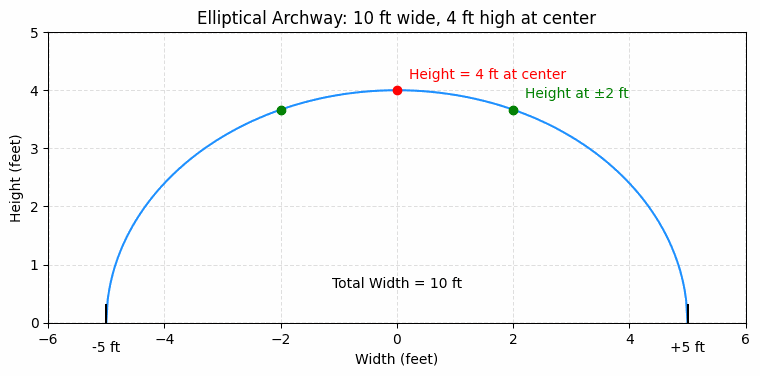
The equation of the ellipse is:

### \frac{x^2}{25} + \frac{y^2}{16} = 1 ###

We want to find the height (y-value) when x = 2 (2 feet from the center). Substitute x = 2 into the equation:

### \frac{2^2}{25} + \frac{y^2}{16} = 1 ###### \frac{4}{25} + \frac{y^2}{16} = 1 ###### \frac{y^2}{16} = 1 – \frac{4}{25} = \frac{21}{25} ###### y^2 = 16 \cdot \frac{21}{25} = \frac{336}{25} ###### y = \sqrt{\frac{336}{25}} \approx 3.66 ###

Therefore, the height of the archway 2 feet from the center is approximately 3.66 feet.

Summary and Further Exploration

In this lesson, we’ve covered the fundamental concepts of ellipses in coordinate geometry. We’ve explored their definition, properties, standard equations, graphing techniques, and real-world applications. Understanding ellipses is a crucial step in mastering conic sections and expanding your knowledge of geometry.

Here’s a summary of the key takeaways:

• An ellipse is defined by two foci and a constant sum of distances.
• The standard equations depend on the center and orientation of the ellipse.
• The values of a, b, and c are crucial for understanding the shape and properties of an ellipse.
• Ellipses have numerous applications in various fields.

To further your understanding, consider these additional topics:

• Parametric Equations of an Ellipse: Representing an ellipse using parametric equations.
• Tangents and Normals to an Ellipse: Finding the equations of tangent and normal lines.
• Applications in Calculus: Exploring the calculus of ellipses, such as finding areas and arc lengths.
• Other Conic Sections: Studying parabolas and hyperbolas.

Practice is key to mastering ellipses. Work through various problems, graph different ellipses, and explore their applications to solidify your understanding. Good luck, and enjoy the journey of learning!