Category theory, at its core, provides a powerful language for unifying diverse mathematical concepts. Category theory limits and colimits stand out as fundamental building blocks within this framework, offering a way to generalize and formalize a wide range of mathematical constructions. At its heart lie the concepts of limits and colimits, which provide a unified way to describe various constructions across different categories. These tools, essential for anyone aiming to grasp the abstract nature of modern mathematics, provide a lens through which we can view products, pullbacks, and much more.

---

---

Defining Limits: Universal Constructions in Action

The notion of a category theory limits provides a way to formalize the concept of a “universal construction.” It encapsulates the essential properties of familiar mathematical objects like products, pullbacks, and inverse limits. The definition of limits involves diagrams, cones, and a universal property that characterizes the “best possible” object satisfying certain conditions.

Diagrams and Cones: Setting the Stage

A diagram in a category C is a functor from an index category J to C. The index category J provides the shape or pattern for the diagram. A cone to a diagram F consists of an object N in C along with a family of morphisms from N to the objects in the diagram, satisfying a certain compatibility condition. This sets the groundwork for the formal definition of a limit.

The Universal Property: Identifying the Limit

The limit of a diagram is a cone, which is a “best possible” cone in the sense that any other cone to the same diagram must factor uniquely through it. This “universal property” is what makes limits so important. It ensures that the limit is uniquely determined up to a unique isomorphism, making it a well-defined and useful concept.

Examples of Limits: Products, Equalizers, and More

Familiar constructions such as products, equalizers, and pullbacks are all instances of limits. For example, the product of two objects is a limit of a diagram formed by those objects. The equalizer of two morphisms is a limit of a diagram involving those morphisms. Understanding these examples provides a concrete grasp of the abstract notion of a category theory limits.

Uniqueness and Existence: Exploring the Properties

If a diagram possesses a limit, that limit is unique up to isomorphism, which means that any two limits are essentially the same. However, not every diagram has a limit; the existence of limits depends on the specific category and the shape of the diagram. The study of limits encompasses both their existence and their properties.

Colimits: Duality and Dual Constructions

Colimits are the dual counterparts to limits. They capture the essence of constructions such as disjoint unions, direct sums, coproducts, pushouts, and direct limits. Understanding colimits involves reversing the direction of the morphisms and applying the same principles of diagrams, cones, and universal properties.

Cofibration

A cofibration is a map between topological spaces with a certain extension property. They play a crucial role in homotopy theory, forming the basis for constructing more complex spaces from simpler ones. This is very important.

Coproducts and Coequalizers: Examples of Colimits

Coproducts are examples of colimits, and they generalize the notion of disjoint unions. The coequalizer of two morphisms is also a colimit. Understanding these examples helps in grasping the abstract definition of colimits and their role in category theory. They are important to understand.

Pushouts: Constructing New Objects

Pushouts are another example of colimits, they are used to construct new objects from existing ones. Pushouts are especially important in algebraic topology. The construction can be visualized using commutative diagrams, and they offer a way to combine different objects in a consistent way.

Applications of Limits and Colimits: A Broader Perspective

The concepts of limits and colimits have far-reaching applications across various branches of mathematics and computer science. From algebraic topology to computer science, these constructions provide a common language for describing and relating different mathematical structures. The wide applicability of category theory limits highlights their fundamental importance.

Category Theory and Computer Science

In computer science, category theory, and specifically limits and colimits, finds applications in areas such as programming language semantics, type theory, and database theory. These concepts help in formalizing and understanding the structure of data and computation. The understanding is very useful.

Limits in Algebraic Topology

In algebraic topology, limits and colimits are fundamental tools for constructing and studying topological spaces. They are used in the construction of homotopy groups, homology, and cohomology theories, which are essential for classifying and understanding topological spaces. They help to understand complex spaces.

Limits in Functional Analysis

In functional analysis, limits and colimits are used to define and study various constructions, such as inverse limits of Banach spaces. This approach helps in analyzing and understanding the properties of operators and function spaces. These are critical in functional analysis.

Key Takeaways

Limits and colimits are fundamental concepts in category theory, providing a powerful framework for describing and relating mathematical structures. Understanding these concepts and their properties is essential for anyone seeking to understand the abstract nature of mathematics. These concepts provide a framework that unifies numerous mathematical constructions.

Similar Problems

1. Problem: Given a category C and a diagram F, find the product of two objects in C. Solution: The product is a limit of the diagram, described by a universal property with projections.

Product in a Category

In category theory, the product of two objects is a special type of construction that generalizes the Cartesian product of sets, the direct product of groups, and similar ideas in other mathematical structures.

Problem Statement

Problem: Given a category ##\mathcal{C}## and a diagram ##F## consisting of two objects, find the product of these objects in ##\mathcal{C}##.

Solution

The product of two objects ##A, B \in \mathcal{C}## is an object ##P## together with two projection morphisms ###\pi_A : P \to A, \quad \pi_B : P \to B,### such that for any other object ##X## with morphisms ###f : X \to A, \quad g : X \to B,### there exists a unique morphism ###u : X \to P###

This condition is called the universal property of the product. It ensures that the product is uniquely determined up to isomorphism.

Formal Definition

Formally, the product of objects ##A## and ##B## in a category ##\mathcal{C}## is the limit of the diagram:

A \longleftarrow \quad \cdot \quad \longrightarrow B

That is, the product is the object that represents the “best possible” way to map into both ##A## and ##B## simultaneously.

Examples

Category	Objects	Product
Set	Sets ##A, B##	Cartesian product ##A \times B##
Grp	Groups ##G, H##	Direct product of groups ##G \times H##
Top	Topological spaces ##X, Y##	Product topology on ##X \times Y##
Vectk	Vector spaces ##V, W##	Direct sum (same as direct product in finite case)

Additional Problem

Problem: In the category of groups, show that the product of two cyclic groups ##\mathbb{Z}_m## and ##\mathbb{Z}_n## is their direct product, and explain when this product is cyclic.

Solution:

The product in the category of groups is the direct product: ###\mathbb{Z}_m \times \mathbb{Z}_n.### This group is cyclic if and only if ##\gcd(m,n) = 1##, in which case ###\mathbb{Z}_m \times \mathbb{Z}_n \cong \mathbb{Z}_{mn}.### Otherwise, it is not cyclic.

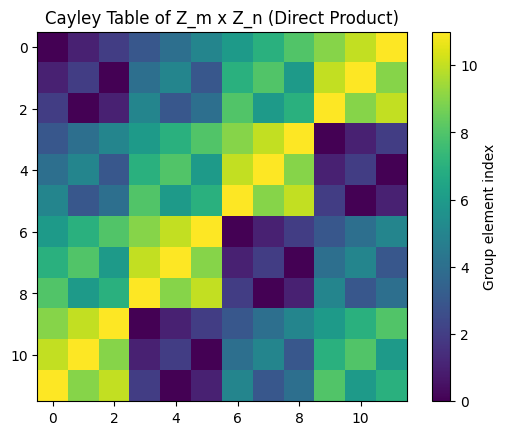
This heatmap illustrates how group elements combine under the direct product operation, helping us see structural properties such as cyclicity.

#Visualization with Python
#We can illustrate the direct product of two cyclic groups using a plot of their Cayley table.

import numpy as np
import matplotlib.pyplot as plt

# Parameters for cyclic groups Z_m and Z_n
m, n = 4, 3
G = [(i, j) for i in range(m) for j in range(n)]

# Cayley table of direct product Z_m x Z_n
table = np.zeros((len(G), len(G)), dtype=int)

for idx1, (a1, b1) in enumerate(G):
    for idx2, (a2, b2) in enumerate(G):
        prod = ((a1 + a2) % m, (b1 + b2) % n)
        table[idx1, idx2] = G.index(prod)

plt.imshow(table, cmap="viridis")
plt.colorbar(label="Group element index")
plt.title("Cayley Table of Z_m x Z_n (Direct Product)")
plt.show()

2. Problem: Given a category C and two morphisms f, g : A -> B, find the equalizer. Solution: The equalizer is a limit of the diagram defined by f and g, defined by a universal property.

Formal Expression

The equalizer can be seen as the limit of the diagram defined by the parallel pair ##f, g : A \to B##.

###E = \mathrm{Eq}(f,g) = \lim \left( A \rightrightarrows^{f}_{g} B \right)###

Thus, the equalizer is the most general solution to the condition “find morphisms into ##A## on which ##f## and ##g## act the same.”

Examples

Category	Equalizer
Sets	The subset of ##A## where ##f(a) = g(a)##, with inclusion map into ##A##.
Groups	The subgroup of ##A## consisting of elements mapped equally by ##f## and ##g##.
Vector Spaces	The kernel of ##f-g##, i.e., ##\{v \in A \mid f(v) = g(v)\}##.

Additional Problem

Consider two linear transformations on ##\mathbb{R}^2##:

f(x,y) = (x+y, y), \quad g(x,y) = (x, x+y)

Find the equalizer of ##f## and ##g## in the category of vector spaces.

Solution

We seek all vectors ##(x,y) \in \mathbb{R}^2## such that:

f(x,y) = g(x,y) \implies (x+y, y) = (x, x+y)

This gives the system of equations:

• ##x+y = x \implies y = 0##
• ##y = x+y \implies x = 0##

Thus the only solution is ##(0,0)##. Therefore, the equalizer is the zero subspace of ##\mathbb{R}^2##, with the trivial inclusion.

import numpy as np
import matplotlib.pyplot as plt

# Define f and g
def f(x, y):
    return np.array([x + y, y])

def g(x, y):
    return np.array([x, x + y])

# Generate grid points
X = np.linspace(-2, 2, 20)
Y = np.linspace(-2, 2, 20)
points = [(x, y) for x in X for y in Y]

# Check where f(x,y) = g(x,y)
equalizer_points = [(x, y) for x, y in points if np.allclose(f(x, y), g(x, y))]

# Plot
plt.axhline(0, color='black')
plt.axvline(0, color='black')
plt.scatter(*zip(*points), color='lightgray', s=10, label="All points")
if equalizer_points:
    plt.scatter(*zip(*equalizer_points), color='red', s=40, label="Equalizer points")

plt.title("Equalizer of f and g in R^2")
plt.legend()
plt.show()

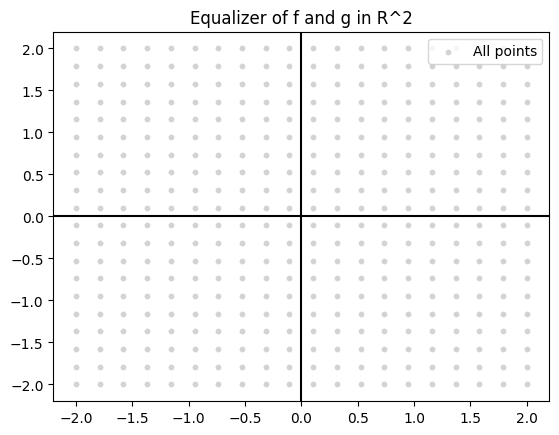
3. Problem: Explain the concept of a pullback in a category.

Solution: A pullback is a specific type of limit, defined by a universal property involving two morphisms with a common codomain.

4. Problem: Define a colimit and provide an example.

Solution: A colimit is the dual of a limit, such as a coproduct or a pushout, defined by a universal property.

5. Problem: How are limits and colimits used in computer science?

Solution: They are used in programming language semantics and type theory to model data structures and computation.

---

---