As θ → 0, we have cosθ → 1
Proof :
When θ = 0, We have, lim\(_{θ\to 0} \cos \)θ = cos0 = 1 { ∵ cos0 = 1 }
Hence,
ADVERTISEMENT

As θ → 0, we have cosθ → 1
Proof :
When θ = 0, We have, lim\(_{θ\to 0} \cos \)θ = cos0 = 1 { ∵ cos0 = 1 }
Hence,

OpenAI’s open-weight models offer new ways to assess AI models, especially for secure operations. Learn how this shift impacts the military and other sensitive sectors.

The Shenzhou-21 mission successfully returned to Earth, setting a new record for the longest time in space for Chinese astronauts. The mission allows us to **explore space missions** and the future of space exploration.

INTRODUCTION: WHAT IS DYNAMICS? Dynamics is the part of mechanics that studies how forces affect the motion of...
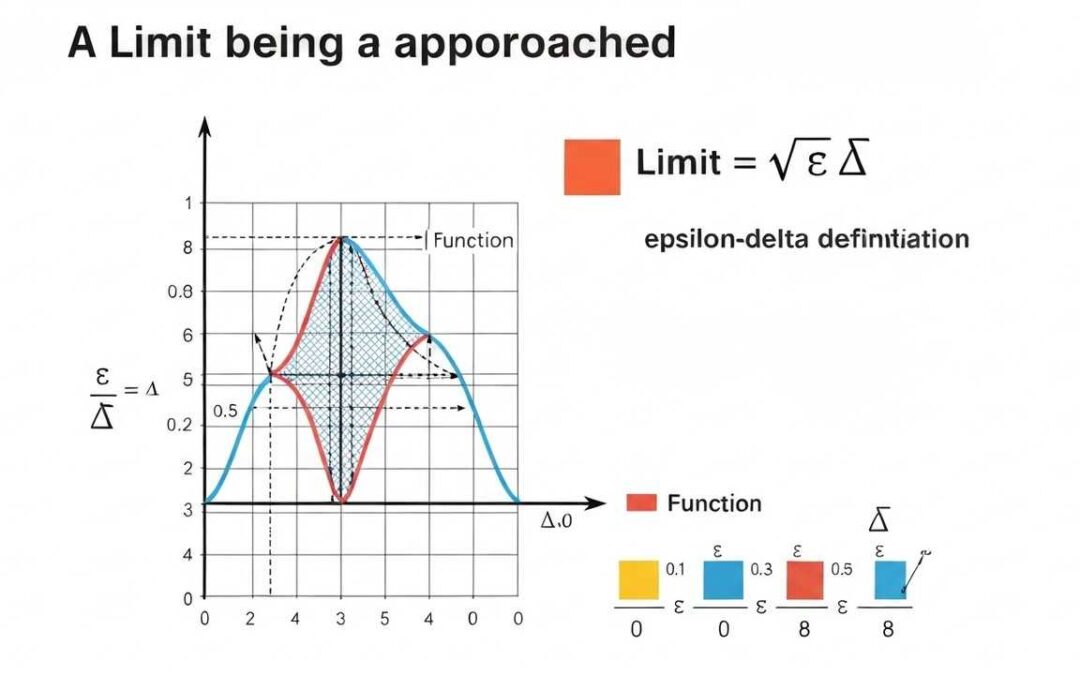
Understanding **limits of functions** is essential in calculus. This guide explains the epsilon-delta definition, theorems, and applications to help you master this fundamental concept.
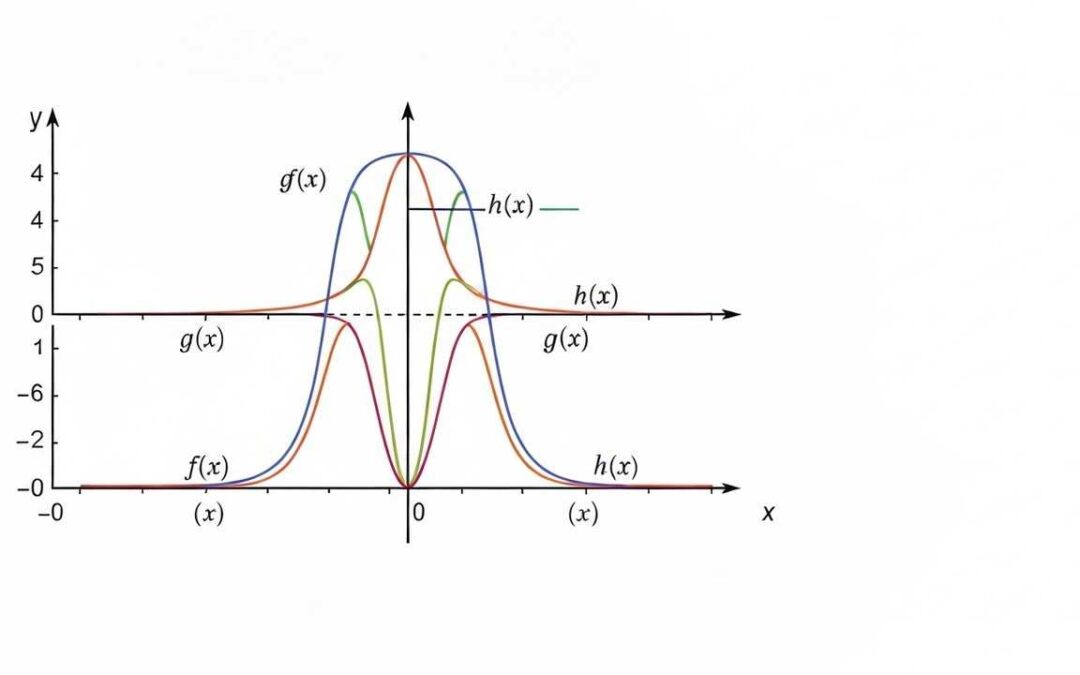
The Squeeze Theorem is a calculus concept that uses bounding functions to determine the limit of a function. The article explains how it works and provides examples.
Learn how to solve Evaluating Limits Problems with this step-by-step guide. We’ll cover the fundamentals and provide clear examples.

Learn how to solve Limits at Infinity with this comprehensive guide. Understand the concepts and techniques through clear examples and step-by-step solutions.
0 Comments