Carnot efficiency calculation is fundamental for understanding the maximum potential of heat engines. This concept, based on the Carnot cycle, provides a theoretical limit on the efficiency of converting heat into work. You’ll learn to master Carnot efficiency calculation and understand its implications in real-world applications, from power plants to internal combustion engines.
Table of Contents
- Understanding the Essence of Carnot Efficiency
- The Core Principles of the Carnot Cycle
- The Four Reversible Processes (at a Glance)
- Why Carnot Efficiency Matters
- Worked Numbers & Quick Comparisons
- Visualizing How Temperatures Shape Efficiency
- Practical Implications
- How Temperature Differences Affect Efficiency
- Two Illustrative Cases
- Trend with Hot-Reservoir Temperature (##T_\text{cold}=300\ \text{K}##)
- Lowering the Cold-Reservoir Temperature
- Practical Limits
- Exploring Real-World Challenges
- Numerical Problems
- Carnot Efficiency Problem Set — Worked Solutions, Tables, and Plot
- Key Takeaways
Read More
Today, we will focus on the concept of Carnot efficiency calculation, a cornerstone in understanding how efficiently these engines can convert thermal energy into mechanical work. This exploration is crucial for mechanical engineering students, physicists, and anyone keen on grasping the theoretical boundaries of energy conversion. Let’s embark on this journey to uncover the secrets of ideal heat engine performance.
Understanding the Essence of Carnot Efficiency
The Carnot cycle—conceived by Sadi Carnot—defines the theoretical ceiling on the efficiency of any heat engine operating between two thermal reservoirs. It consists of four reversible processes: isothermal expansion, adiabatic expansion, isothermal compression, and adiabatic compression. Because all steps are reversible, the cycle sets a benchmark: no real engine can surpass its efficiency, and real machines fall short due to irreversibilities such as friction, finite-temperature heat transfer, fluid turbulence, and heat leaks.
The Core Principles of the Carnot Cycle
A Carnot engine operates between a hot reservoir at temperature ##T_\text{hot}## and a cold reservoir at temperature ##T_\text{cold}## (both in Kelvin). For any reversible engine, the efficiency depends only on these absolute temperatures—independent of the working substance or mechanical details. Running the sequence in reverse yields the reversed Carnot cycle, which functions as an ideal refrigerator or heat pump.
The maximum (Carnot) efficiency for a heat engine is
###\eta_\text{Carnot} \;=\; 1 \;-\; \dfrac{T_\text{cold}}{T_\text{hot}}###
Because Kelvin temperatures are strictly positive, the expression makes key limits transparent: efficiency grows when ##T_\text{hot}## increases or ##T_\text{cold}## decreases; perfect efficiency (##\eta=1##) would require ##T_\text{cold}=0\ \text{K}##, which is unattainable by the third law. Thus, Carnot efficiency is an ideal upper bound dictated by the second law.
The Four Reversible Processes (at a Glance)
| Stage | Process Type | Thermal Contact | Qualitative Effect |
|---|---|---|---|
| 1 → 2 | Isothermal Expansion | At ##T_\text{hot}## | Absorbs heat ##Q_\text{in}## while doing work; temperature constant |
| 2 → 3 | Adiabatic Expansion | Thermally isolated | Does work; internal energy drops; temperature falls to ##T_\text{cold}## |
| 3 → 4 | Isothermal Compression | At ##T_\text{cold}## | Rejects heat ##Q_\text{out}## to the cold reservoir; temperature constant |
| 4 → 1 | Adiabatic Compression | Thermally isolated | Work is done on the gas; temperature rises back to ##T_\text{hot}## |
Why Carnot Efficiency Matters
- Upper bound: It caps the performance of all conceivable engines between ##T_\text{hot}## and ##T_\text{cold}##
- Design target: Guides materials, combustion, and heat-exchanger design toward wider temperature spans and reduced losses.
- Universality: Independent of working fluid and mechanism—steam, gas-turbine, Stirling, or Brayton cycles all obey the same limit.
Worked Numbers & Quick Comparisons
| Case | ##T_\text{hot}## (K) | ##T_\text{cold}## (K) | ###\eta_\text{Carnot} = 1 – T_c/T_h### | Interpretation |
|---|---|---|---|---|
| Industrial Boiler + Ambient | ##800## | ##300## | ###1 – \tfrac{300}{800} = 0.625### | Max 62.5% even with ideal reversibility |
| High-Temp Gas Turbine + Ambient | ##1500## | ##300## | ###1 – \tfrac{300}{1500} = 0.80### | 80% ceiling; real cycles are much lower |
| Waste-Heat Recovery | ##500## | ##320## | ###1 – \tfrac{320}{500} = 0.36### | Small temperature span restricts the limit |
Visualizing How Temperatures Shape Efficiency
Below are two simple charts illustrating how Carnot efficiency varies with reservoir temperatures. The first varies ##T_\text{cold}## at fixed ##T_\text{hot}##; the second varies ##T_\text{hot}## at fixed ##T_\text{cold}##.
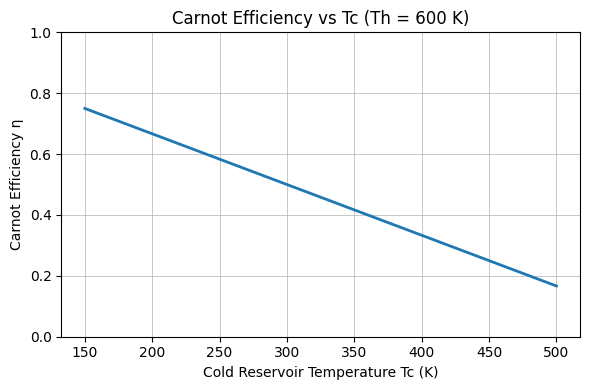
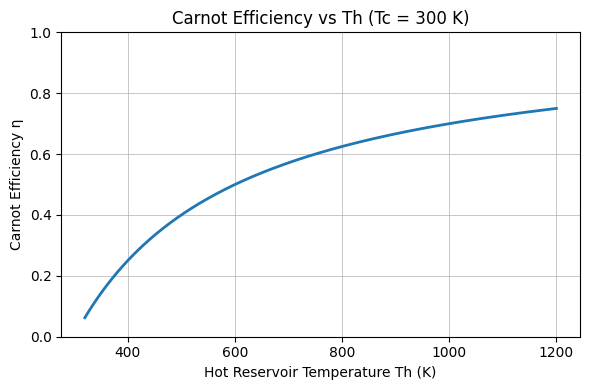
Practical Implications
The implications of the Carnot efficiency are profound, shaping the design and operation of various heat engines. From internal combustion engines in cars to power plants generating electricity, the principles of the Carnot cycle are at play. Understanding these principles allows engineers to optimize designs for maximum efficiency, considering factors like material limitations and operational costs. Furthermore, it underscores the importance of waste heat recovery in industrial processes.
How Temperature Differences Affect Efficiency
The Carnot efficiency gives the theoretical upper bound for any heat engine operating between two reservoirs at absolute temperatures ##T_\text{hot}## and ##T_\text{cold}##:
###\eta_\text{Carnot} = 1 – \dfrac{T_\text{cold}}{T_\text{hot}}###
Because only temperatures appear, widening the temperature gap (raising ##T_\text{hot}## or lowering ##T_\text{cold}##) is the only way—ideally—to increase the maximum possible efficiency. Real engines will always be less efficient due to irreversibilities, but Carnot provides a clean benchmark.
Two Illustrative Cases
| Case | ##T_\text{hot}## (K) | ##T_\text{cold}## (K) | Computation | ###\eta_\text{Carnot}### | Comment |
|---|---|---|---|---|---|
| A | ##600## | ##300## | ###1 – \tfrac{300}{600}### | ###0.50 \;(50\%)### | Half of the input heat can be converted to work in the ideal limit. |
| B | ##1000## | ##300## | ###1 – \tfrac{300}{1000}### | ###0.70 \;(70\%)### | Raising ##T_\text{hot}## increases the ideal ceiling—but materials and safety limit how high we can go. |
Trend with Hot-Reservoir Temperature (##T_\text{cold}=300\ \text{K}##)
The curve below shows how ###\eta_\text{Carnot} = 1 – \dfrac{300}{T_\text{hot}}### grows as ##T_\text{hot}## rises, with markers at the two example points. Note the diminishing returns: each additional Kelvin at high temperatures yields smaller efficiency gains.
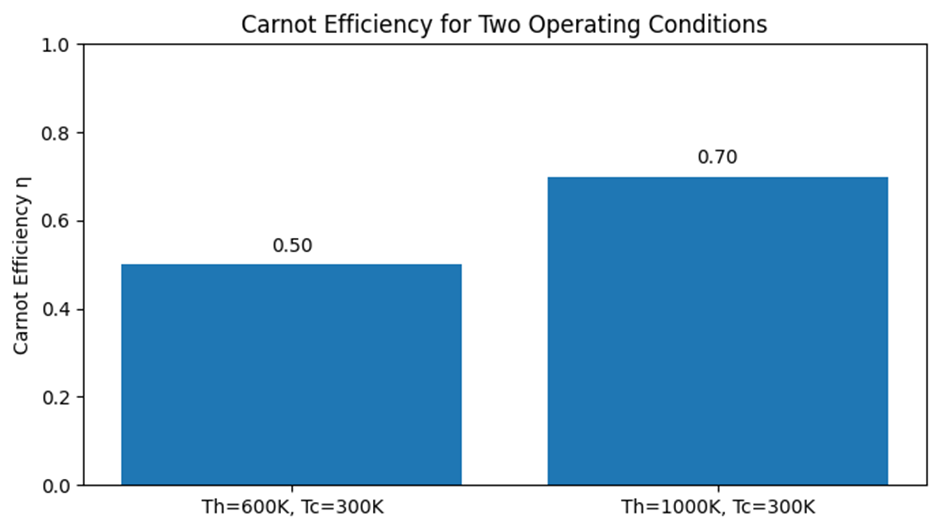
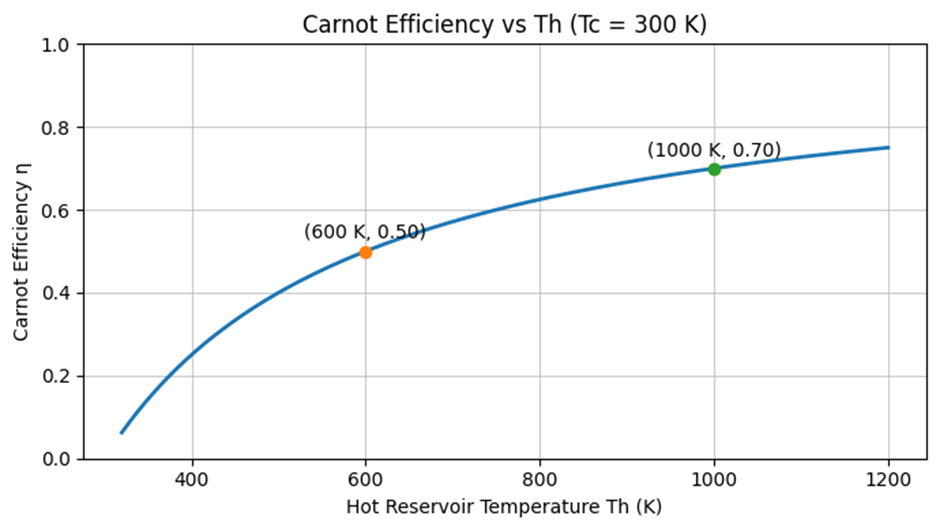
Lowering the Cold-Reservoir Temperature
Because ###\eta_\text{Carnot} = 1 – \dfrac{T_\text{cold}}{T_\text{hot}}###, reducing ##T_\text{cold}## likewise boosts the ideal efficiency. This motivates advanced condensers, improved heat rejection, and access to cooler sinks (e.g., evaporative cooling or ocean-water intake). In practice, environmental constraints, water availability, and exchanger sizing limit how low ##T_\text{cold}## can go.
Practical Limits
- Materials & safety: Turbine blades, boiler tubes, and combustor linings govern the maximum sustainable ##T_\text{hot}##.
- Irreversibilities: Friction, finite-rate heat transfer, and leakage ensure real efficiencies fall below the Carnot line.
- Design focus: Widen the temperature span where feasible, while minimizing losses to approach the Carnot benchmark.
Exploring Real-World Challenges
While the Carnot cycle provides a theoretical ideal, real-world engines face numerous challenges. Friction, heat losses to the environment, and incomplete combustion are among the factors that reduce engine efficiency. Furthermore, the design of heat exchangers, turbines, and other components introduces additional inefficiencies. Overcoming these challenges is crucial for improving engine performance and reducing energy waste.
Overcoming Practical Limitations
Engineers employ various strategies to minimize these losses. Improving materials, optimizing combustion processes, and enhancing heat exchange designs are common approaches. Waste heat recovery systems, which capture and reuse exhaust heat, are another promising avenue. These efforts aim to bring the engine’s performance closer to the theoretical Carnot limit. These strategies are essential when attempting to perform a Carnot efficiency calculation.
The Carnot cycle helps to understand the maximum potential of any heat engine. It serves as a target for engineers striving to improve engine efficiency. Even though the ideal conditions of the Carnot cycle are impossible to achieve in practice, understanding its principles helps engineers to design engines more efficiently. The principles of the Carnot cycle are widely used in the field of Carnot efficiency calculation.
Technological advancements, such as improved materials and advanced combustion techniques, are continuously pushing the boundaries of engine performance. However, the Carnot limit remains a fundamental constraint. Even with these advances, it is critical to acknowledge the second law of thermodynamics. Therefore, the main goal is to get closer to the theoretical efficiency limit.
Numerical Problems
Problem 1
Calculate the Carnot efficiency of a heat engine operating between 800 K and 400 K.
Problem 2
A heat engine operates with a hot reservoir at 1200 K and a cold reservoir at 300 K. What is its maximum theoretical efficiency?
Problem 3
If a Carnot engine’s cold reservoir is at 20°C (293 K) and its efficiency is 60%, what is the hot reservoir’s temperature?
Problem 4
Determine the Carnot efficiency if ##T_hot## is doubled and ##T_cold## remains the same.
Problem 5
A heat engine has a Carnot efficiency of 40% with ##T_cold = 250 K##. What is ##T_hot##?
Carnot Efficiency Problem Set — Worked Solutions, Tables, and Plot
We use the Carnot formula (temperatures in Kelvin):
###\eta_\text{Carnot} \;=\; 1 – \dfrac{T_\text{cold}}{T_\text{hot}}###
Problem 1
Prompt. Calculate the Carnot efficiency of a heat engine operating between 800 K and 400 K.
Solution. ###\eta = 1 – \tfrac{400}{800} = 1 – 0.5 = 0.5 = 50\%###
Answer. 50%
Problem 2
Prompt. A heat engine operates with a hot reservoir at 1200 K and a cold reservoir at 300 K. What is its maximum theoretical efficiency?
Solution. ###\eta = 1 – \tfrac{300}{1200} = 1 – 0.25 = 0.75 = 75\%###
Answer. 75%
Problem 3
Prompt. If a Carnot engine’s cold reservoir is at 20°C (293 K) and its efficiency is 60%, what is the hot reservoir’s temperature?
Solution. From ###\eta = 1 – \tfrac{T_c}{T_h}###, we get ###T_h = \tfrac{T_c}{1-\eta} = \tfrac{293}{0.4} = 732.5\ \text{K}###.
Answer. 732.5 K
Problem 4
Prompt. Determine the Carnot efficiency if ##T_\text{hot}## is doubled and ##T_\text{cold}## remains the same.
General Result. Let the original efficiency be ###\eta_1 = 1 – \tfrac{T_c}{T_h}###. After doubling ##T_h## to ##2T_h##, the new efficiency is
###\eta_2 = 1 – \dfrac{T_c}{2T_h} = 1 – \dfrac{1}{2}\Big(\dfrac{T_c}{T_h}\Big) = 1 – \dfrac{1}{2}(1-\eta_1) = \dfrac{1}{2} + \dfrac{\eta_1}{2}.###
Since ###0 \le (1-\eta_1) \le 1###, we have ###\eta_2 > \eta_1### (unless ##\eta_1=1## which is impossible). Thus, efficiency increases, specifically to the average of 100% and the old efficiency.
Answer. Efficiency increases (quantitatively, ###\eta_2=\tfrac{1}{2}(1+\eta_1)###).
Problem 5
Prompt. A heat engine has a Carnot efficiency of 40% with ##T_\text{cold}=250\ \text{K}##. What is ##T_\text{hot}##?
Solution. ###\eta = 0.40 = 1 – \tfrac{250}{T_h}\ \Rightarrow\ \tfrac{250}{T_h}=0.60\ \Rightarrow\ T_h=\tfrac{250}{0.60}=416.67\ \text{K}###.
Answer. 416.67 K
Summary Table
| Problem | ##T_\text{hot}## (K) | ##T_\text{cold}## (K) | Given/Target | Computation | Result |
|---|---|---|---|---|---|
| P1 | 800 | 400 | Find ##\eta## | ###1-\tfrac{400}{800}### | ###0.50 \;(50\%)### |
| P2 | 1200 | 300 | Find ##\eta## | ###1-\tfrac{300}{1200}### | ###0.75 \;(75\%)### |
| P3 | ##T_h=?## | 293 | Given ##\eta=0.60## | ###T_h=\tfrac{293}{1-0.60}### | ###732.5\ \text{K}### |
| P4 | ##2T_h## | ##T_c## | Compare with old ##\eta_1## | ###\eta_2=\tfrac{1}{2}(1+\eta_1)### | Increases |
| P5 | ##T_h=?## | 250 | Given ##\eta=0.40## | ###T_h=\tfrac{250}{1-0.40}### | ###416.67\ \text{K}### |
Key Takeaways
In conclusion, the Carnot efficiency calculation provides a critical framework for understanding the limits of heat engine performance. The Carnot cycle serves as a benchmark, highlighting the importance of temperature differences in maximizing efficiency. While real-world engines face practical challenges, the pursuit of improved efficiency remains a central goal in engineering. By understanding the theoretical limits imposed by the Carnot cycle, engineers can make informed decisions and design more efficient and sustainable energy systems. Therefore, Carnot efficiency calculation is a pivotal topic in thermodynamics.
| Parameter | Description | Formula |
|---|---|---|
| Carnot Efficiency (η) | The maximum theoretical efficiency of a heat engine. | ##η_Carnot = 1 – T_cold / T_hot## |
| Hot Reservoir Temperature (##T_hot##) | The temperature of the hot reservoir in Kelvin (K). | Measured in Kelvin (K) |
| Cold Reservoir Temperature (##T_cold##) | The temperature of the cold reservoir in Kelvin (K). | Measured in Kelvin (K) |
| Efficiency Limitations | Real-world engines cannot reach 100% efficiency due to the second law of thermodynamics. | Always less than the theoretical Carnot efficiency. |
We also Published
RESOURCES
- Carnot Efficiency Calculator
- The Carnot Efficiency | EGEE 102: Energy Conservation and …
- Carnot cycle – Wikipedia
- Carnot Cycle
- Why do PWR reactors have very low Carnot Efficiency? : r/nuclear
- Carnot Efficiency – an overview | ScienceDirect Topics
- Efficiency of a Carnot engine
- Carnot efficiency – Energy Education
- Carnot Efficiency Calculator
- 4.6: The Carnot Cycle – Physics LibreTexts



0 Comments