Estimated reading time: 10 minutes
Heat conduction rate calculation is a fundamental concept in physics and engineering, essential for understanding how thermal energy moves through materials. It governs a wide array of applications, from designing energy-efficient buildings to optimizing electronic device cooling systems. Mastering this principle provides a strong foundation for tackling complex thermal challenges.
This crucial understanding allows engineers to predict and control heat transfer, vital for thermal management in everything from spacecraft design to everyday electronics. By accurately calculating heat flow, it enables the creation of more efficient and durable products while minimizing energy waste.
Table of Contents
- What is Heat Conduction?
- Understanding Thermal Energy Transfer
- Modes of Heat Transfer
- Heat Conduction Equation
- Factors Influencing Heat Transfer
- Thermal Conductivity of Common Materials
- Example Problem
- Fourier’s Law of Heat Conduction
- Mathematical Formulation
- Physical Meaning
- Example Problem
- Quick Reference Table
- Heat Conduction Rate Calculation: A Practical Example
- Numerical Problems
- Solved Problems Using Fourier’s Law of Heat Conduction
- Problem 1: Heat Loss Through a Wall
- Problem 2: Heat Transfer Through Copper Rod
- Problem 3: Heat Loss Through an Insulated Pipe
- Problem 4: Heat Transfer Through Refrigerator Wall
- Problem 5: Heat Loss Through Fiberglass Insulation
- Key Takeaways
Read More
Understanding how heat transfers through materials is critical for engineers and physicists alike. This guide will help you to heat conduction rate calculation, enabling you to analyze thermal properties and design efficient insulation systems. From the fundamentals of Fourier’s Law to practical problem-solving, we explore the core principles that govern heat transfer.
What is Heat Conduction?
Heat conduction is the process by which thermal energy is transferred from a region of higher temperature to a region of lower temperature within a solid, liquid, or gas, primarily through direct contact. This transfer occurs at the molecular level, where more energetic particles collide with less energetic ones, sharing their kinetic energy without any macroscopic movement of the material itself. The efficiency of heat conduction depends heavily on the material’s properties, most notably its thermal conductivity, which quantifies how readily a material conducts heat.
In solids, heat conduction is primarily facilitated by the vibrations of atoms in a lattice and the movement of free electrons, particularly in metals. In liquids and gases, molecular collisions are the dominant mechanism. Understanding this process is crucial for various applications, from designing effective insulation to engineering efficient heat sinks for electronic components.
Understanding Thermal Energy Transfer
Thermal energy transfer is a cornerstone concept in thermodynamics, describing how heat flows from regions of higher temperature to regions of lower temperature. This transfer occurs due to temperature differences and is shaped by the physical properties of the materials involved. It underpins diverse applications ranging from household insulation and cooking utensils to large-scale engineering systems such as power plants and spacecraft.
Heat conduction is a key mechanism for heat transfer in solids, where molecules are closely packed and can easily transfer energy through collisions. Metals, for example, are excellent conductors due to the presence of free electrons that facilitate rapid energy transfer. Conversely, insulators like wood or plastic resist heat flow because their molecular structure hinders energy transfer.
The rate of thermal energy transfer is influenced by several factors. These include the temperature difference between the two regions, the material’s thermal conductivity, the area through which heat is transferred, and the thickness of the material. Understanding these factors is crucial for predicting and controlling heat flow in various applications.
Modes of Heat Transfer
There are three primary mechanisms of thermal energy transfer:
- Conduction: Occurs mainly in solids, where heat passes through molecular vibrations and collisions. Metals are excellent conductors due to the mobility of free electrons that carry energy quickly. Insulators like wood, rubber, or plastic resist this flow because of their tightly bound electrons.
- Convection: Dominates in fluids (liquids and gases). Heat transfer happens as warmer, less dense fluid rises and cooler, denser fluid sinks, creating convection currents. This is the principle behind boiling water and atmospheric circulation.
- Radiation: Transfer of energy through electromagnetic waves, requiring no medium. The Sun’s heat reaches Earth via radiation across the vacuum of space.
Heat Conduction Equation
For steady-state one-dimensional conduction, Fourier’s law gives the rate of heat transfer:
### Q = \frac{k \, A \, \Delta T}{d} ###
- Q = rate of heat transfer (W)
- k = thermal conductivity of material (W/m·K)
- A = cross-sectional area (m²)
- ΔT = temperature difference (K or °C)
- d = thickness of material (m)
Factors Influencing Heat Transfer
Several parameters control how effectively heat is transferred:
- Temperature difference: Greater temperature gradients increase the rate of heat flow.
- Material conductivity: Metals like copper and aluminum conduct heat efficiently, while insulators like glass wool and polystyrene reduce heat transfer.
- Surface area: Larger areas allow more heat to flow across.
- Thickness of material: Thicker barriers slow down heat transfer.
Thermal Conductivity of Common Materials
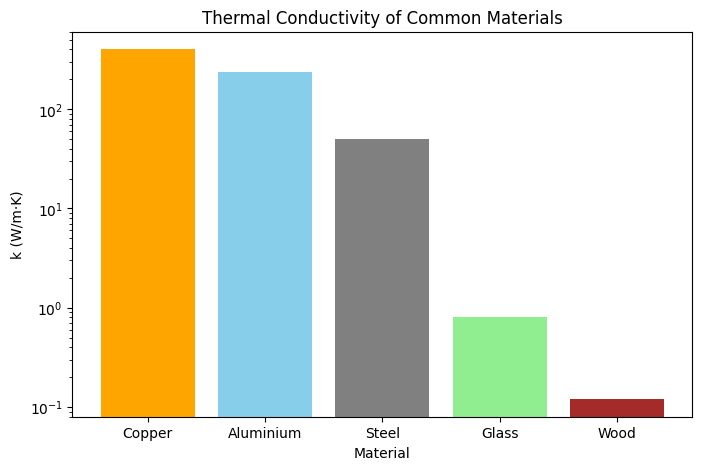
| Material | Thermal Conductivity k (W/m·K) | Remarks |
|---|---|---|
| Copper | 401 | Excellent conductor, used in wiring & cookware |
| Aluminium | 237 | Lightweight conductor, used in heat exchangers |
| Steel | 50 | Moderate conductor, used in structures |
| Glass | 0.8 | Poor conductor, good insulator in windows |
| Wood | 0.12 | Very poor conductor, natural insulator |
Example Problem
Problem: A copper plate 0.01 m thick and 0.5 m² in area separates two environments with a temperature difference of 50°C. Find the rate of heat transfer (k = 401 W/m·K).
Solution:
### Q = \frac{k \, A \, \Delta T}{d} = \frac{401 \cdot 0.5 \cdot 50}{0.01} = 1.00 \times 10^6 \,\text{W} ###
Answer: The heat transfer rate is 1 MW, showing why copper is widely used where rapid heat conduction is required.
Fourier’s Law of Heat Conduction
Fourier’s Law, a cornerstone of heat transfer, mathematically describes the rate at which heat flows through a material. It states that the heat transfer rate is proportional to the area of the material, the temperature gradient (the change in temperature over distance), and the material’s thermal conductivity. This law is essential for quantifying heat transfer in engineering and physics.
Mathematical Formulation
The law is expressed as:
### \dfrac{Q}{\Delta t} = -k A \dfrac{\Delta T}{\Delta x} ###
- Q/Δt → Rate of heat transfer (W, or J/s)
- k → Thermal conductivity of the material (W/m·°C)
- A → Cross-sectional area perpendicular to heat flow (m²)
- ΔT → Temperature difference (°C)
- Δx → Thickness of material (m)
The negative sign signifies that heat always flows from regions of higher temperature to regions of lower temperature, i.e., in the direction opposite to the temperature gradient.
Physical Meaning
- High k (thermal conductivity) means the material transfers heat rapidly (e.g., copper, aluminum).
- Larger A allows more heat to flow.
- Greater ΔT drives faster transfer.
- Thicker material (Δx) reduces the rate of heat flow.
This equation is fundamental for understanding and calculating heat transfer rates in various scenarios, from designing building insulation to analyzing heat sinks in electronics. By understanding the components of Fourier’s Law, engineers can predict how much heat will flow through a material under specific conditions and design systems to manage thermal energy effectively.
Example Problem
Problem: A wall 0.2 m thick has an area of 10 m². The inside surface is at 25°C and the outside surface at 5°C. The material’s thermal conductivity is 0.8 W/m·°C. Find the heat transfer rate.
Solution:
### \dfrac{Q}{\Delta t} = \dfrac{k A \Delta T}{\Delta x} = \dfrac{(0.8)(10)(25 – 5)}{0.2} ###
### \dfrac{Q}{\Delta t} = \dfrac{0.8 \times 10 \times 20}{0.2} = \dfrac{160}{0.2} = 800 \,\text{W} ###
Answer: The wall transfers 800 W of heat.
Quick Reference Table
| Parameter | Symbol | Units | Role in Heat Transfer |
|---|---|---|---|
| Thermal Conductivity | k | W/m·°C | Higher k → faster conduction |
| Cross-sectional Area | A | m² | Larger A → greater heat transfer |
| Temperature Difference | ΔT | °C or K | Greater ΔT → more driving force |
| Material Thickness | Δx | m | Greater Δx → less conduction |
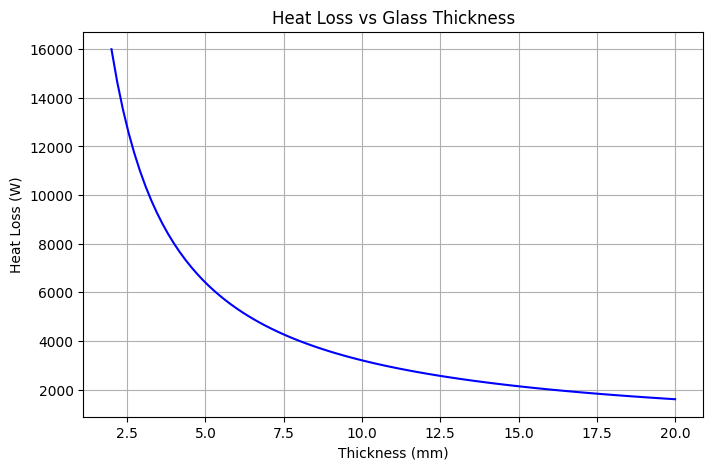
Heat Conduction Rate Calculation: A Practical Example
Let’s calculate the rate of heat loss through a windowpane using Fourier’s Law. This example illustrates how material properties and temperature differences affect heat transfer. We will solve a specific problem to show how to apply the formula and understand the results.
This example demonstrates how to apply Fourier’s Law of Heat Conduction to a real-world case: calculating heat loss through a glass windowpane. Such calculations are essential in building physics and energy conservation, as they highlight how much energy escapes through poorly insulated surfaces.
Problem Setup
- Width of window: 1 m
- Height of window: 2 m
- Area (A): 1 × 2 = 2 m²
- Thickness (Δx): 0.005 m
- Thermal conductivity of glass (k): 0.8 W/m·°C
- Inside temperature: 20°C
- Outside temperature: 0°C
- Temperature difference (ΔT): 20°C
Applying Fourier’s Law
The formula for steady-state conduction is:
### \dfrac{Q}{\Delta t} = -k A \dfrac{\Delta T}{\Delta x} ###
Substitute known values:
### \dfrac{Q}{\Delta t} = -(0.8)(2)\dfrac{20}{0.005} ###
### \dfrac{Q}{\Delta t} = -0.8 \times 2 \times 4000 ###
### \dfrac{Q}{\Delta t} = -6400 \,\text{W} ###
Final Answer
The windowpane transfers 6400 W of heat (negative sign indicating heat flows outward). This means 6.4 kW of energy is lost every second through a single pane of glass under these conditions.
Insight
This result demonstrates the poor insulating ability of ordinary glass. Significant heat loss occurs because of its relatively high conductivity and thin thickness. To reduce this energy loss, buildings often use:
- Double or triple glazing (increasing effective thickness and air gaps)
- Low-emissivity (Low-E) coatings to reduce radiation losses
- Materials with lower conductivity (e.g., specialized insulated glass units)
Numerical Problems
1. Calculate the heat loss through a wall (area = 10 m², thickness = 0.1 m, k = 0.1 W/m°C, ΔT = 15°C).
2. Determine the heat transfer rate through a copper rod (area = 0.01 m², length = 0.5 m, k = 400 W/m°C, ΔT = 50°C).
3. Find the heat loss through an insulated pipe (area = 0.5 m², thickness = 0.02 m, k = 0.05 W/m°C, ΔT = 30°C).
4. Compute the heat transfer rate through a refrigerator wall (area = 2 m², thickness = 0.03 m, k = 0.03 W/m°C, ΔT = 25°C).
5. Calculate the heat loss through a fiberglass insulation layer (area = 5 m², thickness = 0.15 m, k = 0.04 W/m°C, ΔT = 20°C).
Solved Problems Using Fourier’s Law of Heat Conduction
We apply Fourier’s Law in steady-state, one-dimensional conduction:
### \dfrac{Q}{\Delta t} = \dfrac{k A \Delta T}{\Delta x} ###
- Q/Δt = Heat transfer rate (W)
- k = Thermal conductivity (W/m°C)
- A = Area (m²)
- ΔT = Temperature difference (°C)
- Δx = Thickness/length of the material (m)
Problem 1: Heat Loss Through a Wall
Given: A = 10 m², Δx = 0.1 m, k = 0.1 W/m°C, ΔT = 15°C.
### Q/Δt = \dfrac{(0.1)(10)(15)}{0.1} = \dfrac{15}{0.1} = 150 \,\text{W} ###
Answer: Heat loss = 150 W.
Problem 2: Heat Transfer Through Copper Rod
Given: A = 0.01 m², Δx = 0.5 m, k = 400 W/m°C, ΔT = 50°C.
### Q/Δt = \dfrac{(400)(0.01)(50)}{0.5} = \dfrac{200}{0.5} = 400 \,\text{W} ###
Answer: Heat transfer rate = 400 W.
Problem 3: Heat Loss Through an Insulated Pipe
Given: A = 0.5 m², Δx = 0.02 m, k = 0.05 W/m°C, ΔT = 30°C.
### Q/Δt = \dfrac{(0.05)(0.5)(30)}{0.02} = \dfrac{0.75}{0.02} = 37.5 \,\text{W} ###
Answer: Heat loss = 37.5 W.
Problem 4: Heat Transfer Through Refrigerator Wall
Given: A = 2 m², Δx = 0.03 m, k = 0.03 W/m°C, ΔT = 25°C.
### Q/Δt = \dfrac{(0.03)(2)(25)}{0.03} = \dfrac{1.5}{0.03} = 50 \,\text{W} ###
Answer: Heat transfer rate = 50 W.
Problem 5: Heat Loss Through Fiberglass Insulation
Given: A = 5 m², Δx = 0.15 m, k = 0.04 W/m°C, ΔT = 20°C.
### Q/Δt = \dfrac{(0.04)(5)(20)}{0.15} = \dfrac{4}{0.15} \approx 26.67 \,\text{W} ###
Answer: Heat loss ≈ 26.7 W.
Key Takeaways
Understanding heat conduction rate calculation is crucial for anyone studying physics or engineering. By mastering Fourier’s Law and its applications, you can analyze and solve a wide range of thermal problems. The ability to determine heat transfer rates allows for better designs and more efficient use of energy.
Remember that thermal conductivity, material thickness, and temperature differences significantly impact heat transfer. This knowledge is essential for designing effective insulation, heat sinks, and other thermal management systems. Through the examples provided, you can apply this knowledge to solve real-world problems.
| Parameter | Symbol | Units | Description |
|---|---|---|---|
| Rate of Heat Transfer | Q/Δt | Watts (W) | The amount of heat energy transferred per unit of time. |
| Thermal Conductivity | k | W/m°C | A material’s ability to conduct heat. High k = good conductor. |
| Area | A | Square meters (m²) | The surface area through which heat is transferred. |
| Temperature Difference | ΔT | °C | The difference in temperature between two points. |
| Thickness | Δx | Meters (m) | The distance through which heat is transferred. |
We also Published
RESOURCES
- Heat Transfer Conduction Calculator | Thermtest Inc.
- Rate of heat flow – Wikipedia
- Conduction | Physics
- Heat Transfer | Equation, Formula & Rate – Lesson | Study.com
- Thermal conduction – Wikipedia
- Conductive Heat Transfer
- Staedy Conduction Heat Transfer.pdf
- Conduction Heat Transfer | Engineering Library
- Image based heating rate calculation from thermographic data …
- HEAT TRANSFER EQUATION SHEET



0 Comments