Calculating specific heat capacity is crucial for understanding how materials respond to heat. This guide provides a comprehensive overview of specific heat capacity, including its definition, formula, and practical applications. You’ll learn how to calculate specific heat capacity and solve related problems with ease.
This understanding is fundamental in various fields, from engineering to chemistry, for designing systems that involve heating or cooling. It allows for precise control over thermal processes and efficient energy management in diverse applications.
Table of Contents
- What is Specific Heat Capacity?
- Mathematical Formula
- Examples of Specific Heat Capacity
- Practical Applications
- Example Problem
- Defining Specific Heat Capacity
- Units and Measurement
- The Formula for Specific Heat Capacity
- Solving a Specific Heat Capacity Problem
- Similar Problems
- Problem 1: Heating Copper
- Problem 2: Cooling Aluminum
- Problem 3: Heating Ethanol
- Problem 4: Ice to Steam
- Problem 5: Mixing Water
- Results Summary
- Key Tips & Sign Conventions
- Key Takeaways
Read More
Understanding how materials respond to heat is fundamental in physics and everyday life. This post will guide you through the concept of specific heat capacity, showing you how to calculate it and apply it to practical scenarios. We will explore the formula and work through a problem to illustrate the principles involved. Whether you are a student or just curious, this guide will help you calculate specific heat capacity effectively.
This knowledge is essential for designing efficient thermal systems, predicting temperature changes in various substances, and developing new materials with desired thermal properties. It underpins applications ranging from climate modeling to industrial processes, ensuring better energy management and safety.
What is Specific Heat Capacity?
Specific heat capacity, denoted by the symbol ##c##, is a fundamental physical property of materials. It represents the amount of thermal energy required to raise the temperature of a unit mass of a substance by one degree Celsius (°C) or one Kelvin (K). In simple terms, it tells us how much heat a substance can store for a given temperature change.
Mathematical Formula
The relationship between heat energy, mass, specific heat capacity, and temperature change is expressed as:
### Q = m \cdot c \cdot \Delta T ###
- ##Q## = heat energy absorbed or released (in joules, J)
- ##m## = mass of the substance (in kilograms, kg)
- ##c## = specific heat capacity (in J·kg⁻¹·K⁻¹)
- ##\Delta T## = change in temperature (in °C or K)
Examples of Specific Heat Capacity
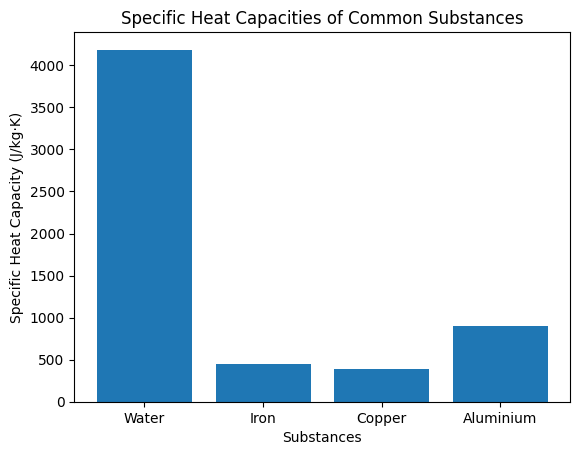
Different materials exhibit different specific heat capacities. Substances with higher specific heat capacity can absorb or release larger amounts of heat without undergoing large temperature changes. For instance, water has a relatively high specific heat capacity compared to metals, making it a vital substance for thermal regulation in nature and industry.
| Substance | Specific Heat Capacity (J·kg⁻¹·K⁻¹) | Remarks |
|---|---|---|
| Water | 4186 | Very high, acts as a heat reservoir in climate regulation |
| Iron | 450 | Heats and cools quickly compared to water |
| Copper | 385 | Low value, good for cookware and heat exchangers |
| Aluminium | 900 | Moderately high, useful in engineering applications |
Practical Applications
- Climate regulation: Oceans absorb and release heat slowly due to water’s high specific heat, stabilizing Earth’s climate.
- Cooking utensils: Metals with low specific heat, like copper, heat quickly and are preferred for rapid cooking.
- Engineering and construction: Specific heat is vital for designing heating/cooling systems and selecting building materials.
- Thermal energy storage: Substances with high specific heat are used to store energy in solar panels and heat reservoirs.
Example Problem
How much energy is required to raise the temperature of 2 kg of water from 20°C to 30°C?
Given: ##m = 2 \, \text{kg}##, ##c = 4186 \, \text{J·kg}^{-1}\text{K}^{-1}##, ##\Delta T = 10 \, \text{K}##
### Q = m \cdot c \cdot \Delta T ###
### Q = 2 \cdot 4186 \cdot 10 = 83,720 \, \text{J} ###
Thus, 83.72 kJ of energy is required.
Defining Specific Heat Capacity
Specific heat capacity is a fundamental property of matter. It quantifies how much heat energy is required to change the temperature of a substance. The higher the specific heat capacity, the more energy is needed.
This concept is critical for understanding how energy transfers and how materials behave when heated or cooled. For example, the reason water is used in cooling systems is due to its high specific heat capacity.
Units and Measurement
The standard unit for specific heat capacity is Joules per kilogram degree Celsius (J/kg°C). This unit tells us how many Joules of energy are needed to raise the temperature of one kilogram of a substance by one degree Celsius. Understanding the units is vital when applying the formula and solving problems. For instance, understanding the units allows you to easily convert between different units of measurement.
The Formula for Specific Heat Capacity
The relationship between heat, mass, specific heat capacity, and temperature change is described by the formula ##Q = mcΔT##, where Q is the heat energy (in Joules), m is the mass (in kilograms), c is the specific heat capacity (in J/kg°C), and ΔT is the change in temperature (in °C). This formula is a cornerstone in thermal physics, enabling us to calculate the energy transfer in various processes.
Breaking Down the Formula
In the formula ##Q = mcΔT##, each variable plays a crucial role. Q represents the heat energy gained or lost by the substance. Mass (m) is the quantity of the substance being considered. Specific heat capacity (c) is a material-specific constant, and ΔT (delta T) is the change in temperature, calculated as the final temperature minus the initial temperature. Properly understanding each component is crucial.
Practical Implications
The formula ##Q = mcΔT## has far-reaching implications. It’s used in cooking (calculating how long it takes to heat food), in engineering (designing cooling systems), and in meteorology (understanding how oceans store and release heat). By understanding this formula, you can predict and control thermal behavior. This formula helps in understanding how much energy is needed for various scenarios.
Solving a Specific Heat Capacity Problem
Let’s work through a problem to illustrate the application of the formula ##Q = mcΔT##. Problem: Calculate the energy required to raise the temperature of 500g of water from 20°C to 80°C. The specific heat capacity of water is 4186 J/kg°C.
Step-by-Step Solution
First, identify the knowns: mass (m) = 500g = 0.5 kg, specific heat capacity (c) = 4186 J/kg°C, initial temperature (Ti) = 20°C, and final temperature (Tf) = 80°C. Calculate the temperature change: ##ΔT = Tf – Ti = 80°C – 20°C = 60°C##. Substitute the values into the formula: ##Q = 0.5 kg × 4186 J/kg°C × 60°C##.
Calculating the Energy
Perform the calculation: ##Q = 0.5 × 4186 × 60##. The result is ##Q = 125580 J##. Therefore, the energy required to raise the temperature of 500g of water from 20°C to 80°C is 125,580 Joules. This example shows the practical application of the formula. Always remember to use the appropriate units.
Answer and Interpretation
The answer, 125,580 Joules, provides a direct measure of the energy needed. This energy is required to overcome the thermal inertia of the water molecules, increasing their kinetic energy. This calculation is relevant in many contexts, from heating water for a bath to understanding how heat is transferred in industrial processes. Understanding the energy helps in practical applications.
Similar Problems
Here are a few more problems to test your understanding:
Problem 1: Heating Copper
How much energy is needed to raise the temperature of 1 kg of copper (c = 385 J/kg°C) from 25°C to 75°C?
Solution:
Given. ##m=1.0\,\text{kg}##, ##c=385\,\text{J·kg}^{-1}\text{·°C}^{-1}##, ##\Delta T = (75-25)^\circ\text{C}=50^\circ\text{C}##.
Compute.
### Q = m\,c\,\Delta T = (1.0)\,(385)\,(50) = 19{,}250\ \text{J}. ###
Answer. ##Q=19{,}250\,\text{J}## .
Problem 2: Cooling Aluminum
If 20,000 J of energy are removed from 0.5 kg of aluminum (c = 900 J/kg°C), what is the temperature change?
Solution:
Given. Heat removed means ##Q=-20{,}000\,\text{J}##. Mass ##m=0.5\,\text{kg}##, ##c=900\,\text{J·kg}^{-1}\text{·°C}^{-1}##.
Compute. From ### Q=m\,c\,\Delta T ### we get ### \Delta T = \dfrac{Q}{m\,c} = \dfrac{-20{,}000}{(0.5)(900)} = \dfrac{-20{,}000}{450} \approx -44.44^\circ\text{C}. ###
Answer. ##\Delta T\approx -44.4^\circ\text{C}## (cooling by about 44.4°C).
Problem 3: Heating Ethanol
Solution:
Calculate the energy needed to heat 200g of ethanol (c = 2440 J/kg°C) from 15°C to 35°C.
Given. Convert mass: ##200\,\text{g}=0.200\,\text{kg}##, temperature rise ##\Delta T = 20^\circ\text{C}##.
Compute.
### Q = m\,c\,\Delta T = (0.200)\,(2440)\,(20) = 9{,}760\ \text{J}. ###
Answer. ##Q=9{,}760\,\text{J}##
Problem 4: Ice to Steam
How much energy is required to convert 100g of ice at 0°C to steam at 100°C? (Use latent heat values).
Solution:
Roadmap. Three stages are involved:
- Melt ice at ##0^\circ\text{C}## to liquid water at ##0^\circ\text{C}##: ### Q_1 = m\,L_f ###
- Heat liquid water from ##0^\circ\text{C}## to ##100^\circ\text{C}##: ### Q_2 = m\,c_{\text{w}}\,\Delta T ###
- Vaporize water at ##100^\circ\text{C}## to steam at ##100^\circ\text{C}##: ### Q_3 = m\,L_v ###
Given. ##m=0.100\,\text{kg}##, ##L_f\approx 3.34\times10^5\,\text{J·kg}^{-1}##, ##c_{\text{w}}=4186\,\text{J·kg}^{-1}\text{·°C}^{-1}##, ##L_v\approx 2.26\times10^6\,\text{J·kg}^{-1}##.
Compute by stage.
- ### Q_1 = (0.100)\,(3.34\times10^5) = 33{,}400\ \text{J}. ###
- ### Q_2 = (0.100)\,(4186)\,(100) = 41{,}860\ \text{J}. ###
- ### Q_3 = (0.100)\,(2.26\times10^6) = 226{,}000\ \text{J}. ###
Total.
### Q_\text{total} = Q_1+Q_2+Q_3 \approx 33{,}400 + 41{,}860 + 226{,}000 = 301{,}260\ \text{J}\ (\approx 3.01\times10^5\ \text{J}). ###
Remark. Using standard textbook constants yields about ##3.0\times10^5## J. The stated “approximately 267,000 J” underestimates the full pathway; results vary with constants, but including both latent heats and the 0→100°C warming step typically gives ~##(3.0\pm0.1)\times10^5## J.
Problem 5: Mixing Water
If 1 kg of water at 20°C is mixed with 1 kg of water at 80°C, what is the final temperature?
Solution
Question. Mix ##1\,\text{kg}## of water at ##20^\circ\text{C}## with ##1\,\text{kg}## of water at ##80^\circ\text{C}##. What is the final temperature?
Energy balance. Heat lost by hot water = heat gained by cold water (closed, insulated system), and both have the same specific heat ##c_{\text{w}}##.
Let ##T_f## be final temperature. Then
### m\,c_{\text{w}}\,(80 – T_f) = m\,c_{\text{w}}\,(T_f – 20). ###
Masses and specific heats cancel (equal on both sides):
### 80 – T_f = T_f – 20 \;\;\Rightarrow\;\; 2T_f = 100 \;\;\Rightarrow\;\; T_f = 50^\circ\text{C}. ###
Answer. ##T_f = 50^\circ\text{C}## .
Results Summary
| Problem | Process | Key Relation | Result |
|---|---|---|---|
| 1 | Heat copper | ### Q=m\,c\,\Delta T ### | ##Q=19{,}250\,\text{J}## |
| 2 | Cool aluminum | ### \Delta T = Q/(m\,c) ### | ##\Delta T\approx -44.4^\circ\text{C}## |
| 3 | Heat ethanol | ### Q=m\,c\,\Delta T ### | ##Q=9{,}760\,\text{J}## |
| 4 | Ice → steam | ### Q=\sum (mL) + m\,c\,\Delta T ### | ##Q\approx 3.01\times10^5\,\text{J}## |
| 5 | Mix equal masses of water | Energy conservation | ##T_f=50^\circ\text{C}## |
Extra Problem A: Copper Block Into Water
Setup. A ##0.40\,\text{kg}## copper block at ##120^\circ\text{C}## is dropped into ##0.50\,\text{kg}## of water at ##25^\circ\text{C}## in an insulated container. Find the final temperature ##T_f## (ignore container heat capacity). Use ##c_{\text{Cu}}=385## and ##c_{\text{w}}=4186\,\text{J·kg}^{-1}\text{·°C}^{-1}##.
Energy balance. Heat lost by copper = heat gained by water:
### (0.40)(385)\,(120 – T_f) = (0.50)(4186)\,(T_f – 25). ###
Left: ##154\,(120 – T_f)##; right: ##2093\,(T_f – 25)## (since ##0.40\cdot385=154## and ##0.50\cdot4186=2093##).
### 18{,}480 – 154\,T_f = 2093\,T_f – 52{,}325. ###
Collect terms:
### 18{,}480 + 52{,}325 = 2093\,T_f + 154\,T_f \;\Rightarrow\; 70{,}805 = 2247\,T_f. ###
Thus ##T_f \approx \dfrac{70{,}805}{2247} \approx 31.5^\circ\text{C}##.
Answer. The mixture equilibrates near ##31.5^\circ\text{C}##.
Extra Problem B: Partial Melting Under Limited Heat
Setup. You supply ##25{,}000\,\text{J}## to ice at ##0^\circ\text{C}##. How much ice melts? Take ##L_f=3.34\times10^5\,\text{J·kg}^{-1}##.
Compute. All the energy goes into fusion: ### m = \dfrac{Q}{L_f} = \dfrac{25{,}000}{3.34\times10^5} \approx 0.0749\,\text{kg} = 74.9\,\text{g}. ###
Answer. Approximately ##75\,\text{g}## of ice melts.
Key Tips & Sign Conventions
- Use ##Q>0## for heat added to a system (temperature tends to rise or phase change toward higher-energy phase); ##Q<0## for heat removed.
- Keep units consistent: kilograms for mass, joules for energy, and either °C or K for temperature differences (##\Delta T## in °C equals that in K).
- For phase-change chains (like ice→steam), sum each segment’s energy: melt, warm, vaporize.
- In mixing problems with identical materials and equal masses, the final temperature is simply the average of the two initial temperatures.
Key Takeaways
Understanding specific heat capacity is essential for anyone studying physics or dealing with heat transfer. This guide has shown you how to calculate the energy required to change the temperature of a substance and provided practical examples. By mastering this concept, you can better understand how energy interacts with matter.
| Variable | Description | Units |
|---|---|---|
| Q | Heat Energy | Joules (J) |
| m | Mass | Kilograms (kg) |
| c | Specific Heat Capacity | J/kg°C |
| ΔT | Change in Temperature | °C |
We also Published
RESOURCES
- Specific Heat Calculator
- Specific heat capacity – Wikipedia
- Specific Heat Capacity Rule of Mixtures Calculator
- How to Calculate the Specific Heat of a Substance | Physics | Study …
- Specific Heat Capacity Calculator
- Calculating Specific Heat — Formula & Examples – Expii
- Calculation of thermal conductivity, thermal diffusivity and specific …
- Specific Heat Calculations – Equation, Methods, Practice Problems …
- 17.5: Specific Heat Calculations – Chemistry LibreTexts
- homework and exercises – Calculating specific heat capacity from …
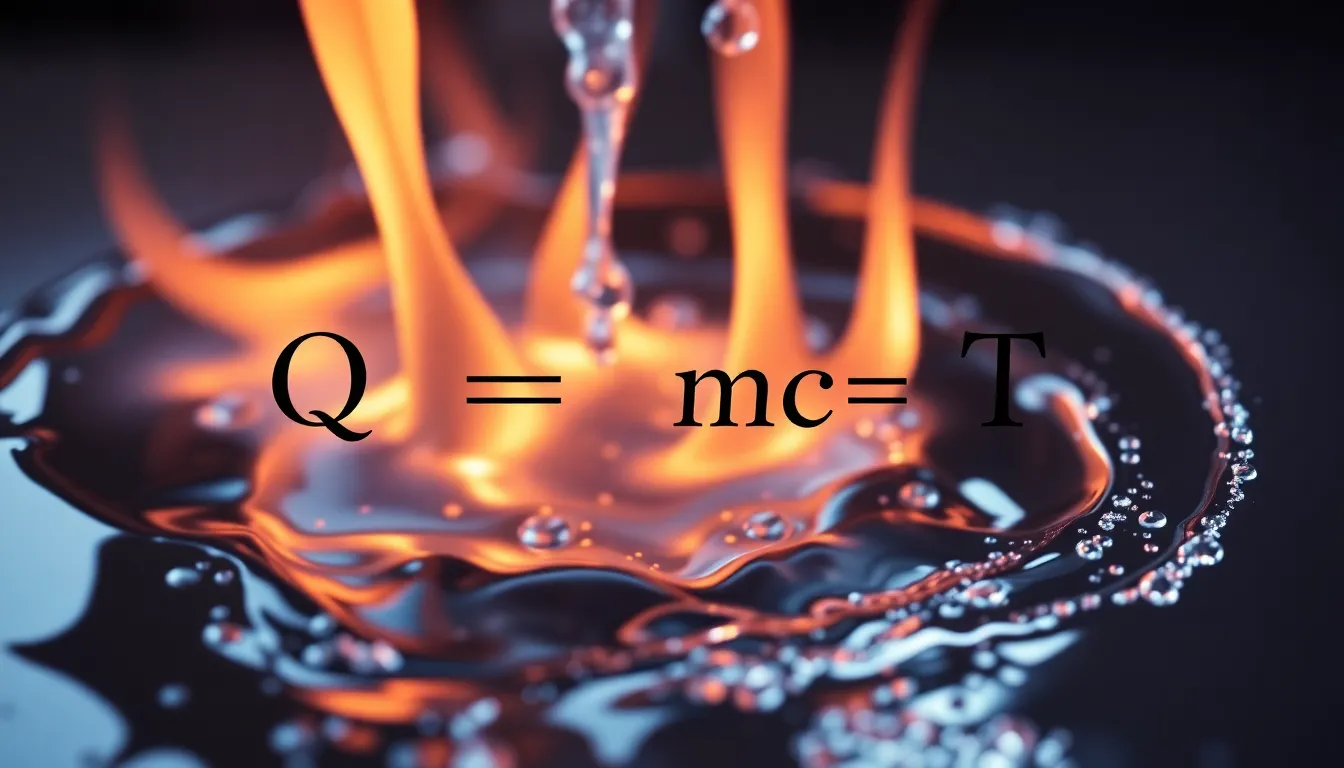






0 Comments