The principles of work, energy, and power are fundamental in physics, particularly for competitive exams like IIT JEE. IIT JEE work energy problems often require a deep understanding of energy conservation and transformation. This post delves into practical examples and numerical solutions to help you master these concepts and excel in your studies.
Table of Contents
Read More
Let’s dive into the exciting world of physics, where we’ll unravel the principles of work and energy as they apply to the IIT JEE exam. This exploration will equip you with the skills to tackle complex numerical problems, solidifying your understanding of energy transformations and mechanical systems. Get ready to enhance your problem-solving abilities!
Understanding Work and Energy Concepts
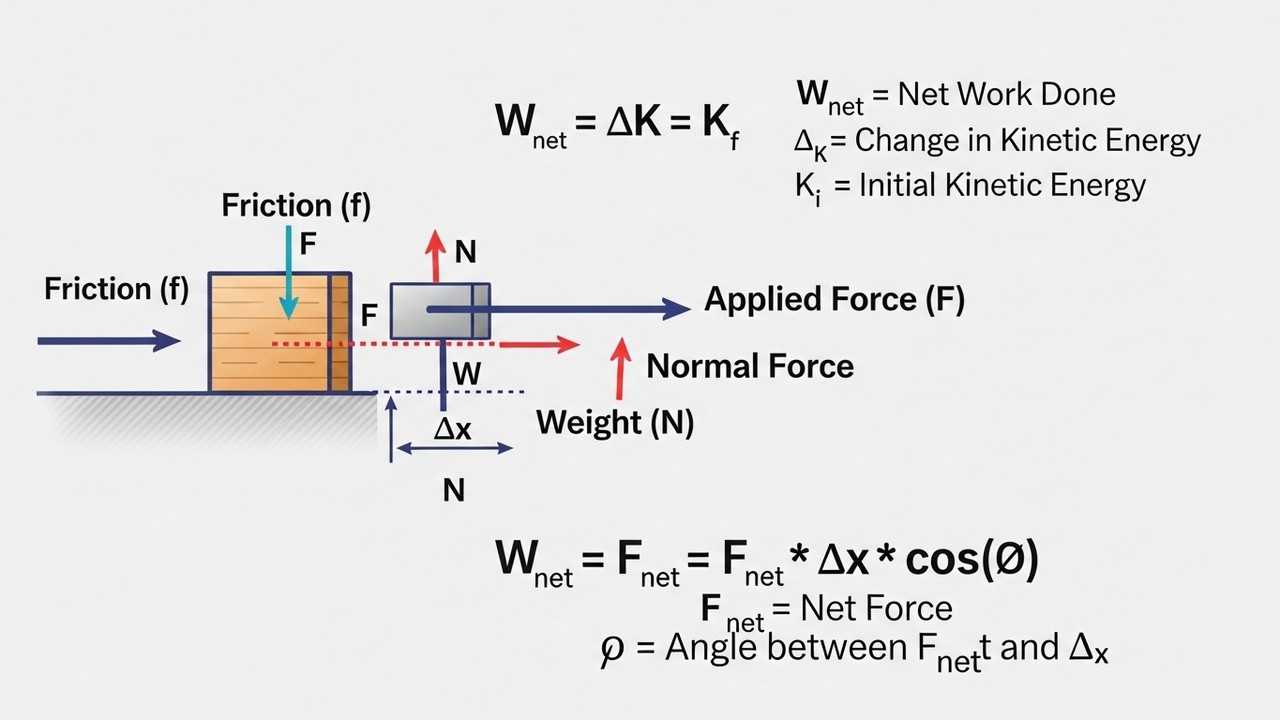
To begin, consider the fundamental concepts of work and energy. Work, in physics, is defined as the transfer of energy that occurs when an object is moved by a force. Energy, on the other hand, is the capacity to do work. These concepts are intertwined through the work-energy theorem, a cornerstone principle in mechanics. This theorem states that the net work done on an object equals the change in its kinetic energy.
Work Done by a Constant Force
When a constant force acts on an object, the work done is straightforward to calculate. It’s the product of the force and the displacement of the object in the direction of the force. Mathematically, this is represented as ##W = F \cdot d \cdot cos(\theta)##, where ##W## is work, ##F## is the force, ##d## is the displacement, and ##\theta## is the angle between the force and the displacement. This formula highlights how the direction of the force relative to the displacement impacts the work done. For instance, if the force is perpendicular to the displacement, no work is done.
Understanding the nuances of work done by constant forces is pivotal. Consider a scenario where a box is pushed across a floor. The force applied, the distance covered, and the angle at which the force is applied all influence the amount of work done. Friction often plays a role, subtracting from the work done by the applied force. This detailed understanding helps in solving complex problems related to work done by multiple forces.
Kinetic and Potential Energy
Kinetic energy is the energy an object possesses due to its motion, given by ##KE = \frac{1}{2}mv^2##, where ##m## is mass and ##v## is velocity. Potential energy, however, is stored energy due to an object’s position or configuration. Gravitational potential energy, for instance, is given by ##PE = mgh##, where ##g## is the acceleration due to gravity and ##h## is the height. The law of conservation of energy states that the total energy in a closed system remains constant; energy can transform between different forms, but it is neither created nor destroyed.
The interplay between kinetic and potential energy is crucial in solving problems. For example, when a ball is thrown upwards, its kinetic energy is converted into gravitational potential energy as it ascends. Conversely, as the ball falls, potential energy converts back into kinetic energy. In mechanical systems, understanding these energy transformations allows for accurate predictions of motion and energy changes, which is fundamental for IIT JEE problem-solving. This understanding is key to mastering work and energy problems.
Applying Work-Energy Principles to Numerical Problems
The application of work-energy principles is best understood through solving numerical problems. These problems often involve calculating work done by various forces, determining changes in kinetic and potential energy, and applying the work-energy theorem. Practice with different problem types is essential to building a strong foundation.
Example Problem: Calculating Work Done
We calculate the work done by a force applied at an angle using the formula:
###W = F \cdot d \cdot \cos(\theta)###
Here, a block of mass 5 kg is pulled along a horizontal surface by a force of 20 N at an angle of 30° above the horizontal, over a distance of 10 m.
Substituting values:
###W = 20\,N \cdot 10\,m \cdot \cos(30^\circ)###
Since ###\cos(30^\circ) = \tfrac{\sqrt{3}}{2} \approx 0.866###:
###W = 200 \cdot 0.866 \approx 173.2\,J###
Thus, the work done by the applied force is approximately 173.2 Joules. This example shows how to calculate work when a force acts at an angle, a key concept for IIT JEE physics circuits and mechanics problems.
In a practical application, consider the role of friction. If a frictional force of 5 N opposes the motion, we would need to calculate the work done by friction, which is negative since it acts in the opposite direction. The net work done on the block would then be the sum of the work done by the applied force and the work done by friction. This demonstrates how to apply the work-energy theorem in a comprehensive way, considering all forces involved in the system.
Work-Energy Theorem in Action
We apply the work-energy theorem: ###W = \Delta KE###
First, calculate the initial kinetic energy:
###KE_i = \tfrac{1}{2} m v_i^2 = \tfrac{1}{2} \cdot 1000\,kg \cdot (20\,m/s)^2 = 200{,}000\,J###
The final kinetic energy is zero because the car comes to rest. So the work done by the braking force is:
###W = KE_f – KE_i = 0 – 200{,}000 = -200{,}000\,J###
Now, distance travelled during braking is:
###d = v_i \cdot t = 20\,m/s \cdot 5\,s = 100\,m###
Using the work formula:
###W = F \cdot d \quad \Rightarrow \quad F = \dfrac{W}{d} = \dfrac{-200{,}000}{100} = -2000\,N###
The negative sign indicates that the braking force is opposite to the direction of motion. Thus, the magnitude of the braking force is **2000 N**.
This calculation shows the direct relationship between work done, kinetic energy, and the force applied. The negative work done indicates that the braking force removes kinetic energy from the system, causing the car to decelerate. This example demonstrates how to use the work-energy theorem to solve real-world problems involving motion and force. Understanding the theorem is key for IIT JEE work energy problems.
Final Word: Mastering Work-Energy Problems
Mastering work and energy concepts is crucial for success in the IIT JEE exam. The ability to apply the work-energy theorem, calculate work done by various forces, and understand energy transformations are essential skills. Consistent practice with a variety of problems will help you build confidence and proficiency. Remember to always consider all forces acting on an object, and to correctly apply the formulas for work, kinetic energy, and potential energy.
Similar Problems (Quick Solutions)
Problem 1
A 2 kg object is lifted 5 m. How much work is done against gravity? Answer: 98 J
Problem 2
A spring with a spring constant of 100 N/m is stretched 0.2 m. What is the potential energy stored? Answer: 2 J
Problem 3
A 10 kg object moves at 4 m/s. What is its kinetic energy? Answer: 80 J
Problem 4
A force of 15 N moves an object 3 m in the direction of the force. How much work is done? Answer: 45 J
Problem 5
A car accelerates from rest to 20 m/s. If its mass is 1500 kg, what is the change in kinetic energy? Answer: 300,000 J
| Concept | Formula | Description |
|---|---|---|
| Work Done | ##W = F \cdot d \cdot cos(\theta)## | Work done by a force is the product of the force, displacement, and the cosine of the angle between them. |
| Kinetic Energy | ##KE = \frac{1}{2}mv^2## | The energy an object possesses due to its motion, dependent on mass and velocity. |
| Potential Energy (Gravitational) | ##PE = mgh## | The energy stored in an object due to its position, dependent on mass, gravity, and height. |
| Work-Energy Theorem | ##W = \Delta KE## | The net work done on an object equals the change in its kinetic energy. This is vital for **work and energy** calculations. |
We also Published
RESOURCES
- WORK, ENERGY AND POWER | MasterJEE Classes
- Work, Power and Energy (WPE) – YouTube
- Complete List of Prerequisites for Every Chapter in JEE : r …
- Work Energy Theorem -Study Material for IIT JEE | askIITians
- Work Energy and Power Revision Notes for JEE & Boards
- IIT JEE advanced Physics -Work, Energy & Power- Study Materials
- Work Power & Energy | Physics | JEE Main Previous Year Questions …
- Work Power Energy JEE Main Previous Year Questions With Solutions
- Work Energy and Power Class 11 Physics Notes – IIT JEE | NEET …
- Work Power Energy Practice Problems | JEE Advanced






0 Comments