The evaluation of limits is a core concept in calculus, providing insights into function behavior. Trigonometric Limit problems, specifically those involving sine and cosine, often require specific techniques to solve. We’ll explore a common type of problem and provide a detailed, step-by-step guide for finding the solution. This process highlights the importance of understanding fundamental limit theorems.
Table of Contents
- Similar Problems and Quick Solutions
- Problem 1: Evaluate ##\lim_{x \to 0} \frac{{\sin(3x)}}{x}##
- Problem 2: Evaluate ##\lim_{x \to 0} \frac{{\tan(2x)}}{x}##
- Problem 3: Evaluate ##\lim_{x \to 0} \frac{{\sin(x)}}{{\sin(2x)}}##
- Problem 4: Evaluate ##\lim_{x \to 0} \frac{{\sin^2(x)}}{x^2}##
- Problem 5: Evaluate ##\lim_{x \to 0} \frac{{\sin(ax)}}{{\sin(bx)}}##
Read More
Let’s explore the evaluation of a Trigonometric Limit. This fundamental concept is essential in calculus and helps us understand the behavior of functions near specific points. We’ll break down the process step-by-step, providing clarity and insights into the underlying principles. Our primary focus will be on the limit involving the sine function.
Understanding the Trigonometric Limit Problem
The core of our task involves finding the limit of ##\frac{{\sin(5x)}}{x}## as ##x## approaches 0. This is a classic problem in calculus that showcases the relationship between trigonometric functions and limits. The direct substitution of ##x = 0## results in an indeterminate form, which makes direct evaluation impossible.
To solve this, we need to employ trigonometric identities and limit theorems. We will be utilizing the standard limit result: ##\lim_{x \to 0} \frac{{\sin(x)}}{x} = 1##. This fundamental result forms the basis for solving more complex trigonometric limits.
Solution: Evaluating the Trigonometric Limit
Step 1: Manipulating the Expression
To apply the standard limit, we need to manipulate the given expression ##\frac{{\sin(5x)}}{x}##. We can rewrite it to resemble the standard form. We multiply and divide by 5 to get the required form. This transformation is crucial for applying the known limit rule effectively.
The manipulation involves introducing a factor of 5 both in the numerator and the denominator. This allows us to transform the expression into a form where we can directly apply the standard trigonometric limit. This step is key to simplifying the original expression.
Step 2: Applying the Limit
We can rewrite the original limit as: ##\lim_{x \to 0} \frac{{\sin(5x)}}{x} = \lim_{x \to 0} 5 \cdot \frac{{\sin(5x)}}{5x}##. Now, let ##u = 5x##. As ##x \to 0##, ##u \to 0##. The limit becomes: ##\lim_{u \to 0} 5 \cdot \frac{{\sin(u)}}{u}##.
Using the known limit ##\lim_{u \to 0} \frac{{\sin(u)}}{u} = 1##, we can simplify the expression. The substitution helps in aligning the expression with a form that is known to converge to 1. This simplification is critical for finding the final value.
Final Solution
The final result is: ##\lim_{x \to 0} \frac{{\sin(5x)}}{x} = 5 \cdot 1 = 5##. The Trigonometric Limit of the given function is 5. This means that as x approaches 0, the function approaches the value 5.
The limit of the function ##\frac{{\sin(5x)}}{x}## as ##x## approaches 0 is indeed 5. This result is obtained by strategically manipulating the original expression and applying known limit rules. The final answer showcases the function’s behavior near the point in question.
Similar Problems and Quick Solutions
Problem 1: Evaluate ##\lim_{x \to 0} \frac{{\sin(3x)}}{x}##
Solution: 3
Problem 2: Evaluate ##\lim_{x \to 0} \frac{{\tan(2x)}}{x}##
Solution: 2
Problem 3: Evaluate ##\lim_{x \to 0} \frac{{\sin(x)}}{{\sin(2x)}}##
Solution: 0.5
Problem 4: Evaluate ##\lim_{x \to 0} \frac{{\sin^2(x)}}{x^2}##
Solution: 1
Problem 5: Evaluate ##\lim_{x \to 0} \frac{{\sin(ax)}}{{\sin(bx)}}##
Solution: ##\frac{a}{b}##
| Concept | Description | Application in **Trigonometric Limit** |
|---|---|---|
| Standard Limit | ##\lim_{x \to 0} \frac{{\sin(x)}}{x} = 1## | Used to simplify and evaluate the given expression. |
| Substitution | Substituting a variable to simplify the expression. | Helps transform the expression into a known form. |
| Trigonometric Identities | Using identities to manipulate the trigonometric functions. | Used to rewrite the expression into a more manageable form. |
We also Published
RESOURCES
- Limits of Trigonometric Functions – YouTube
- 2.7: Limit of Trigonometric functions – Mathematics LibreTexts
- Calculus – How to find trigonometric limits using sin(x)/x – YouTube
- [College Calculus: Limits] Solving for Trigonometric Limits. How did …
- Calculus 1: Finding Limits of Trigonometric Functions | Math with …
- Limits of Trigonometric Functions Formulas
- Limits Involving Trigonometric Functions
- can someone please explain to me how to do limits with trig …
- Calculus I – Proof of Trig Limits
- trigonometry – Trigonometric Limit without L’Hopital – Mathematics …
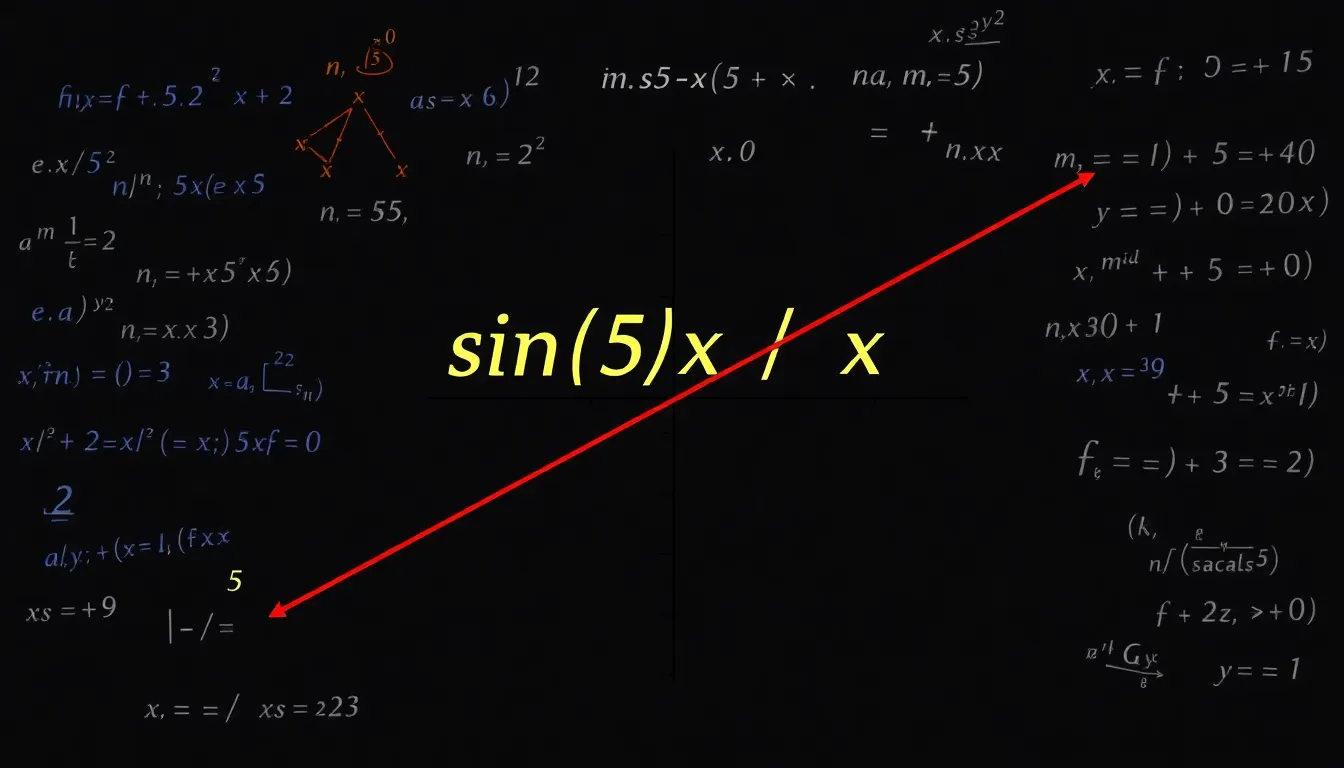




0 Comments