Properties of Real Numbers form the very backbone of mathematical understanding. Real Number Properties are essential for anyone seeking to excel in algebra, calculus, and beyond. These properties, though seemingly simple, are the foundation upon which more complex mathematical concepts are built. The ability to manipulate and understand these properties is not only crucial for solving equations but also for grasping the underlying structure and logic of mathematics. As we delve into the properties, from closure to the distributive law, we’ll uncover how they shape our understanding of numbers and their relationships.

The properties of real numbers form the bedrock of algebra and calculus. Grasping these fundamental concepts is crucial for anyone venturing into higher mathematics. This blog post meticulously explores these essential properties, providing a clear and comprehensive understanding of their significance and application. We will navigate through the concepts of closure, commutativity, associativity, the distributive law, identity and inverse elements, and the absolute value, all while emphasizing the utility of these properties in algebraic manipulations. The goal is to furnish you with a robust foundation, empowering you to tackle more complex mathematical problems with confidence.

Understanding Closure Property

The Real Number Properties begin with the concept of closure. The closure property states that when you perform an operation (addition or multiplication) on two real numbers, the result is also a real number. For addition, if you add any two real numbers, the sum is always a real number. For example, if you add 2 and 3, both real numbers, the sum is 5, which is also a real number. Similarly, if you multiply any two real numbers, the product is always a real number. This fundamental property ensures that the real number system is self-contained under these operations, making it a consistent framework for mathematical operations. The closure property is a cornerstone, ensuring that operations within the real number system remain within the system itself.

Examples of Closure

Consider the following examples to solidify your understanding of the closure property. Adding two integers, like 7 and -2, results in 5, an integer. Multiplying two fractions, such as 1/2 and 3/4, yields 3/8, a fraction. These examples demonstrate that both addition and multiplication operations, when applied to real numbers, always produce a real number. This property is not always true for other number systems or operations. For instance, division of integers does not always result in an integer. The closure property, therefore, highlights the unique characteristics of the real number system, where these operations consistently produce results within the same set.

Closure in Different Contexts

The concept of closure extends beyond simple addition and multiplication. It is a critical concept in various areas of mathematics, including set theory and abstract algebra. In set theory, a set is closed under an operation if performing that operation on elements within the set always results in another element of the same set. In abstract algebra, groups, rings, and fields are defined based on closure properties under specific operations. Understanding closure provides a foundational principle for understanding the structure and behavior of mathematical systems. It is a fundamental property that guarantees the consistency and predictability of mathematical operations within the real number system.

Implications of Closure

The implications of the closure property are far-reaching. It ensures that mathematical operations within the real number system are well-defined and consistent. Without this property, the structure of algebra and calculus would become unreliable. This property is fundamental to the development of mathematical theories and proofs. It provides a stable foundation upon which more complex mathematical concepts are built. The consistent nature of the real number system, guaranteed by the closure property, allows mathematicians to develop reliable models and solutions to a wide range of problems. The closure property, though seemingly simple, is a cornerstone of mathematical consistency.

Commutativity and Associativity

Continuing with our exploration of Real Number Properties, we delve into commutativity and associativity, which describe how the order and grouping of numbers affect addition and multiplication. Commutativity states that the order in which you add or multiply real numbers does not affect the result. For example, 2 + 3 is the same as 3 + 2, and 2 × 3 is the same as 3 × 2. Associativity goes further, saying that the way you group numbers in addition or multiplication doesn’t matter. For instance, (2 + 3) + 4 is the same as 2 + (3 + 4), and (2 × 3) × 4 is the same as 2 × (3 × 4). These properties greatly simplify algebraic manipulations and allow us to rearrange terms as needed.

Detailed Explanation of Commutativity

Commutativity is a straightforward concept, but it is incredibly powerful in practice. It tells us that the sequence of operations does not matter when adding or multiplying real numbers. This property simplifies calculations and proofs, allowing for flexibility in how we approach mathematical problems. For example, when calculating the total cost of items, the order in which you add the prices doesn’t affect the final sum. This principle is a key component of algebra, allowing us to rearrange terms and simplify equations with ease. It provides a fundamental understanding of how addition and multiplication behave, ensuring that the outcome remains consistent regardless of the arrangement.

Detailed Explanation of Associativity

Associativity extends the concept of commutativity by stating that the grouping of numbers in addition or multiplication does not affect the result. Consider the expression (5 + 3) + 2. We can group it as (5 + 3) + 2 or 5 + (3 + 2) and still arrive at the same answer. Similarly, with multiplication: (2 × 4) × 3 is the same as 2 × (4 × 3). This property is crucial in simplifying complex expressions and equations. It allows us to strategically group terms to make calculations easier or to reveal underlying patterns. Understanding associativity provides flexibility in problem-solving, allowing us to choose the most efficient method for any given calculation.

Commutativity and Associativity in Action

Let’s look at practical examples to see these properties in action. Suppose you need to add 7, 5, and 3. Using commutativity, you can rearrange the order to 3 + 5 + 7, or any other order, without changing the result. Using associativity, if you have (12 × 2) × 3, you can regroup as 12 × (2 × 3) to simplify the calculation. These properties are not only useful in basic arithmetic but also in more advanced algebra and calculus, where complex equations can be simplified by strategically rearranging and regrouping terms. These properties are essential tools for effective mathematical manipulation.

Limitations and Non-Applicability

It is important to note that not all mathematical operations are commutative or associative. Subtraction and division, for example, are not commutative. 5 – 3 is not the same as 3 – 5, and 6 ÷ 2 is not the same as 2 ÷ 6. Similarly, subtraction and division are not associative. (8 – 4) – 2 is not the same as 8 – (4 – 2), and (12 ÷ 6) ÷ 2 is not the same as 12 ÷ (6 ÷ 2). Recognizing the limitations of these properties is crucial for avoiding errors in calculations and understanding the scope of their applicability. Only addition and multiplication of real numbers are commutative and associative.

The Distributive Law Explained

The Real Number Properties include the distributive law, which is a fundamental concept that links multiplication and addition. The distributive law states that multiplying a number by a sum is the same as multiplying the number by each term in the sum and then adding the products. Mathematically, this is represented as a(b + c) = ab + ac. This law is essential for simplifying expressions, expanding brackets, and solving equations. It allows us to break down complex calculations into simpler steps, making algebraic manipulation more manageable and efficient. The distributive law is a crucial tool in algebra and is fundamental to many mathematical operations.

Breaking Down the Distributive Law

To understand the distributive law, consider an example: 2(3 + 4). According to the distributive law, this can be expanded as 2 × 3 + 2 × 4, which equals 6 + 8, resulting in 14. Without the distributive law, you would first have to compute the sum inside the parentheses (3 + 4 = 7) and then multiply by 2 (2 × 7 = 14). The distributive law allows you to bypass this step and perform the multiplication directly. This becomes particularly useful when dealing with variables or more complex expressions, where simplifying inside parentheses is not always straightforward. The distributive law simplifies complex algebraic expressions.

Applications in Algebra

The distributive law is extensively used in algebra for various operations. It is vital for expanding expressions, simplifying equations, and solving for unknowns. When dealing with equations like 3(x + 2) = 15, the distributive law allows us to expand the left side to 3x + 6 = 15, making it easier to isolate the variable x. It is also used in factoring, where we work in reverse, identifying common factors to rewrite expressions in a simpler form. The ability to distribute multiplication over addition is a cornerstone of algebraic manipulation, streamlining problem-solving and enabling more advanced mathematical techniques. The distributive law is an indispensable tool in algebra.

Practical Examples

Let’s look at some practical examples to demonstrate the distributive law. Suppose you have the expression 4(x – 3). Using the distributive law, you expand this to 4x – 12. Consider another example: 5(2y + 1). Expanding this gives you 10y + 5. These examples illustrate how the distributive law simplifies expressions by eliminating parentheses and making it easier to manipulate the terms. This simplification is crucial for solving equations and understanding relationships between variables. The distributive law provides a systematic approach to manipulating algebraic expressions.

Common Mistakes and Tips

One common mistake when applying the distributive law is forgetting to distribute the multiplication over all terms inside the parentheses. For example, in the expression 2(x + y – 3), it’s crucial to multiply 2 by each term: 2x + 2y – 6. Another mistake is mixing up the sign of the terms. Always ensure that the sign of the term is correctly applied when multiplying. Practicing various examples and carefully checking your work are essential to avoid these common errors. Understanding the distributive law requires careful attention to detail. The key is to systematically multiply each term inside the parentheses by the factor outside.

Additive and Multiplicative Identities

The Real Number Properties include the additive and multiplicative identities, which are fundamental concepts in arithmetic. The additive identity is the number zero (0), and it has the property that adding it to any real number does not change that number. For example, 5 + 0 = 5. The multiplicative identity is the number one (1), and multiplying any real number by one does not change that number. For example, 7 × 1 = 7. These identities are essential because they define the neutral elements for addition and multiplication, providing a foundation for algebraic operations. These identities are critical for understanding the behavior of numbers in mathematical operations.

The Role of Zero (Additive Identity)

Zero (0) is the additive identity because it leaves any number unchanged when added. This property is essential in arithmetic and algebra. It simplifies operations and helps in solving equations. When a number is added to its additive inverse (negative counterpart), the result is always zero. This concept is fundamental to balancing equations and solving for unknown variables. The additive identity is a fundamental concept that underpins many mathematical operations.

The Role of One (Multiplicative Identity)

One (1) is the multiplicative identity because multiplying any number by one leaves the number unchanged. This property is crucial for simplifying expressions and solving equations. It provides a neutral element that does not alter the value of the expression when multiplied. The multiplicative identity is also essential in understanding the concept of multiplicative inverses. When a number is multiplied by its multiplicative inverse (reciprocal), the result is always one. This concept is fundamental to dividing fractions and solving for unknown variables. The multiplicative identity is a cornerstone of multiplicative operations.

Practical Implications

The additive and multiplicative identities are essential tools in mathematical manipulations. They are used extensively in simplifying expressions, solving equations, and proving mathematical theorems. For example, if you have an equation like x + 0 = 5, the additive identity allows you to simplify it to x = 5. Similarly, if you have an equation like 7 × 1 = x, the multiplicative identity allows you to simplify it to x = 7. These identities are fundamental to understanding the behavior of numbers and performing mathematical operations. The additive and multiplicative identities are indispensable tools in mathematics.

Examples in Action

Let’s illustrate these identities with some examples. If you add 0 to any number, such as 10, the result is still 10. If you multiply any number by 1, such as 15 × 1, the result is still 15. These examples highlight the fundamental roles of these identities in maintaining the value of numbers during mathematical operations. These identities are not only useful in basic arithmetic but also play a critical role in more advanced mathematical concepts, such as linear algebra and calculus. The additive and multiplicative identities are essential for efficient and accurate calculations.

Additive and Multiplicative Inverses

The Real Number Properties include additive and multiplicative inverses, which are fundamental concepts in algebra. The additive inverse of a number is its negative counterpart, which, when added to the original number, results in zero. For example, the additive inverse of 5 is -5, since 5 + (-5) = 0. The multiplicative inverse of a number is its reciprocal, which, when multiplied by the original number, results in one. For example, the multiplicative inverse of 2 is 1/2, since 2 × (1/2) = 1. Understanding inverses is crucial for solving equations and simplifying expressions. These inverses enable us to manipulate equations effectively.

Understanding Additive Inverses

The additive inverse is also known as the opposite of a number. It is the number that, when added to the original number, yields zero. This property is essential in solving equations because it allows us to isolate variables. For example, to solve the equation x + 3 = 7, we can add the additive inverse of 3, which is -3, to both sides of the equation, resulting in x = 4. This concept is a cornerstone of algebraic manipulation. The additive inverse enables us to balance equations. The additive inverse is a crucial concept in algebra.

Understanding Multiplicative Inverses

The multiplicative inverse, also known as the reciprocal, is the number that, when multiplied by the original number, gives a product of one. For example, the multiplicative inverse of 4 is 1/4, since 4 × (1/4) = 1. This property is essential for dividing fractions and solving equations involving multiplication. To solve the equation 2x = 8, we can multiply both sides by the multiplicative inverse of 2, which is 1/2, resulting in x = 4. The multiplicative inverse is a fundamental tool in algebra, enabling us to solve equations involving multiplication and division. The multiplicative inverse is vital for simplifying expressions.

Practical Applications

The additive and multiplicative inverses are used extensively in algebra for solving equations and simplifying expressions. They are essential tools for manipulating equations and isolating variables. For instance, to solve the equation x + 5 = 10, you use the additive inverse of 5, which is -5, to isolate x. Similarly, in the equation 3x = 12, you use the multiplicative inverse of 3, which is 1/3, to isolate x. Understanding and applying these inverses is fundamental to algebraic problem-solving. The correct use of these inverses ensures accurate and efficient calculations.

Examples and Clarifications

Let’s look at some specific examples. The additive inverse of -7 is 7, and the multiplicative inverse of 1/3 is 3. In solving equations, these inverses are essential. For example, if we have x – 4 = 9, adding the additive inverse of -4 (which is 4) to both sides gives us x = 13. If we have (1/2)x = 6, multiplying both sides by the multiplicative inverse of 1/2 (which is 2) gives us x = 12. These examples demonstrate how inverses are crucial for manipulating equations and solving for unknown variables. The consistent use of inverses is essential in mathematical calculations.

Absolute Value and Its Properties

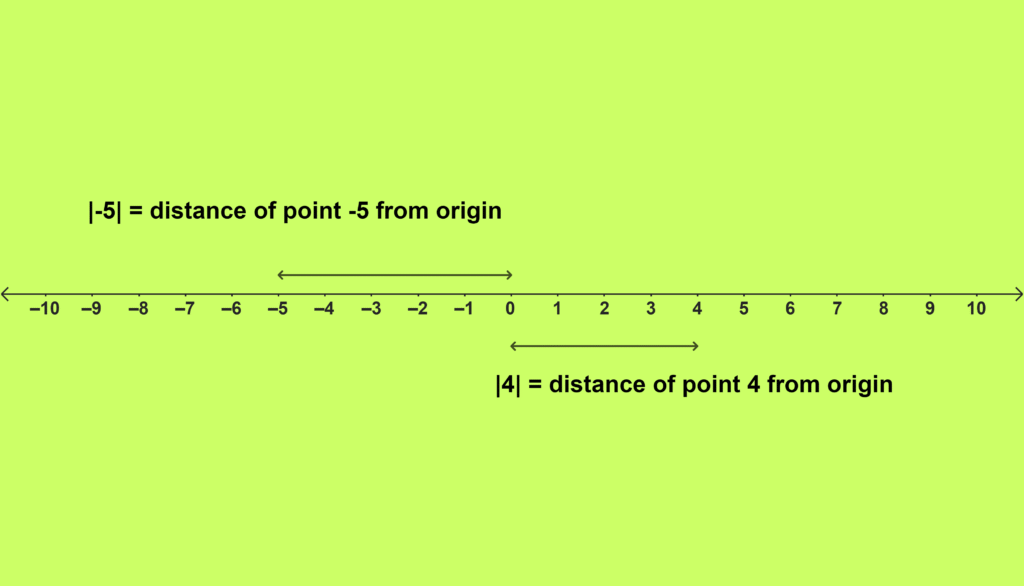
The Real Number Properties include the absolute value and its properties, which are essential for understanding distances and magnitudes. The absolute value of a real number is its distance from zero on the number line, regardless of its sign. This means the absolute value of a positive number is the number itself, and the absolute value of a negative number is its positive counterpart. For example, |5| = 5 and |-5| = 5. Understanding absolute value is crucial for solving equations and inequalities. The concept helps to define the magnitude of a number.

Defining Absolute Value

The absolute value is denoted by vertical bars: |x|. It represents the magnitude or distance of a number from zero on the number line. The key property of absolute value is that it always results in a non-negative value. Whether the original number is positive or negative, its absolute value is always positive or zero. This property is particularly useful in various mathematical contexts, including geometry, physics, and engineering. The absolute value simplifies measurements and calculations. The absolute value provides a clear understanding of magnitudes.

Properties of Absolute Value

Several properties of absolute value are essential to understand.

• |a| ≥ 0 for all real numbers a.
• |a| = |-a|; the absolute value of a number is the same as the absolute value of its negative.
• |ab| = |a||b|; the absolute value of a product is the product of the absolute values.
• |a/b| = |a|/|b|, if b ≠ 0; the absolute value of a quotient is the quotient of the absolute values.

These properties are crucial for simplifying and solving equations involving absolute values. The properties of absolute value simplify complex problems.

Solving Equations with Absolute Value

Solving equations involving absolute values often requires considering multiple cases. For example, the equation |x – 3| = 5 means that x – 3 can be either 5 or -5. Therefore, we have two possible solutions: x – 3 = 5, which gives x = 8, and x – 3 = -5, which gives x = -2. It is important to consider both positive and negative possibilities. Equations involving absolute values can be more complex, but by systematically considering the different cases, you can find all solutions. The absolute value equations require careful consideration of the signs.

Practical Examples

Let’s look at a few practical examples. If |x| = 4, then x can be either 4 or -4. If |2x – 1| = 3, then 2x – 1 can be 3 or -3. Solving each case, we get 2x – 1 = 3, which gives x = 2, and 2x – 1 = -3, which gives x = -1. These examples illustrate how to solve equations involving absolute values. It is essential to consider all possible scenarios. The absolute value equations require systematic problem-solving.

Inequalities and Intervals

The Real Number Properties include the concepts of inequalities and intervals, which are essential for describing relationships between numbers. Inequalities compare two values, indicating whether one is greater than, less than, greater than or equal to, or less than or equal to the other. Intervals are sets of real numbers that lie between two endpoints. Understanding these concepts is crucial for representing solutions to inequalities and for describing ranges of values. Inequalities and intervals are fundamental concepts in mathematics.

Understanding Inequalities

Inequalities use symbols in below list to compare numbers.

• < (less than)
• > (greater than)
• ≤ (less than or equal to)
• ≥ (greater than or equal to)

For example, x < 5 means that x is less than 5. Solving inequalities involves finding the range of values that satisfy the condition. When multiplying or dividing both sides of an inequality by a negative number, the inequality sign must be reversed. Understanding and applying these rules is crucial for accurately solving inequalities. The proper use of inequality symbols is crucial.

Defining Intervals

Intervals are sets of real numbers between two endpoints. They can be

• Closed intervals (including the endpoints) denoted by [ a , b ]
• Open intervals (excluding the endpoints) denoted by ( a , b )
• Half-open / Half-closed (including one endpoint and excluding the other). denoted by [ a , b ) and ( a , b ]

👉 “Half-open” and “Half-closed” mean the same thing – An interval where one endpoint is included and the other is excluded.

For example, [2, 5] is a closed interval, (2, 5) is an open interval, and [2, 5) is a half-open interval. Intervals are represented graphically on a number line and are essential for describing the solutions of inequalities. Understanding intervals is essential for representing solutions. The correct use of interval notation is critical.

Solving Inequalities and Representing Solutions

Solving inequalities involves isolating the variable, similar to solving equations. However, you must pay attention to the direction of the inequality sign. For example, to solve 2x + 3 < 7, you subtract 3 from both sides, getting 2x < 4, and then divide by 2, resulting in x < 2. The solution is represented as an interval: (-∞, 2). When solving inequalities, it’s crucial to consider the direction of the inequality sign. The proper representation of solutions is essential. Solving inequalities requires careful attention to detail.

Practical Examples

Let’s look at some examples. If x > 3, the solution is represented by the interval (3, ∞). If -2x ≤ 6, dividing by -2 (and reversing the inequality sign), we get x ≥ -3, represented by the interval [-3, ∞). These examples illustrate how to solve and represent inequalities using interval notation. Understanding these concepts is essential for more advanced mathematical topics. The correct use of interval notation is critical for representing solutions.

Summary of Real Number Properties

In summary, the Real Number Properties are the foundation upon which algebra and calculus are built. We have covered closure, commutativity, associativity, the distributive law, the roles of additive and multiplicative identities, additive and multiplicative inverses, absolute value and its properties, and inequalities and intervals. Each of these properties plays a crucial role in simplifying expressions, solving equations, and understanding mathematical relationships. These properties are indispensable tools. A solid grasp of these properties is essential for success in mathematics. Understanding these properties is essential.

Review of Key Concepts

Reviewing the key concepts reinforces your understanding.

• Closure ensures that operations on real numbers result in real numbers.
• Commutativity and associativity allow for flexible rearrangement of terms.
• The distributive law links multiplication and addition.
• Additive and multiplicative identities define neutral elements.
• Additive and multiplicative inverses enable solving equations.
• Absolute value measures distance.
• Inequalities and intervals describe ranges of values.

Reviewing these key concepts consolidates your understanding. Reviewing these concepts is essential for mastery.

Practical Application

The practical application of these properties extends beyond the classroom. They are used in various fields, including engineering, physics, economics, and computer science. Understanding these properties allows you to model real-world phenomena, solve complex problems, and make informed decisions. These properties are essential tools for analyzing data, making predictions, and developing solutions. The practical applications are diverse. The application of these properties is widespread.

Key Takeaways

In conclusion, the Real Number Properties are not just a list of definitions; they are the building blocks of mathematical reasoning. By understanding and applying these properties, you can simplify complex problems, solve equations with confidence, and gain a deeper appreciation for the elegance and consistency of mathematics. Remember, practice is key. Regularly applying these properties to solve problems will strengthen your understanding and make you a more proficient mathematician. These properties are the foundation. The consistent practice will help you.

Problems and Quick Solutions

Problem 1: Simplify ##2(x + 3) – 4##

Solution: ##2x + 2##

Problem 2: Solve ##|x – 2| = 3##

Solution: ##x = 5, x = -1##

Problem 3: Verify the commutative property for ##3 × 5##

Solution: ##3 × 5 = 5 × 3 = 15##

Problem 4: Solve ##x + 5 = 12## using additive inverse

Solution: ##x = 7##

Problem 5: Simplify ##a(b – c)## using the distributive property

Solution: ##ab – ac##