Understanding the concepts of Abscissa, Ordinate & Applicate is fundamental when exploring coordinate geometry. These terms serve as the backbone of the Cartesian coordinate system, helping us pinpoint exact locations in a two-dimensional or three-dimensional space. The abscissa refers to the horizontal position of a point, while the ordinate indicates its vertical distance. Together, these values allow us to navigate the Cartesian plane with clarity. By grasping their meanings and applications, you can make sense of how various points relate to each other in design and analysis.

Moreover, let’s not overlook the role of applicate, which gives further context to a point’s projection on the axes. This concept, while often overshadowed by abscissa and ordinate, is equally important for visualizing relationships between points. As we delve deeper into these terms, you’ll see how their interplay enables complex calculations in fields like physics and engineering. Understanding the Abscissa, Ordinate & Applicate will not only enhance your mathematical skills but also enrich your comprehension of the world around you.

---

---

Definition of Abscissa and Ordinate

In a two-dimensional coordinate system, the abscissa refers to the horizontal distance of a point from the vertical axis (y-axis). For a point represented as ##(x, y)##, the abscissa is ##x##. Conversely, the ordinate defines the vertical distance of a point from the horizontal axis (x-axis), which is ##y## in the same point representation. Together, these two values uniquely determine the location of a point in a Cartesian plane.

It is crucial to visualize these terms when plotting points. For instance, the point ##(3, 4)## has an abscissa of 3 units along the x-axis and an ordinate of 4 units along the y-axis. This clear demarcation allows for precise plotting and identification of spatial relationships between various points.

Applicate in Coordinate Geometry

The term applicate, although much less commonly used than abscissa and ordinate, refers to the z-coordinate of a point in three-dimensional space. In the context of a point ##(x, y,z)##, the abscissa represents the x-value, the ordinate represents the y-value, and the applicate represents the z-value. While the term is largely historical and rarely used in modern mathematics, it provides a parallel naming structure for describing coordinates in 3D geometry.

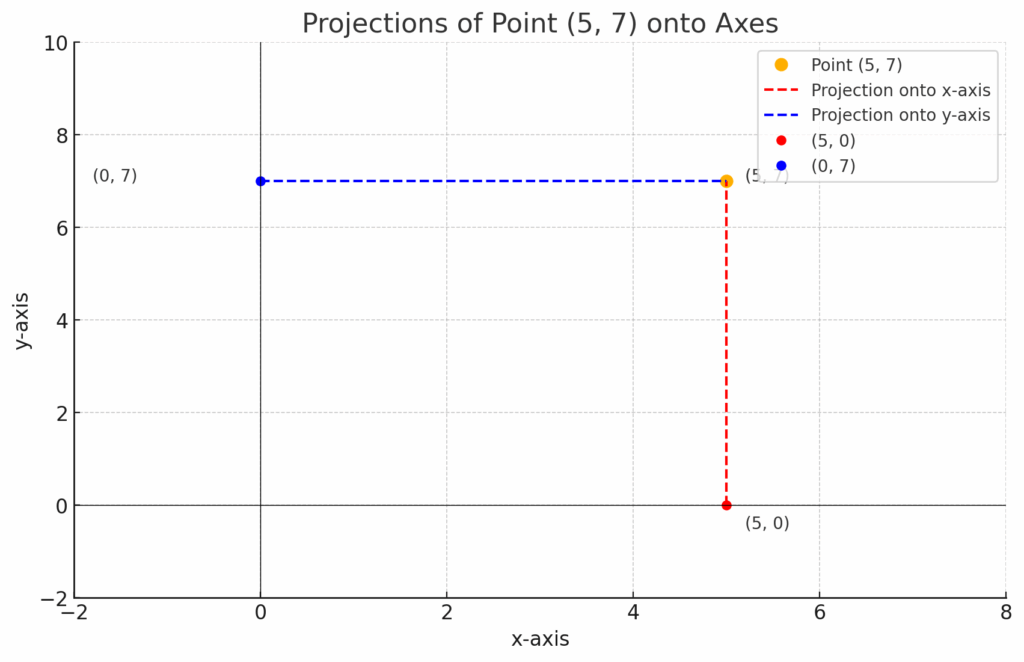
For example, consider the point ##(5,7)## in the Cartesian plane. The projection of this point onto the x-axis is ##(5,0)##, and its projection onto the y-axis is ##(0,7)## . These projections correspond to the x-component and y-component of the point, respectively. Understanding these projections is valuable for calculating distances, analyzing motion, and constructing geometric representations.

Applications of Abscissa and Ordinate

In practical applications, the concepts of abscissa and ordinate are widely employed in various fields, including physics, engineering, and computer graphics. For instance, in physics, they help in plotting trajectories by representing time as the abscissa and distance as the ordinate. Such graphical representations simplify analysis and communication of complex information.

Moreover, in computer graphics, understanding the abscissa and ordinate helps in rendering shapes, animations, and spatial arrangements. Each point plotted connects to algorithms that require accurate representations of spatial coordinates, making the comprehension of these fundamental terms essential for technology and design.

Historical Context of Coordinate System

The Cartesian coordinate system, named after the French mathematician René Descartes, revolutionized mathematics in the 17th century by linking algebra and geometry. The invention of this system allowed mathematicians to utilize algebraic equations to describe geometric shapes, marking a significant turning point in mathematics, known as analytic geometry.

The systematic use of abscissa, ordinate, and the concept of applicate subsequently arose, enabling mathematicians to communicate spatial data in a more structured, understandable way. This fusion of concepts has laid the groundwork for further advancements in calculus and modern physics, establishing a solid foundation we continue to build upon today.

Examples of Abscissa, Ordinate, and Applicate

Example 1: Point Location

Consider the point ##(2, 3)##. Here, the abscissa is ##2## and the ordinate is ##3##. The applicate concerning the x-axis is ##(2, 0)##, and concerning the y-axis is ##(0, 3)##. This clearly shows how these elements relate to one another in a geometric context.

Example 2: Graphing a Function

Let’s graph the linear function ##y = 2x + 1##. The abscissa values (x-values) significantly influence the ordinate values (y-values). By choosing different values for x such as ##0, 1, 2##, we find corresponding y-values of ##1, 3, 5##, respectively, exemplifying how changes in the abscissa impact the ordinate when plotting on the graph.

Final Summary

In conclusion, the concepts of abscissa, ordinate, and applicate are pivotal in understanding coordinate geometry. They provide a robust framework for describing points’ locations and transforming complex geometrical phenomena into analytical relationships. Mastering these terms is essential for anyone wishing to delve deeper into the realms of mathematics, physics, and technical disciplines.

Additional Problems Related to Abscissa and Ordinate

Problem 1: Find the abscissa and ordinate of the point ##(-4, 5)##.

Abscissa is ##-4##; ordinate is ##5##.

Problem 2: What are the coordinates of the applicate from the point ##(6, -2)## to the x-axis?

The applicate is the point ##(6, 0)##.

Problem 3: Plot the point ##(1, 1)## and identify the abscissa and ordinate.

Abscissa is ##1##; ordinate is ##1##.

Problem 4: What is the ordinate of the point ##(-3, 7)##?

The ordinate is ##7##.

Problem 5: Determine the applicate of point ##(4, -5)## on the y-axis.

The applicate on the y-axis is the point ##(0, -5)##.

---

---