Welcome! This chapter will explore how we can manipulate geometric shapes and figures in the coordinate plane. We’ll cover four primary types of transformations: translation, rotation, reflection, and dilation. Understanding these transformations is fundamental to many areas of mathematics and physics, providing a powerful tool for analyzing and manipulating geometric objects. The principles of Transformations in Coordinate Geometry are used in computer graphics, robotics, and various engineering applications.

Each transformation has a unique set of rules that alter the position, size, or orientation of a geometric figure. These transformations are not just theoretical concepts; they have practical applications in fields like computer graphics and robotics. Furthermore, we will learn how to apply these rules to specific points and figures, and how to visualize the results.

---

---

Understanding Transformations

Transformations in coordinate geometry involve changing the position, size, or orientation of a geometric figure. These changes are achieved by applying specific rules or operations to the coordinates of the points that make up the figure. Each type of transformation has a unique set of rules, and by applying these rules, we can move, rotate, reflect, or resize shapes in the coordinate plane. The key idea is to map each point of the original figure (the pre-image) to a new point (the image) based on a defined transformation rule. This process is fundamental to understanding how shapes relate to each other.

The study of transformations also helps us understand the concept of congruence (same shape and size) and similarity (same shape, different size). Transformations are often represented using matrices, which provide a concise and elegant way to describe the transformation rules. For instance, a 2×2 matrix can represent a rotation or a scaling transformation. By multiplying the coordinate vector of a point by the transformation matrix, we obtain the coordinates of the transformed point. This matrix representation is especially useful in computer graphics and other applications where multiple transformations need to be applied sequentially.

Types of Transformations

Translation

Translation involves shifting a figure along a straight line without changing its size or orientation. Think of it as sliding the figure across the plane.

To translate a point ##(x, y)## by a vector ##(h, k)##, we add ##h## to the x-coordinate and ##k## to the y-coordinate. The new coordinates of the translated point are ##(x + h, y + k)##.

This transformation is straightforward and preserves the shape and size of the original figure, making it a fundamental concept in understanding how objects can be repositioned in space.

For example, if we translate the point ##(2, 3)## by the vector ##(1, -2)##, the new coordinates will be ##(2 + 1, 3 – 2) = (3, 1)##. Consider a triangle with vertices A(1,1), B(3,1), and C(2,3). If we translate this triangle by the vector (2,1), the new vertices will be A'(3,2), B'(5,2), and C'(4,4). This demonstrates how each point of the figure is moved by the same amount in the same direction. This type of transformation is widely used in various fields, including computer graphics and game development, to move objects on the screen.

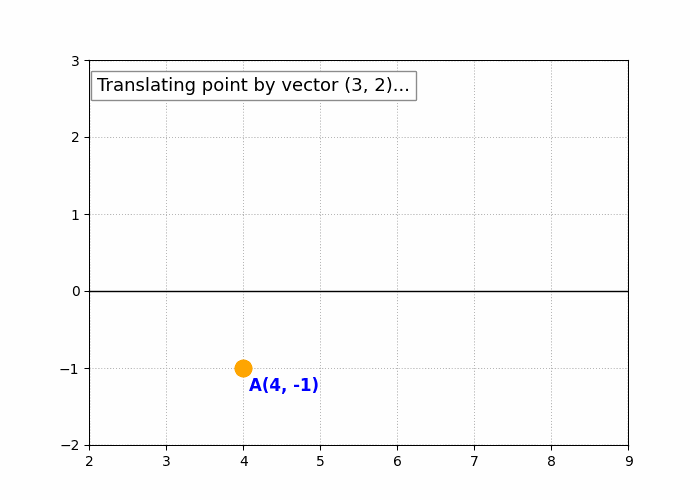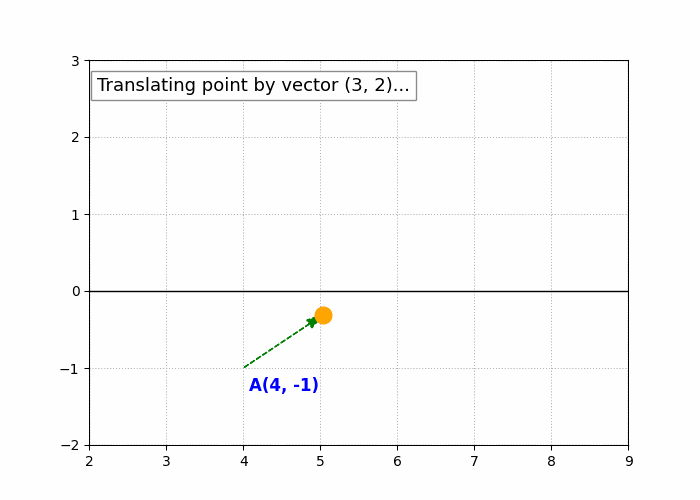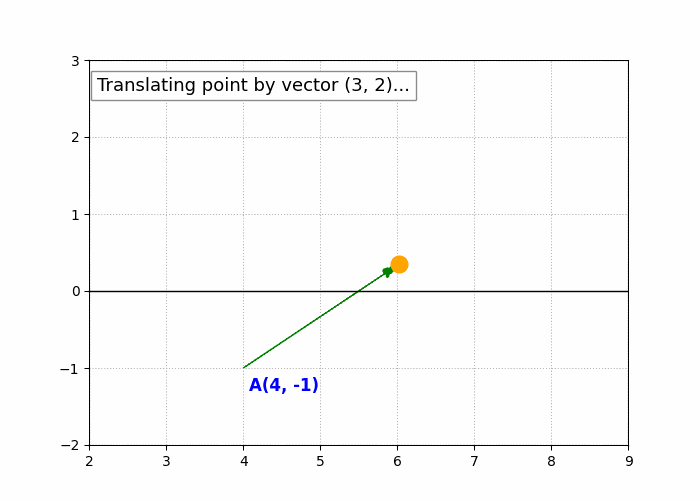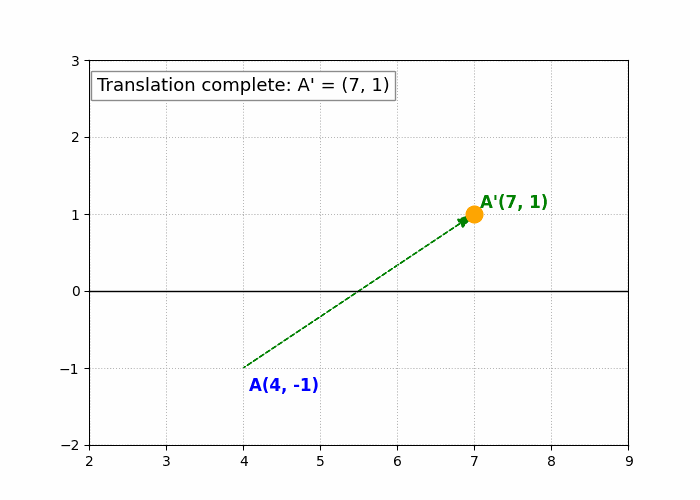
Example: Translate the point ##(4, -1)## by ##(3, 2)##.

Solution: ##(4 + 3, -1 + 2) = (7, 1)##

Rotation

Rotation involves turning a figure around a fixed point, called the center of rotation. The rotation is specified by an angle and a direction (clockwise or counterclockwise). The most common center of rotation is the origin ##(0, 0)##. The formulas for rotating a point ##(x, y)## counterclockwise by an angle ##\theta## about the origin are:

### x' = x \cos(\theta) – y \sin(\theta) ### ### y' = x \sin(\theta) + y \cos(\theta) ###

These formulas are derived from trigonometric principles and ensure that the distance from the center of rotation to each point remains constant. Rotation is a fundamental concept in geometry, and it is used extensively in various applications, such as computer graphics and physics.

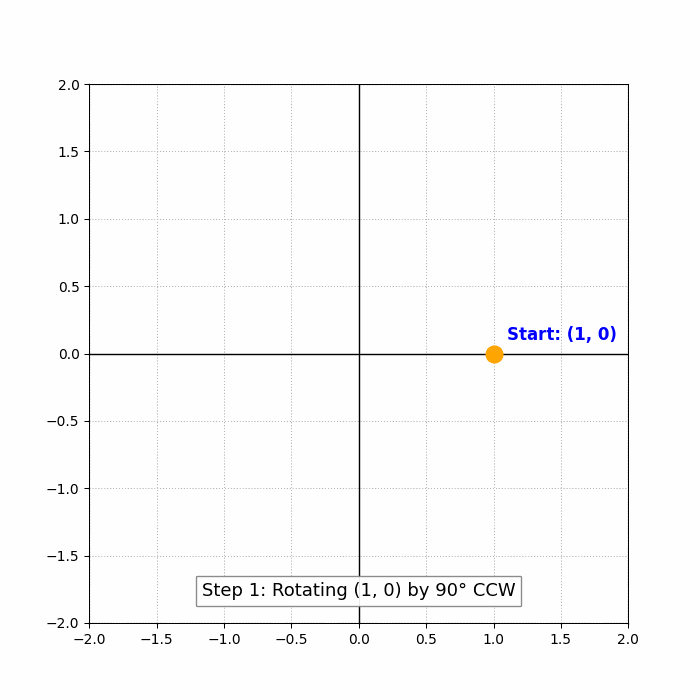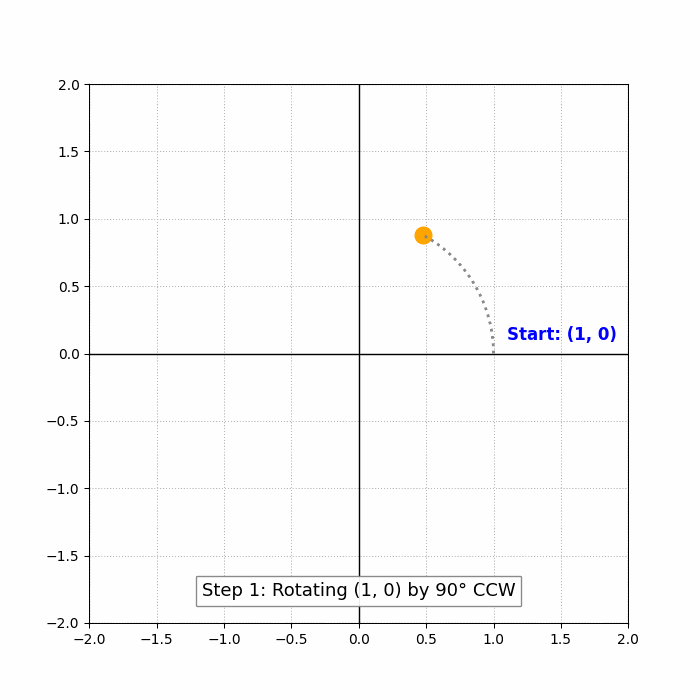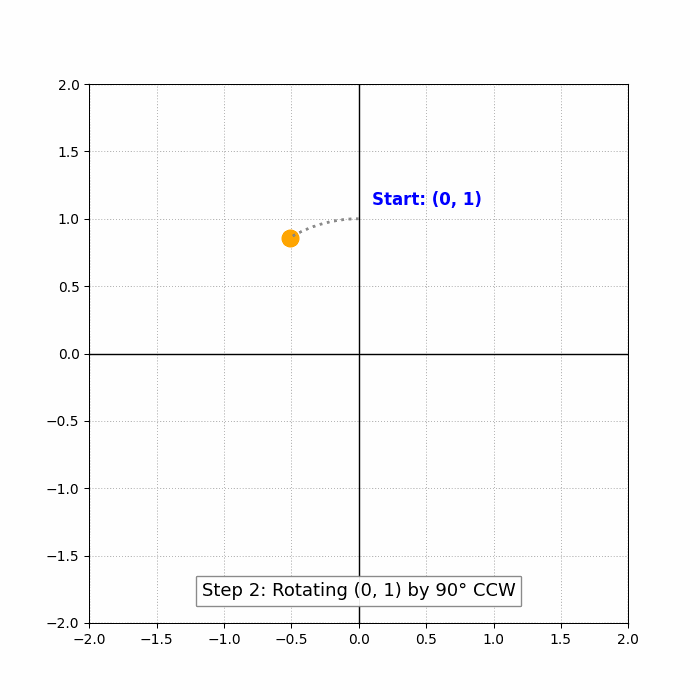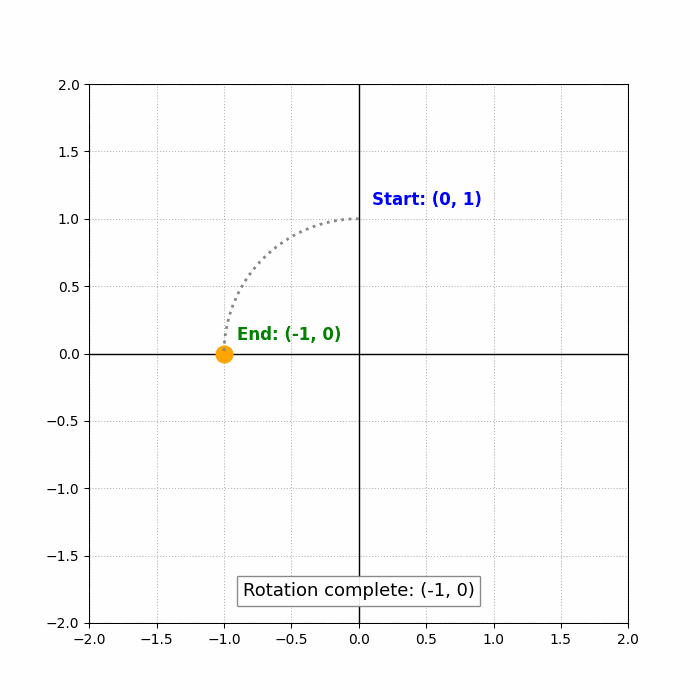
Step 1: Rotating the point (1,0) by 90 degrees counterclockwise

If we rotate the point (1,0) by 90 degrees counterclockwise, then ##\theta = 90^\circ##, and we use the formulas:

### x' = 1 \cos(90^\circ) – 0 \sin(90^\circ) = 1 \cdot 0 – 0 \cdot 1 = 0 ### ### y' = 1 \sin(90^\circ) + 0 \cos(90^\circ) = 1 \cdot 1 + 0 \cdot 0 = 1 ###

So the point (1,0) becomes (0,1).

Step 2: Rotating the point (0,1) by 90 degrees counterclockwise

If we rotate the point (0,1) by 90 degrees counterclockwise, then ##\theta = 90^\circ##, and we use the formulas:

### x' = 0 \cos(90^\circ) – 1 \sin(90^\circ) = 0 \cdot 0 – 1 \cdot 1 = -1 ### ### y' = 0 \sin(90^\circ) + 1 \cos(90^\circ) = 0 \cdot 1 + 1 \cdot 0 = 0 ###

So the point (0,1) becomes (-1,0).

Example: Rotate the point ##(2, 2)## by 180 degrees counterclockwise about the origin.

Solution: ##x’ = 2 \cos(180^\circ) – 2 \sin(180^\circ) = -2##, ##y’ = 2 \sin(180^\circ) + 2 \cos(180^\circ) = -2##. The new point is ##(-2, -2)##

Reflection

Reflection involves flipping a figure over a line, called the line of reflection (or mirror). The line of reflection acts as a mirror, and the image is the same distance from the line as the original figure, but on the opposite side. Common lines of reflection include the x-axis, the y-axis, and the line ##y = x##. Reflecting a point ##(x, y)## over the x-axis results in the point ##(x, -y)##. Reflecting over the y-axis results in the point ##(-x, y)##. Reflecting over the line ##y = x## results in the point ##(y, x)##. These transformations are essential for understanding symmetry and geometric properties.

For instance, reflecting the point ##(3, 2)## over the x-axis gives us ##(3, -2)##, while reflecting it over the y-axis gives us ##(-3, 2)##. Reflecting the point (5, 1) over the line y = x gives (1, 5). The distance from the original point to the line of reflection is the same as the distance from the reflected point to the line. This property is fundamental to the concept of reflection and symmetry. Reflection is widely used in art, design, and architecture to create symmetrical patterns and structures.

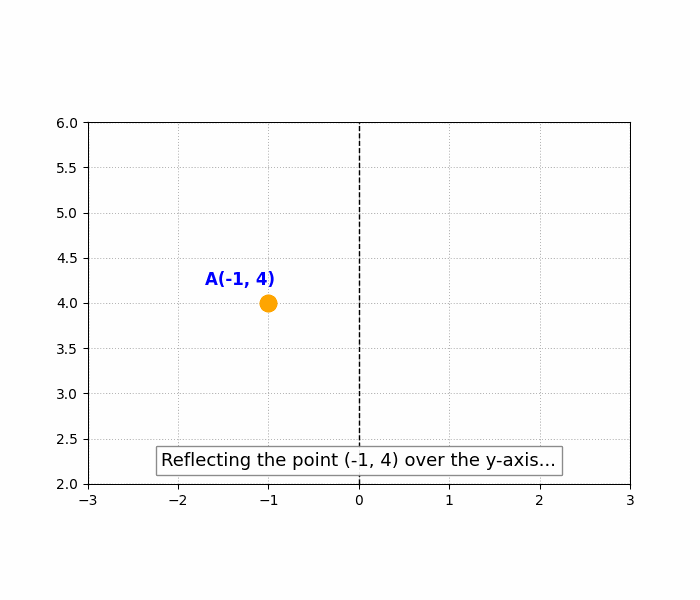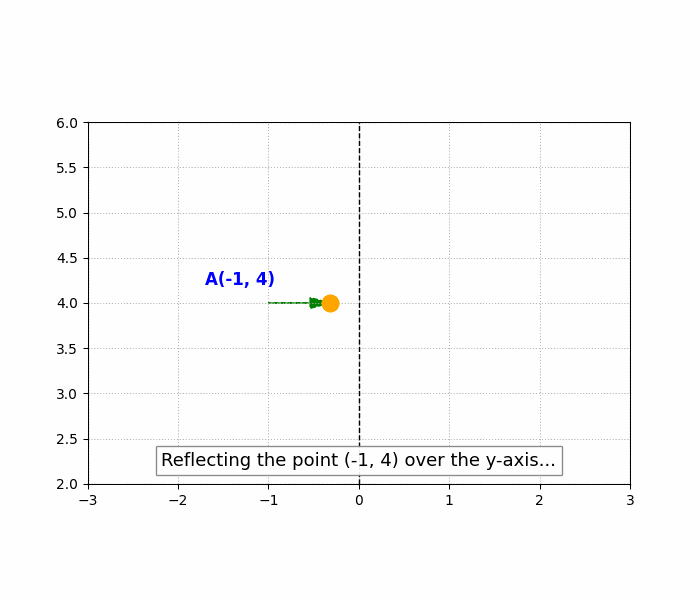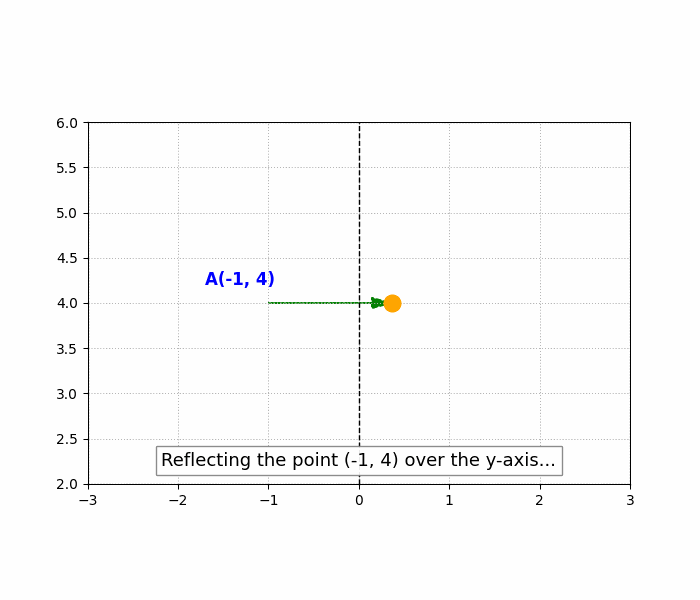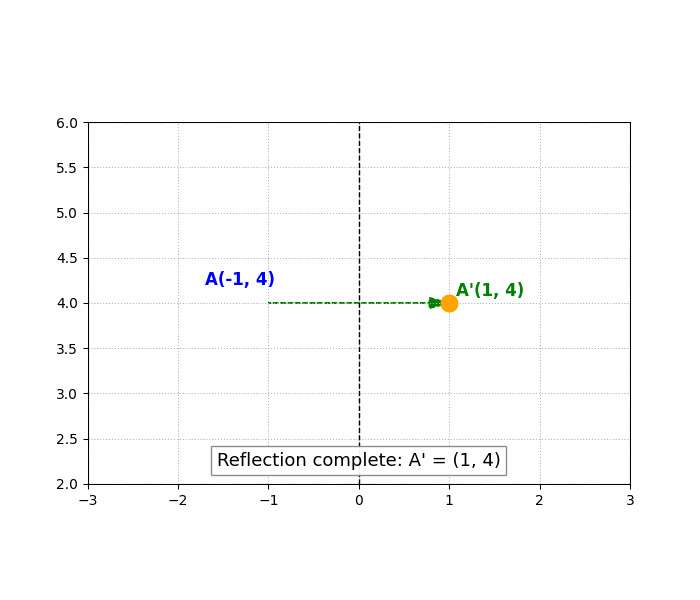
Example: Reflect the point ##(-1, 4)## over the y-axis.

Solution: ##(-(-1), 4) = (1, 4)##

Dilation

Dilation involves resizing a figure by a scale factor. The figure is either enlarged or reduced, depending on the scale factor. The dilation is performed with respect to a center of dilation, which is typically the origin ##(0, 0)##. If the scale factor is ##k##, then the coordinates of the point ##(x, y)## are multiplied by ##k##, resulting in the point ##(kx, ky)##. If ##k > 1##, the figure is enlarged; if ##0 < k < 1##, the figure is reduced; and if ##k < 0##, the figure is reflected and scaled. Dilation is a fundamental concept in understanding similarity and scaling in geometry.

For example, dilating the point ##(2, 3)## by a scale factor of 2 results in the point ##(4, 6)##. Dilating the point (4, 6) by a scale factor of 0.5 results in the point (2, 3). If the scale factor is negative, the figure is reflected across the origin and scaled. For instance, dilating the point (1, 1) by a scale factor of -2 results in the point (-2, -2). This concept is widely used in various fields, including computer graphics and image processing, to resize and manipulate images.

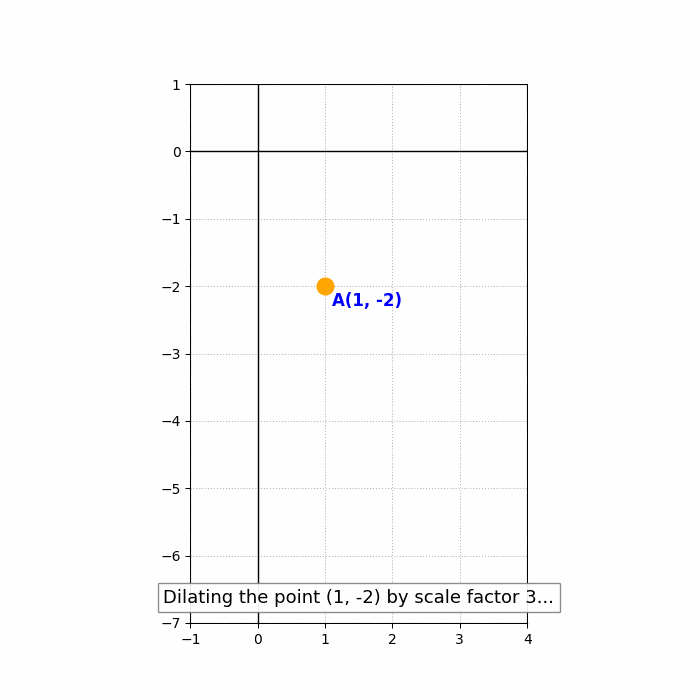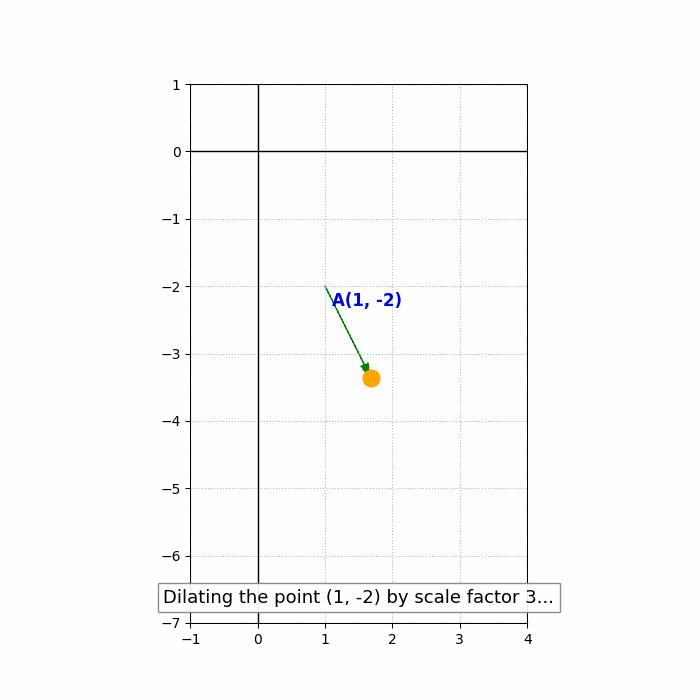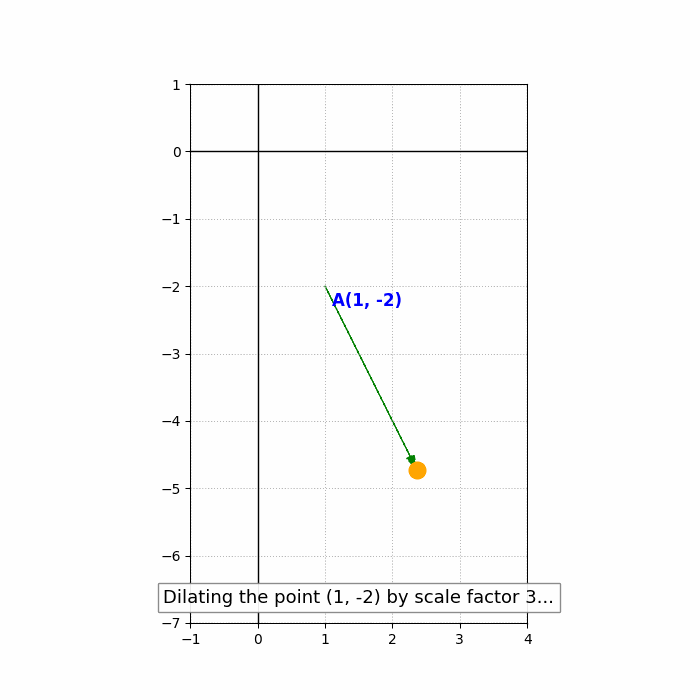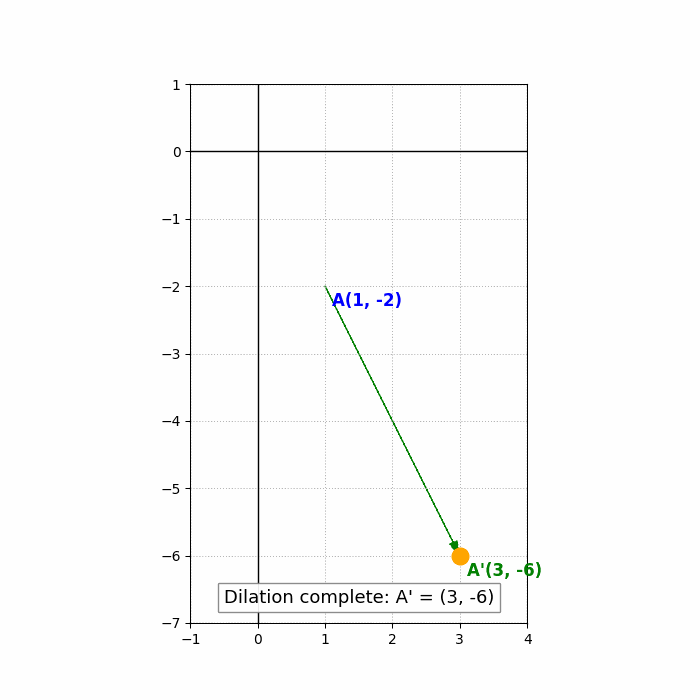
Example: Dilate the point ##(1, -2)## by a scale factor of 3.

Solution: ##(1 \cdot 3, -2 \cdot 3) = (3, -6)##

Additional Problems

Problem 1: Translate the point (5, -2) by the vector (-1, 4).

Solution: (4, 2)

Problem 2: Rotate the point (3, 0) by 90 degrees clockwise about the origin.

Solution: (0, -3)

Problem 3: Reflect the point (-2, 1) over the x-axis.

Solution: (-2, -1)

Problem 4: Dilate the point (4, 6) by a scale factor of 0.5.

Solution: (2, 3)

Problem 5: Reflect the point (1, 2) over the line y = x.

Solution: (2, 1)

---

---