The additive inverse of a number is what you add to that number to get a sum of zero. For any given number, its additive inverse is the opposite of that number on the number line.
The additive inverse of an element is a fundamental concept in mathematics that plays a crucial role in various mathematical operations and theories. This concept is not only essential in arithmetic but also in algebra and other advanced mathematical studies.
What is the Additive Inverse?
In mathematics, the additive inverse of a number is the number that, when added to the original number, yields a sum of zero. The general formula to find the additive inverse of any number a is -a. This means that if you have a positive number, its additive inverse will be negative, and vice versa.
“Mathematics is not about numbers, equations, computations, or algorithms: it is about understanding.” — William Paul Thurston
Finding the Additive Inverse
Finding the additive inverse is a straightforward process. For any real number, the additive inverse can be determined by changing the sign of the number. For example:
# Finding the additive inverse of a positive number
a = 5
additive_inverse = -a
print(additive_inverse)
-5
In this example, the additive inverse of 5 is -5. Similarly, the additive inverse of -7 is 7:
# Finding the additive inverse of a negative number
a = -7
additive_inverse = -a
print(additive_inverse)
7
We also Published
- From Kaṇāda to Rutherford: Tracing the Evolution of Atomic Theory
The evolution of atomic theory is a long and winding road that has been travelled by some of the greatest minds in history. It began with the ancient Indians in 600 BC who gave the concept of "Parmanu" to Greeks who first proposed that matter was made up of tiny, indivisible particles. The 19th and 20th centuries saw significant advances in our understanding of atoms. - Tuples
In mathematics, a tuple or a sequence is a list of objects arranged in an order. Such a list may have repeated objects but the order is more important. Such sequences or tuples are denoted as ( t1, t2, t3, …., tn ) where tn is the nth element of the list. Below are a few examples of tuples. (x, […] - The Pivotal Role of Supernova Explosions in Shaping Our Universe
Supernova explosions: cosmic catalysts that seed the universe with heavy elements, shaping the very fabric of our existence.
The Importance of Additive Inverses
Understanding the concept of additive inverses is crucial because it lays the foundation for more advanced mathematical concepts, such as solving equations. In algebra, the ability to isolate a variable often relies on using the additive inverse to cancel out terms on one side of an equation.
For instance, consider the equation x + 3 = 7. To solve for x, you need to subtract 3 from both sides of the equation. Here, subtracting 3 is equivalent to adding the additive inverse of 3, which is -3:
#Solving an equation using additive inverse
x = 7 - 3
print(x)
4
Thus, understanding how to apply the additive inverse can simplify the process of solving various types of equations.
The Additive Inverse in Algebraic Structures
In mathematics, the additive inverse of an element \( x \), denoted as \(-x\), is the element that, when added to \( x \), yields the additive identity, which is \( 0 \). Typically, this identity is the number 0, though in various contexts, it may be a more generalized zero element. In elementary mathematics, we commonly refer to the additive inverse as the opposite number. This concept is closely related to subtraction and is crucial for solving algebraic equations. However, not all sets where addition is defined possess an additive inverse, such as the natural numbers.
For integers, rational, real, and complex numbers, finding the additive inverse is straightforward: simply multiply the number by \(-1\).. Moreover, this concept extends to algebraic expressions, proving essential for balancing equations. Historically, the dual role of the minus sign in both subtraction and indicating opposites led to the development of the additive inverse concept.
The use of the minus sign for both subtraction and indicating opposite magnitudes dates back to the 17th century, though it initially faced resistance from some mathematicians who feared it could cause confusion.
In an algebraic structure defined by addition \((S, +)\) with an additive identity \( e \in S \), an element \( x \in S \) has an additive inverse \( y \in S \) if and only if \( x + y = e \) and \( y + x = e \). While addition is generally considered a commutative operation, it is not necessarily associative. When associativity holds, meaning \((a + b) + c = a + (b + c)\), the left and right inverses will align, making the additive inverse unique. However, in non-associative cases, left and right inverses may differ, leading to situations where an inverse does not exist. The definition also requires closure, meaning the additive inverse \( y \) must be within the set \( S \). This is why natural numbers do not have an additive inverse within their set, whereas integers do, with their inverses being the negative numbers.
Additive Inverse in Vector Spaces
The additive inverse concept extends beyond real numbers to encompass vectors within vector spaces. For any vector v, the additive inverse is a vector -v such that v + (-v) = 0, where 0 is the zero vector.
Physicists and engineers find this property especially useful, as vectors represent quantities such as force and velocity. The additive inverse enables the analysis of opposing directions and the balancing of forces in equilibrium conditions.
The additive inverse serves as a foundational concept in mathematical operations. Whether working with simple numbers, intricate algebraic equations, or vector spaces, a grasp of the additive inverse proves essential for problem-solving and mathematical progression. Mastering this concept provides a deeper understanding of mathematical structure and its practical applications.
Examples of Additive Inverses in Arithmetic
Example 1:
Number: 5
Additive Inverse: -5
Verification: 5 + (-5) = 0
Example 2:
Number: -8
Additive Inverse: 8
Verification: -8 + 8 = 0
Example 3:
Number: 12
Additive Inverse: -12
Verification: 12 + (-12) = 0
Example 4:
Number: -3
Additive Inverse: 3
Verification: -3 + 3 = 0
Example 5:
Number: 0
Additive Inverse: 0
Verification: 0 + 0 = 0
Examples of Additive Inverses in Geometry
Example 1: Point on a Number Line
Point: 7 units to the right of the origin (7)
Additive Inverse: 7 units to the left of the origin (-7)
Verification: The points are symmetric about the origin, and 7 + (-7) = 0.

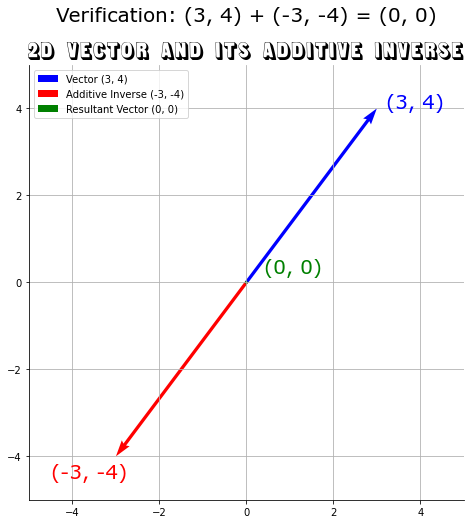
Example 2: 2D Vector
Vector: (3, 4)
Additive Inverse: (-3, -4)
Verification: Adding the vectors (3, 4) and (-3, -4) gives (0, 0).
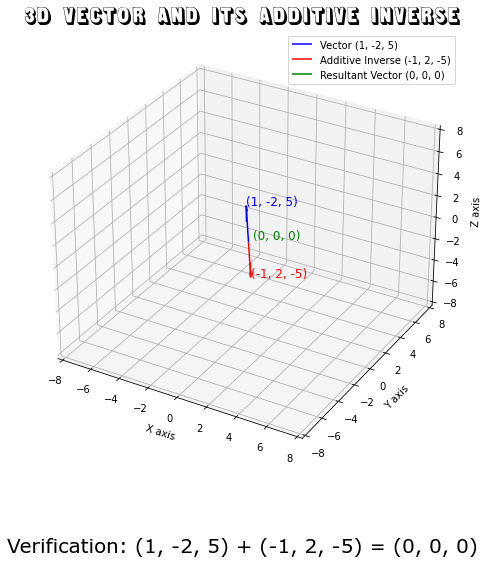
Example 3: 3D Vector
Vector: (1, -2, 5)
Additive Inverse: (-1, 2, -5)
Verification: Adding the vectors (1, -2, 5) and (-1, 2, -5) results in (0, 0, 0).
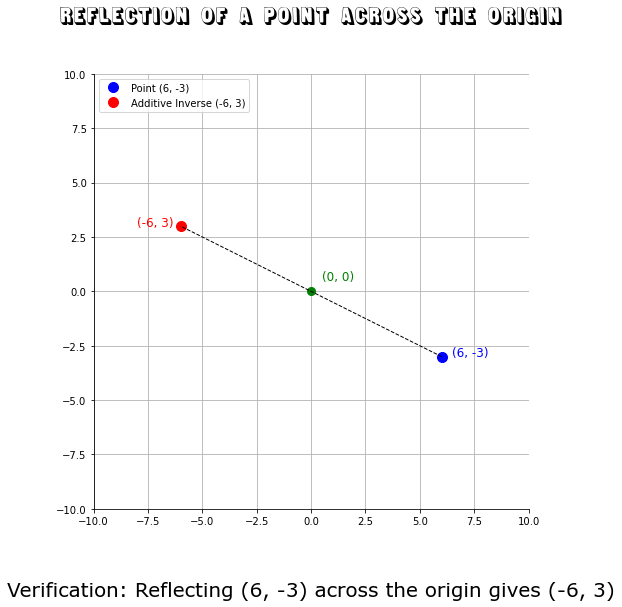
Example 4: Coordinate Point Reflection in 2D
Point: (x, y) = (6, -3)
Additive Inverse: (-x, -y) = (-6, 3)
Verification: Reflecting the point (6, -3) across the origin gives (-6, 3).
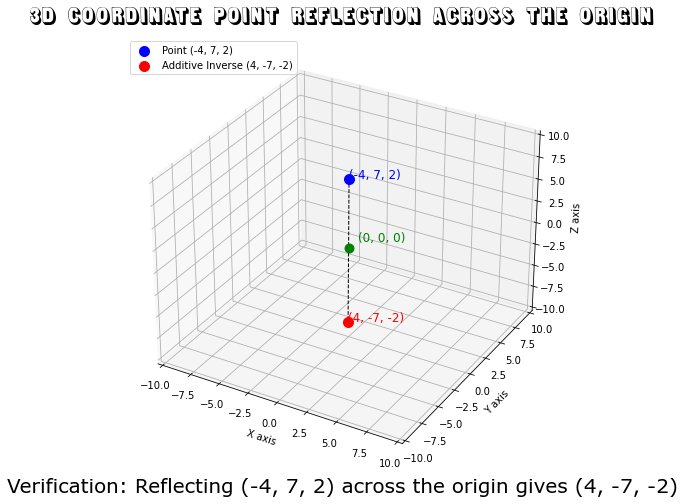
Example 5: Coordinate Point Reflection in 3D
Point: (x, y, z) = (-4, 7, 2)
Additive Inverse: (-x, -y, -z) = (4, -7, -2)
Verification: Reflecting the point (-4, 7, 2) across the origin gives (4, -7, -2).
RESOURCES
- What is the additive inverse of -7?
- real analysis - Proving an Additive Inverse - Mathematics Stack Exchange
- Real Analysis: I
- Additive Inverse
- Just a moment...
- Find the additive inverse of 10\\[\\begin{align} \\text{a) 0} \\\\ \\text{b) -10} \\\\ \\text{c) 8} \\\\ \\text{d) None of these} \\\\ \\end{align}\\]
- Additive Inverse -- from Wolfram MathWorld
- Additive Inverse - Property, Definition, Formula, Examples
- What is the additive inverse of any element in the group? Is it commutative or associative? - Quora







0 Comments