ADVERTISEMENT
As θ → 0, we have cosθ → 1
Proof :
When θ = 0, We have, lim\(_{θ\to 0} \cos \)θ = cos0 = 1 { ∵ cos0 = 1 }
Hence,
Discover the world of synthetic morphogenesis. Learn how scientists program multicellularity to create functional tissues, organoids, and living sensors using genetic circuits.
The Human Pangenome Reference marks a shift from linear genomes to graph-based diversity. Discover how T2T sequencing and structural variation are transforming precision medicine.
Explore the shift from static AlphaFold predictions to real-time protein dynamics. Learn how cryo-ET and AI are visualizing molecular motion for drug discovery and personalized medicine.
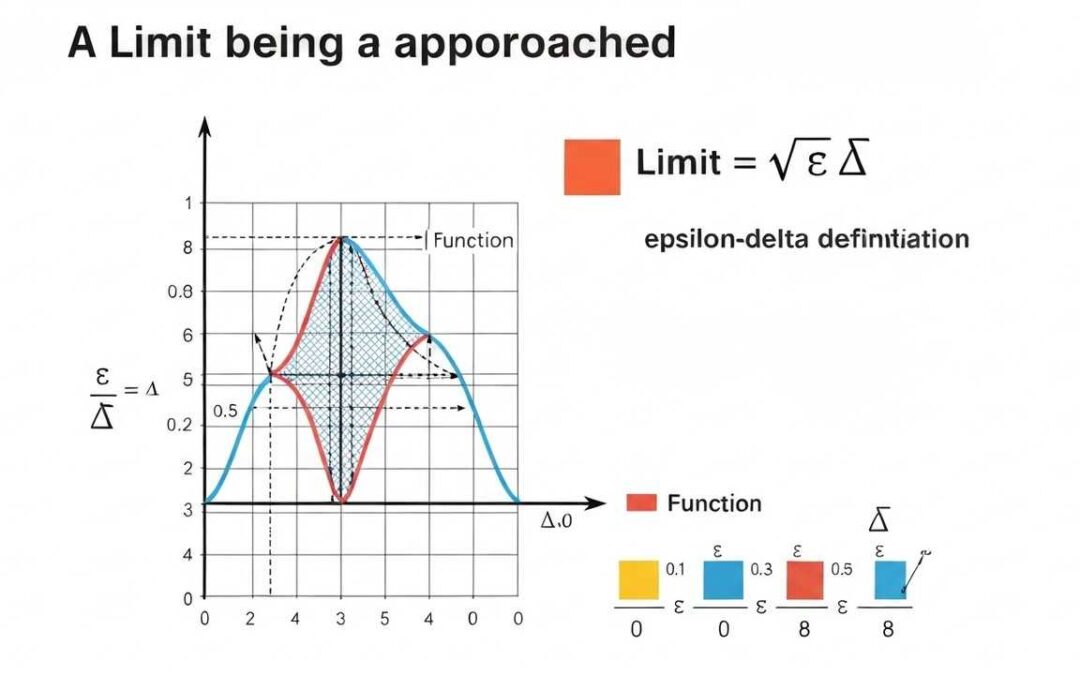
Understanding **limits of functions** is essential in calculus. This guide explains the epsilon-delta definition, theorems, and applications to help you master this fundamental concept.
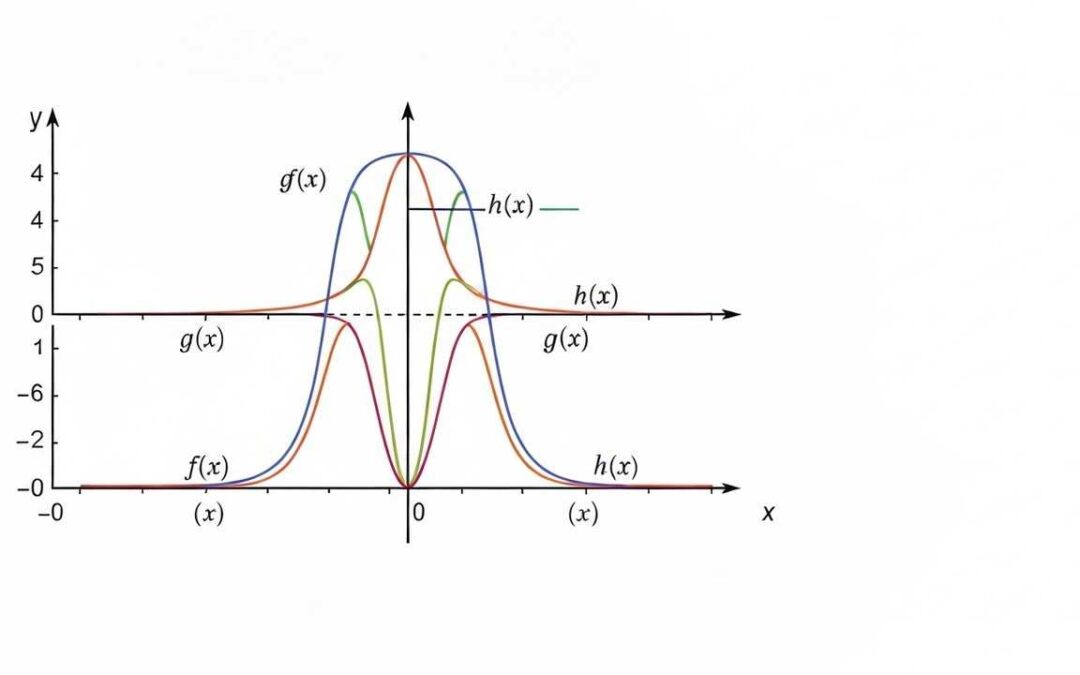
The Squeeze Theorem is a calculus concept that uses bounding functions to determine the limit of a function. The article explains how it works and provides examples.
Learn how to solve Evaluating Limits Problems with this step-by-step guide. We’ll cover the fundamentals and provide clear examples.
Learn how to solve Limits at Infinity with this comprehensive guide. Understand the concepts and techniques through clear examples and step-by-step solutions.
0 Comments