Limits are a fundamental concept in calculus, and understanding them is essential for anyone venturing into the world of higher mathematics. Limits of functions provide the foundation for understanding continuity, derivatives, and integrals, which are core to the subject. This article will explore the core concepts of limits, providing a clear and accessible guide to this crucial mathematical idea.
Table of Contents
- Delving into the Definition of a Limit
- The Epsilon-Delta Definition
- Understanding the Components
- Visualizing the Concept
- Limit Superior and Limit Inferior
- Essential Limit Theorems and Properties
- Common Limits of Elementary Functions
- Advanced Techniques: L’Hôpital’s Rule and Beyond
- Key Takeaways
- Similar Problems (Quick Solutions)
Read More
Limits form the bedrock of calculus, essential for understanding continuity, derivatives, and integrals. The concept involves examining the behavior of a function as its input approaches a specific value. This guide delves into the fundamental definitions, theorems, and applications of limits, equipping you with the knowledge to tackle complex calculus problems. Let’s explore the core principles that make limits a cornerstone of mathematical analysis.
Delving into the Definition of a Limit
What exactly defines a limit? It’s not just a concept, but a precise mathematical statement. It’s a formal way of expressing the idea that a function ‘approaches’ a certain value as the input gets arbitrarily close to a specific point. The formal definition, often called the epsilon-delta definition, provides a rigorous framework for understanding this concept. This framework is crucial for proving theorems and ensuring the logical consistency of calculus.
The Epsilon-Delta Definition
The epsilon-delta definition states that for a function ##f(x)##, the limit as ##x## approaches ##c## equals ##L## if, for every ##ε > 0##, there exists a ##δ > 0## such that if ##0 < |x – c| < δ##, then ##|f(x) – L| < ε##. This means that no matter how small we make ##ε##, we can always find a ##δ## that ensures ##f(x)## is within ##ε## of ##L## whenever ##x## is within ##δ## of ##c##. The epsilon-delta definition is fundamental in establishing the rigorous foundation of calculus.
Understanding the Components
Breaking down the definition, ##ε## represents the desired accuracy or tolerance, and ##δ## represents the proximity to ##c##. The condition ##0 < |x – c| < δ## signifies that ##x## is close to ##c## but not equal to ##c##. The inequality ##|f(x) – L| < ε## ensures that the function’s value, ##f(x)##, is close to the limit ##L##. This precise language ensures a clear understanding of the behavior of functions near a specific point.
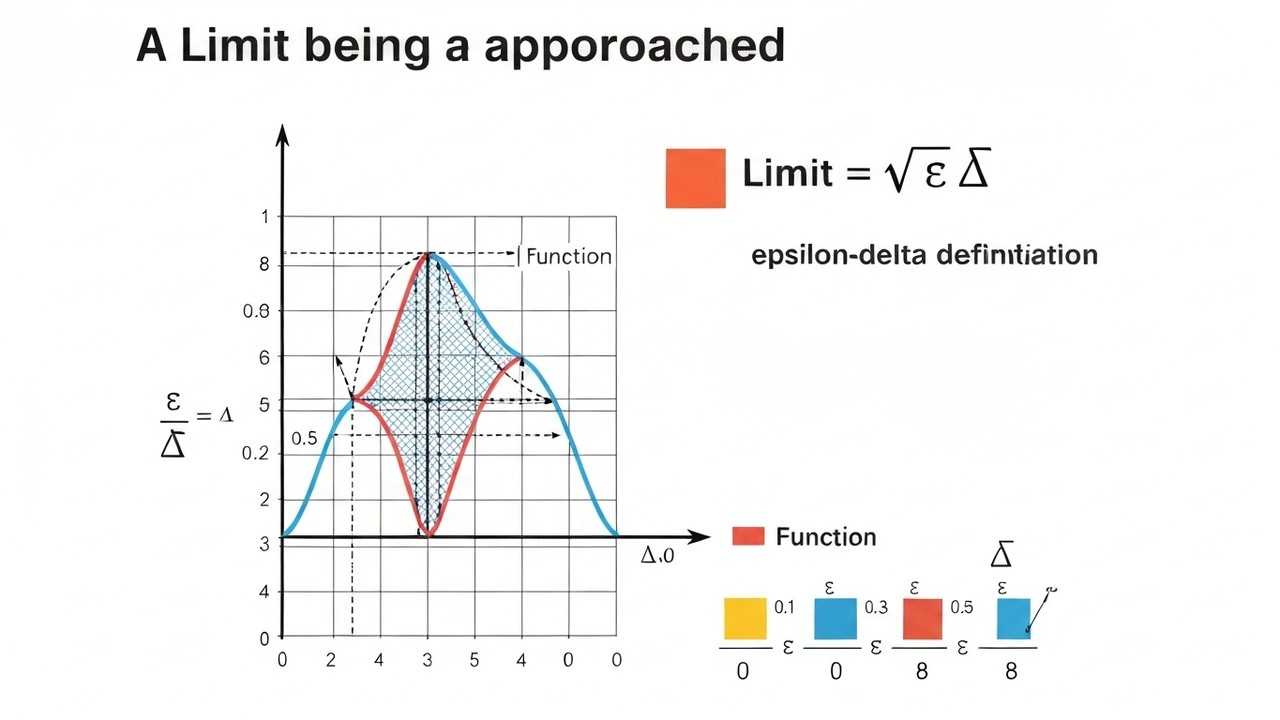
Visualizing the Concept
Imagine a graph of a function. The limit ##L## is the value that the function approaches as ##x## gets closer to ##c##. The ##ε## value defines a horizontal band around ##L##, and the ##δ## value defines a vertical band around ##c##. If the function stays within the horizontal band whenever ##x## is within the vertical band, the limit exists. This visual aid is helpful for understanding the definition.
Limit Superior and Limit Inferior
Besides the basic limit, there are related concepts like the limit superior and limit inferior. These are especially useful when a limit does not exist. The limit superior, denoted as ##lim sup##, represents the largest value that the sequence can get arbitrarily close to. The limit inferior, denoted as ##lim inf##, represents the smallest such value. These concepts are important for sequences that do not converge to a single value.
Essential Limit Theorems and Properties
Several theorems simplify limit calculations and provide a toolkit for working with limits. These theorems allow us to evaluate limits of complex functions by breaking them down into simpler components. These theorems are essential for developing proficiency in calculus and understanding the behavior of functions. They provide a framework for manipulating limits, making complex problems more manageable.
Limit Laws
The limit laws dictate how limits interact with algebraic operations. For instance, the limit of a sum is the sum of the limits, and the limit of a product is the product of the limits, provided the individual limits exist. These laws are fundamental for simplifying limit calculations. They apply to addition, subtraction, multiplication, division, and powers. They streamline the process of evaluating limits.
Continuity and Limits
A function is continuous at a point ##c## if the limit of the function as ##x## approaches ##c## exists, is equal to the function’s value at ##c##, and the function is defined at ##c##. This means the function has no breaks or jumps at that point. Continuity is closely tied to limits, and it ensures that small changes in the input result in small changes in the output. This property is critical in many areas of calculus.
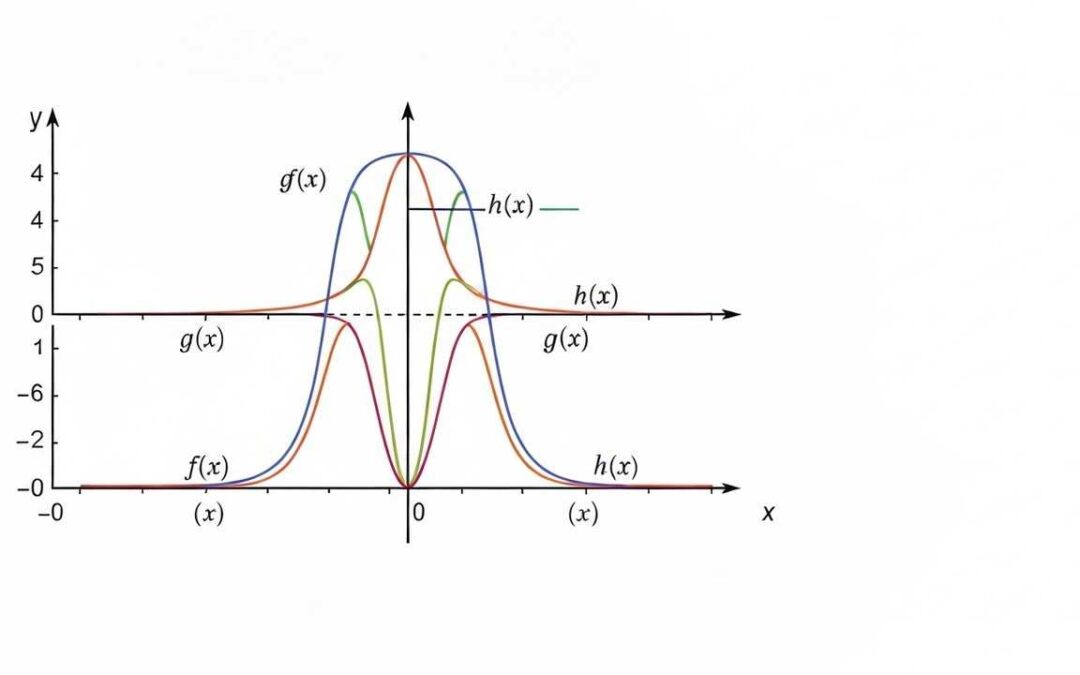
Squeeze Theorem
The squeeze theorem, also known as the sandwich theorem, states that if a function ##g(x)## is squeezed between two functions, ##f(x)## and ##h(x)##, and ##f(x)## and ##h(x)## both approach the same limit ##L## as ##x## approaches ##c##, then ##g(x)## also approaches ##L##. This theorem is useful for finding limits of functions that are difficult to evaluate directly. It’s a valuable tool for situations where direct calculation is not feasible.
Common Limits of Elementary Functions
Certain limits frequently appear in calculus problems, especially those involving elementary functions. These include polynomials, rational functions, exponential functions, logarithmic functions, trigonometric functions, and their inverses. Knowing these standard limits streamlines problem-solving and builds intuition. Mastering these is a key step in becoming proficient in calculus. They are the building blocks for more complex calculations.
Polynomials and Rational Functions
For a polynomial function, the limit as ##x## approaches ##c## is simply the value of the polynomial at ##c##. Rational functions, which are ratios of polynomials, follow this rule at points where the denominator is not zero. For example, ##lim_{x \to c} (ax + b) = ac + b##, which is a direct application of the limit laws and the definition of continuity. These limits are straightforward to calculate.
Exponential and Logarithmic Functions
The exponential function ##e^x## is continuous everywhere, so ##lim_{x \to c} e^x = e^c##. Logarithmic functions, such as ##ln(x)##, are also continuous on their domain, so ##lim_{x \to c} ln(x) = ln(c)##, provided ##c > 0##. These properties are crucial for analyzing growth and decay. They are essential in many applications.
Trigonometric Functions
Trigonometric functions also have standard limits. For instance, ##lim_{x \to 0} \frac{sin(x)}{x} = 1##, a fundamental result used in many trigonometric calculations. Additionally, ##lim_{x \to 0} \frac{1 – cos(x)}{x} = 0##. These limits are vital for understanding periodic phenomena. They are key to working with oscillatory behavior.
Advanced Techniques: L’Hôpital’s Rule and Beyond
When direct application of limit laws fails, advanced techniques like L’Hôpital’s rule provide powerful tools for evaluating limits. These techniques are used when the limit results in an indeterminate form, such as ##0/0## or ##\infty/\infty##. They involve using derivatives to simplify the limit expression. These techniques extend the range of problems that can be solved.
L’Hôpital’s Rule
L’Hôpital’s rule states that if the limit of ##\frac{f(x)}{g(x)}## results in an indeterminate form, then ##lim_{x \to c} \frac{f(x)}{g(x)} = lim_{x \to c} \frac{f'(x)}{g'(x)}##, provided the limit on the right-hand side exists. This rule simplifies limits that would otherwise be difficult to compute. It involves differentiating the numerator and denominator separately. L’Hôpital’s rule is a cornerstone of advanced limit calculations.
Other Techniques
Besides L’Hôpital’s rule, other techniques include algebraic manipulation, trigonometric identities, and series expansions. For example, factoring, rationalizing denominators, or applying trigonometric identities can transform a limit into a more manageable form. Using Taylor series can also help when dealing with complex functions. These methods are crucial for handling a diverse range of limit problems.
Key Takeaways
Understanding limits is fundamental to calculus and the broader field of mathematics. The epsilon-delta definition provides a rigorous framework, while limit theorems and properties simplify calculations. Knowing the limits of elementary functions and applying advanced techniques like L’Hôpital’s rule expands your problem-solving capabilities. Armed with these tools, you are well-equipped to tackle complex calculus problems. Mastery of limits is a key achievement.
Similar Problems (Quick Solutions)
1. Find ##lim_{x \to 2} (3x + 1)##. Answer: 7
2. Evaluate ##lim_{x \to 0} \frac{sin(2x)}{x}##. Answer: 2
3. Determine ##lim_{x \to 1} \frac{x^2 – 1}{x – 1}##. Answer: 2
4. Calculate ##lim_{x \to \infty} \frac{x}{x + 1}##. Answer: 1
5. Solve ##lim_{x \to 0} (1 + x)^{\frac{1}{x}}##. Answer: e
| Function | Limit (x → c) | Notes |
|---|---|---|
| Constant | ##lim_{x \to c} a = a## | a is a constant |
| Identity | ##lim_{x \to c} x = c## | |
| Polynomial | ##lim_{x \to c} p(x) = p(c)## | p(x) is a polynomial |
| Rational | ##lim_{x \to c} \frac{p(x)}{q(x)} = \frac{p(c)}{q(c)}## | q(c) ≠ 0 |
| Exponential | ##lim_{x \to c} e^x = e^c## | |
| Logarithmic | ##lim_{x \to c} ln(x) = ln(c)## | c > 0 |
| Trigonometric (sin) | ##lim_{x \to c} sin(x) = sin(c)## | |
| Trigonometric (cos) | ##lim_{x \to c} cos(x) = cos(c)## | |
| ##\frac{sin(x)}{x}## | ##lim_{x \to 0} \frac{sin(x)}{x} = 1## |
We also Published
RESOURCES
- 2.2 The Limit of a Function – Calculus Volume 1 | OpenStax
- Limit of a function – Wikipedia
- Limits intro (article) | Khan Academy
- Calculus I – The Limit
- How do you calculate the limits of functions using the exponential …
- calculus – Do functions all have an infinite number of limits …
- Limits of Functions | Brilliant Math & Science Wiki
- Manipulation of Functions for Finding Limits : r/math
- Limits of functions
- real analysis – How to calculate limits of functions? – Mathematics …




0 Comments