General aptitude in geometry often involves solving triangle angle problems using ratios. This foundational skill is crucial for competitive exams and enhances logical reasoning through practical mathematical applications.
Table of Contents
Read More
Mastering geometry aptitude problems is essential for competitive exams and academic success. This classic triangle angle ratio question builds foundational skills in spatial reasoning and algebraic application.
Understanding Triangle Angle Ratios
Triangle angle ratios provide a straightforward method to determine unknown angles using proportional relationships. They are a staple in aptitude tests, testing both mathematical and logical thinking.
Ratio Fundamentals
Ratios express the relative sizes of parts in a whole. In a triangle with angles in ratio 2:3:4, the sum of ratio parts is 2+3+4=9. Each part represents a fraction of the total 180 degrees.
This approach simplifies complex problems by breaking them into manageable steps, enhancing problem-solving efficiency.
Application in Geometry
Applying ratios to triangles involves setting up equations based on angle sums. For instance, if angles are proportional, assign variables like 2x, 3x, and 4x, then solve for x using the angle sum property.
This method is versatile, applicable to various polygon problems beyond triangles, making it a key tool in geometry.
Solving the Specific Problem
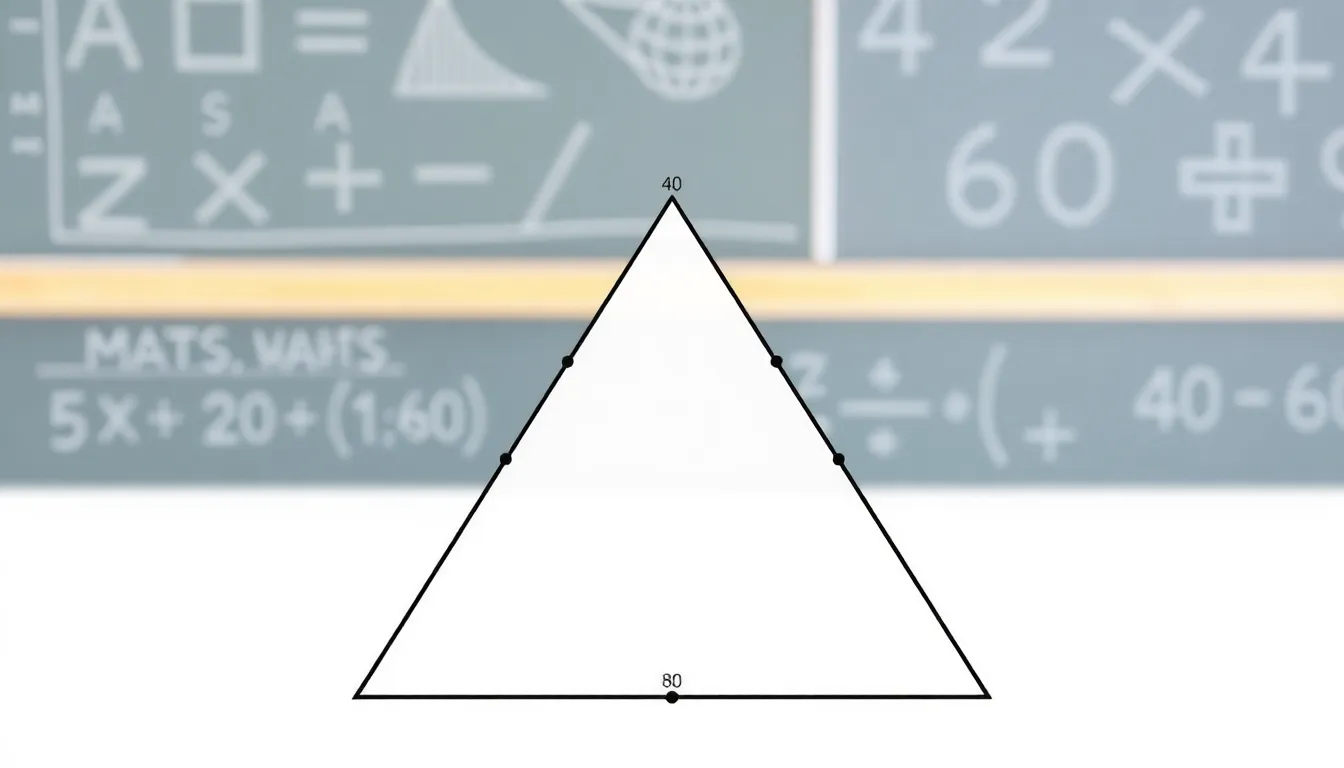
Let’s dive into the given problem: angles in ratio 2:3:4. The largest angle corresponds to the largest ratio part, offering a clear path to the solution.
Step-by-Step Calculation
First, express the angles as 2x, 3x, and 4x. The sum of angles in a triangle is always 180 degrees, so 2x + 3x + 4x = 180. Simplifying, 9x = 180, thus x = 20.
Substitute back: angles are 40, 60, and 80 degrees. The largest angle is 80 degrees, derived from 4 times x.
Verification and Insights
Verify by summing: 40 + 60 + 80 = 180, confirming correctness. This problem illustrates how ratios ensure internal consistency in geometric figures.
Understanding this helps in tackling more advanced problems, such as those involving similar triangles or trigonometric applications.
Key Takeaways
Geometry aptitude problems like this reinforce core concepts. Practice with varied ratios sharpens skills, preparing you for exams and real-world applications in fields like engineering and architecture.
| Ratio Part | Angle Value (Degrees) |
|---|---|
| 2 | 40 |
| 3 | 60 |
| 4 | 80 (Largest) |
We also Published
RESOURCES
- General Aptitude Test – Aptitude-test.com
- General Aptitude Contract : r/AirForceRecruits
- The role of mind-wandering in measurements of general aptitude
- General Aptitude : r/AirForceRecruits
- Fairness in Employment Testing: Validity Generalization, Minority …
- ED164579 – Manual for the USES General Aptitude Test … – ERIC
- GA General Aptitude
- Aptitude Questions and Answers – GeeksforGeeks
- Does anyone have General Aptitude in the Air Force?
- ASVAB – U.S. Air Force





0 Comments