IIT JEE electrostatics is a cornerstone of physics, vital for engineering aspirants. This subject delves into the study of electric charges at rest, a fundamental concept in understanding electromagnetism. This area is integral to comprehending the behavior of matter and energy. This post aims to explore the essential concepts and numerical problems.
Table of Contents
Read More
Mastering iit jee electrostatics is crucial for success in the IIT JEE exam. This article delves into numerical problems based on electric fields, potential, and forces, providing a comprehensive guide for students. Let’s unravel the complexities of electrostatics through detailed explanations and illustrative examples.
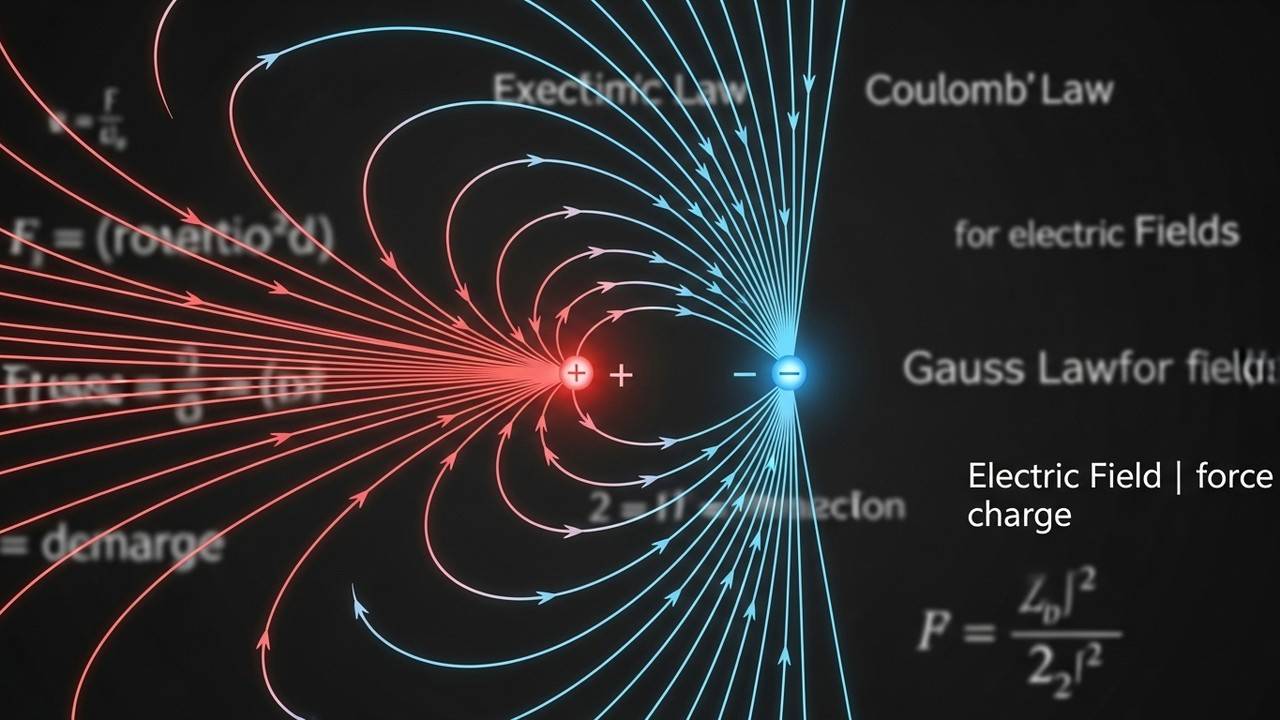
Understanding Coulomb’s Law and Electric Force
The foundation of iit jee electrostatics lies in understanding Coulomb’s Law, which describes the force between two point charges. This law is fundamental and essential for solving a wide range of problems related to electrostatic interactions. Accurate calculations of electric forces are essential for analyzing the behavior of charged particles.
Coulomb’s Law: The Basics
Coulomb’s Law states that the force between two point charges is directly proportional to the product of the charges and inversely proportional to the square of the distance between them. Mathematically, it is represented as:
Where F is the force, q1 and q2 are the charges, r is the distance, and k is Coulomb’s constant (approximately 8.987 × 10^9 N⋅m²/C²). This relationship is the cornerstone of electrostatics, providing the framework for all subsequent calculations. This law underpins the entire field of electrostatics.
We use Coulomb’s Law to calculate the electrostatic force between two charges:
###F = k \dfrac{q_1 q_2}{r^2}###
where: – ##k = 9 \times 10^9 \, N \cdot m^2 / C^2## (Coulomb’s constant) – ##q_1 = 2 \times 10^{-6} \, C## – ##q_2 = 3 \times 10^{-6} \, C## – ##r = 1 \, m##
Substitute the values:
###F = 9 \times 10^9 \cdot \dfrac{(2 \times 10^{-6})(3 \times 10^{-6})}{(1)^2}###
Simplify:
###F = 9 \times 10^9 \cdot 6 \times 10^{-12}###
###F = 54 \times 10^{-3} = 0.054 \, N###
Thus, the electrostatic force between the two charges is 0.054 N. Since both charges are positive, the force is repulsive.
Electric Field and Force
The electric field is a vector field that describes the force exerted on a positive test charge at any given point. It is a crucial concept in electrostatics, providing a way to visualize and quantify the effect of charged particles. Electric fields are essential for understanding the behavior of charges in space.
The electric field (E) due to a point charge (q) at a distance (r) is given by:
The force experienced by a charge in an electric field is given by:
###F = q’ \cdot E###
where: – ##F## = force on the charge (in Newtons) – ##q’## = test charge placed in the field (in Coulombs) – ##E## = electric field intensity (in N/C)
This relation is fundamental in electrostatics, showing how an electric field exerts a force directly proportional to the magnitude of the charge. It is widely applied in analyzing particle motion, capacitor behavior, and field interactions in IIT JEE-level physics problems.
Calculating Electric Potential and Energy
Electric potential and energy are vital concepts in iit jee electrostatics, representing the potential energy per unit charge and the energy stored in an electric field, respectively. Understanding these concepts is essential for analyzing the energy associated with charge distributions. This knowledge is critical for solving problems involving the movement of charges in electric fields.
Electric Potential
Electric potential (V) at a point due to a point charge (q) at a distance (r) is given by:
The electric potential is a scalar quantity, and it is measured in volts. It represents the work done per unit charge to bring a positive test charge from infinity to that point. Electric potential is a foundational concept for understanding the behavior of charges in an electric field.
For example, consider a charge of 5 μC at a distance of 2 meters. The electric potential is calculated as:
This calculation provides insight into the potential energy a charge would have at that location.
Electric Potential Energy
Electric potential energy (U) is the energy stored in a system of charges. For two point charges, q1 and q2, separated by a distance r, the potential energy is:
This energy represents the work done to bring the charges from infinity to their current positions. Electric potential energy is a measure of the interaction between charges and is a key concept in iit jee electrostatics. The total potential energy in a system is the sum of the interactions between all pairs of charges.
If we have two charges, q1 = 2 μC and q2 = 3 μC, at a distance of 1 meter, the potential energy is:
This example illustrates how to calculate the energy stored in a system of charges.
Mastering Electrostatic Problems
To excel in iit jee electrostatics, practice is key. The following are similar problems to test your understanding.
Similar Problems
- Calculate the force between two charges of 4 μC and -6 μC separated by 2 meters. Solution: F ≈ -0.054 N.
- Find the electric field at a point 3 meters from a 10 μC charge. Solution: E ≈ 10000 N/C.
- Determine the potential at a point 4 meters from a -8 μC charge. Solution: V ≈ -18000 V.
- Calculate the potential energy of a system with two charges: 3 μC and -5 μC, separated by 1.5 meters. Solution: U ≈ -0.09 J.
- Find the force between two charges of 1 μC and 2 μC separated by 0.5 meters. Solution: F ≈ 0.072 N.
Key Takeaways
Mastering electrostatics requires a strong grasp of fundamental principles and consistent practice. This guide has equipped you with the necessary tools to solve complex problems. Continuous learning and problem-solving are essential for success in IIT JEE. Remember, the key to excelling in electrostatics is to understand the concepts and apply them to various problems.
| Concept | Formula | Description |
|---|---|---|
| Coulomb’s Law | ##F = k * \frac{{q_1 * q_2}}{{r^2}}## | Describes the force between two point charges. |
| Electric Field | ##E = k * \frac{q}{r^2}## | Represents the force exerted on a positive test charge. |
| Electric Potential | ##V = k * \frac{q}{r}## | The potential energy per unit charge. |
| Electric Potential Energy | ##U = k * \frac{{q_1 * q_2}}{r}## | The energy stored in a system of charges. |
We also Published
RESOURCES
- I am struggling with electrostatics in the JEE physics. Can anyone …
- Can I start current electricity without studying electrostatics? – IIT JEE …
- Electrostatics | Physics | JEE Main Previous Year Questions …
- Electrostatics | IIT JEE Wiki | Fandom
- Electrostatics | Physics | JEE Advanced Previous Year Questions …
- Untitled
- Revision Notes on Electrostatic | askIITians
- Electrostatics JEE Main Previous Year Questions With Solutions
- Electric Field – Study Material for IIT JEE | askIITians
- Physics for IIT – JEE & All Other Engineering Examinations …






0 Comments