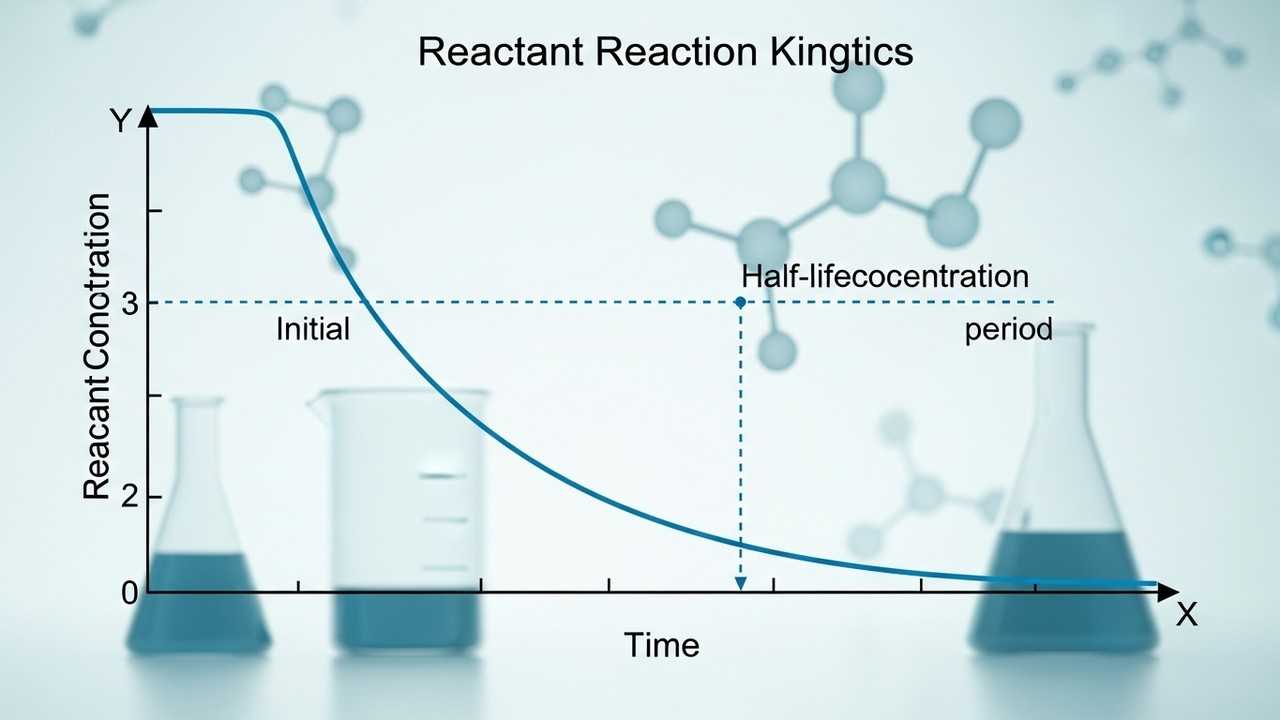
The concept of half-life of a first-order reaction is central to understanding how quickly chemical reactions occur. It allows us to predict the amount of reactant remaining over time. This is a fundamental concept in chemistry and related fields. Understanding half-life is essential for studying reaction rates and chemical kinetics.
Table of Contents
- Understanding First-Order Reactions
- Calculating Reactant Remaining
- Similar Problems and Quick Solutions
- Problem 1: If the half-life is 5 minutes, what fraction remains after 15 minutes?
- Problem 2: Calculate the remaining fraction after 20 minutes with a half-life of 10 minutes.
- Problem 3: A reaction has a half-life of 20 minutes. What is the remaining fraction after 60 minutes?
- Problem 4: If the half-life is 8 minutes, calculate the fraction remaining after 24 minutes.
- Problem 5: A reactant has a half-life of 4 minutes. Determine the fraction left after 12 minutes.
Read More
Let’s delve into the concept of half-life of first-order reaction, a fundamental aspect of chemical kinetics. This topic is crucial for understanding reaction rates and the behavior of chemical reactions over time. We’ll explore how to calculate the remaining reactant after a specific time, using the half-life as our key parameter. This understanding is essential for various applications in chemistry and related fields.
Understanding First-Order Reactions
A first-order reaction is a chemical reaction where the rate of the reaction depends linearly on the concentration of only one reactant. This means the rate is directly proportional to the concentration of that reactant. The half-life of first-order reaction is the time it takes for half of the reactant to be consumed.
The rate law for a first-order reaction is expressed as Rate = k[A], where k is the rate constant and [A] is the concentration of the reactant A. This rate law dictates the speed at which the reaction progresses. The study of first-order reactions is vital for understanding the fundamentals of chemical kinetics.
Calculating Reactant Remaining
Half-Life Concept
The half-life (t₁/₂) is a constant for a given first-order reaction and is independent of the initial concentration. This constancy simplifies calculations involving the half-life of first-order reaction . The half-life allows us to predict the amount of reactant remaining after a certain number of half-lives.
After one half-life, 50% of the reactant remains. After two half-lives, 25% remains, and so on. This predictable decay pattern is a hallmark of first-order kinetics. The formula that connects half-life and rate constant is ##t_{1/2} = 0.693/k##.
Applying to the Problem
Given that the half-life (t₁/₂) is 10 minutes, and the total time is 30 minutes, we can determine how many half-lives have passed. Since 30 minutes is equal to three half-lives (30 minutes / 10 minutes per half-life = 3 half-lives), the calculation is straightforward.
After one half-life, the fraction remaining is 1/2. After two half-lives, it’s (1/2) (1/2) = 1/4. After three half-lives, it’s (1/2) (1/2) * (1/2) = 1/8. This stepwise reduction is a core feature of the half-life of first-order reaction .
Final Solution
Therefore, after 30 minutes, 1/8 of the reactant remains. This means that only one-eighth of the initial amount of the reactant is still present after the three half-lives. This understanding is crucial for chemical reaction analysis.
Similar Problems and Quick Solutions
Problem 1: If the half-life is 5 minutes, what fraction remains after 15 minutes?
Solution: 1/8
Problem 2: Calculate the remaining fraction after 20 minutes with a half-life of 10 minutes.
Solution: 1/4
Problem 3: A reaction has a half-life of 20 minutes. What is the remaining fraction after 60 minutes?
Solution: 1/8
Problem 4: If the half-life is 8 minutes, calculate the fraction remaining after 24 minutes.
Solution: 1/8
Problem 5: A reactant has a half-life of 4 minutes. Determine the fraction left after 12 minutes.
Solution: 1/8
| Time (minutes) | Number of Half-Lives | Fraction of Reactant Remaining |
|---|---|---|
| 0 | 0 | 1 (100%) |
| 10 | 1 | 1/2 (50%) |
| 20 | 2 | 1/4 (25%) |
| 30 | 3 | 1/8 (12.5%) |
We also Published
RESOURCES
- 4.5: First Order Reaction Half-Life – Chemistry LibreTexts
- Half Lives
- 2.3: First-Order Reactions – Chemistry LibreTexts
- Half-Life of a Chemical Reaction
- Why is the half-life constant for a first-order reaction? | TutorChase
- Half life formula for Zero order reaction
- How to Calculate Half-life of a First order Reaction | Chemistry …
- Half-life and reaction order | Physical Chemistry I Class Notes …
- Half-Life (first order)
- Kinetics: first-order chemical reactions – ChemTeam



0 Comments