Symmetry in Coordinate Geometry is fundamental for understanding geometric shapes and their properties within the Cartesian plane. We’ll explore different types of symmetry, learn how to identify them, and see how they simplify problem-solving in coordinate geometry. Understanding symmetry is crucial for visualizing and analyzing geometric figures, and it has applications in various fields, including art, architecture, and physics. The symmetry in coordinate geometry is an essential concept.

Firstly, we’ll define what symmetry actually means in the context of coordinate geometry. Then, we’ll look at different types of symmetry, such as symmetry about the x-axis, y-axis, and the origin, to give you a solid foundation. Also, we will discuss how to identify these symmetries and how they can be used to simplify problem-solving.

What is Symmetry?

In simple terms, symmetry means that a shape or object remains unchanged after a certain transformation. This transformation could be a reflection, rotation, or translation. In coordinate geometry, we primarily focus on reflectional symmetry (also known as mirror symmetry) and rotational symmetry. Our primary focus will be on reflectional symmetry, where a shape is reflected across a line (the line of symmetry) and remains unchanged.

Types of Symmetry in Coordinate Geometry

There are several types of symmetry we’ll explore, each defined by the line or point about which the symmetry occurs. Understanding these types will allow you to analyze and solve a wide range of geometric problems. The different types of symmetry in coordinate geometry are as follows:

• Symmetry about the x-axis
• Symmetry about the y-axis
• Symmetry about the origin
• Symmetry about the line y = x
• Symmetry about the line y = -x

1. Symmetry about the x-axis

A point is symmetric about the x-axis if its y-coordinate changes sign, while the x-coordinate remains the same. Imagine the x-axis as a mirror. The reflection of a point across this mirror will have the same x-coordinate but an opposite y-coordinate. The symmetry in coordinate geometry with respect to x-axis is a key concept.

Rule: If a point (x, y) is symmetric about the x-axis, its reflected point is (x, -y).

Example 1:

Consider the point A(2, 3). Its reflection across the x-axis, which we’ll call A’, will have coordinates (2, -3). The x-coordinate remains 2, while the y-coordinate changes from 3 to -3.

Example 2:

If a curve is symmetric about the x-axis, then for every point (x, y) on the curve, the point (x, -y) must also lie on the curve. For example, the equation ##y^2 = x## represents a parabola that is symmetric about the x-axis. If we substitute (x, -y) into the equation, we get ##(-y)^2 = x##, which simplifies to ##y^2 = x##, the same as the original equation. This confirms the symmetry.

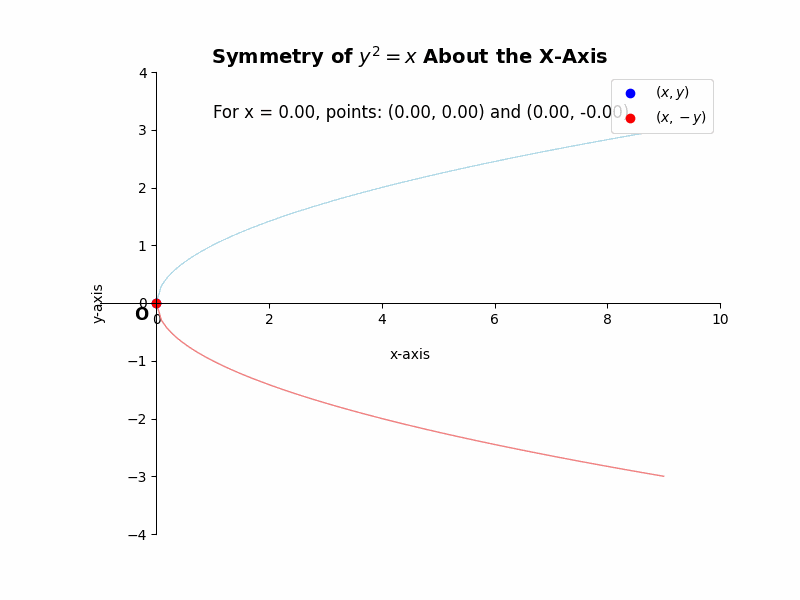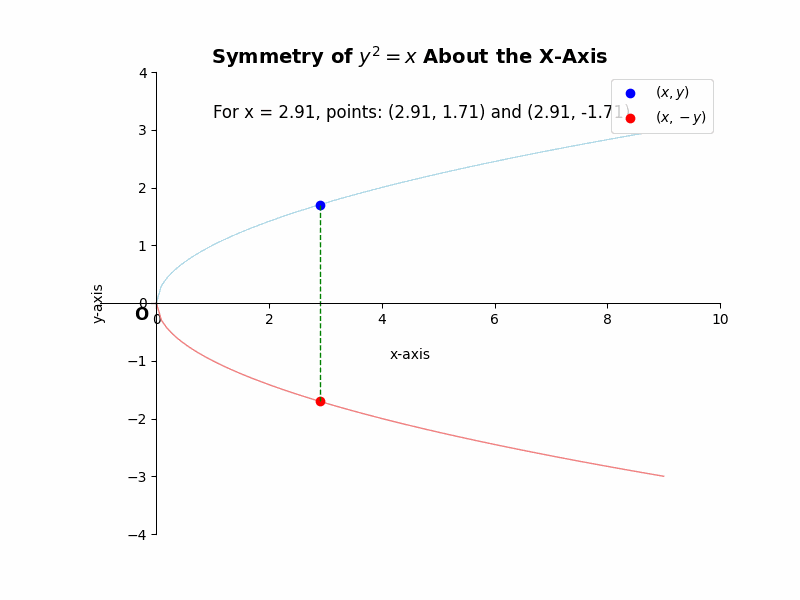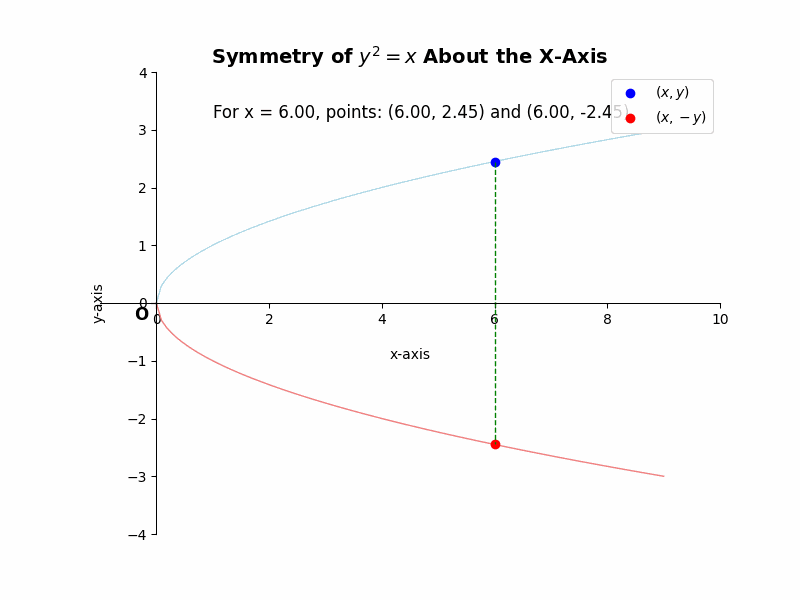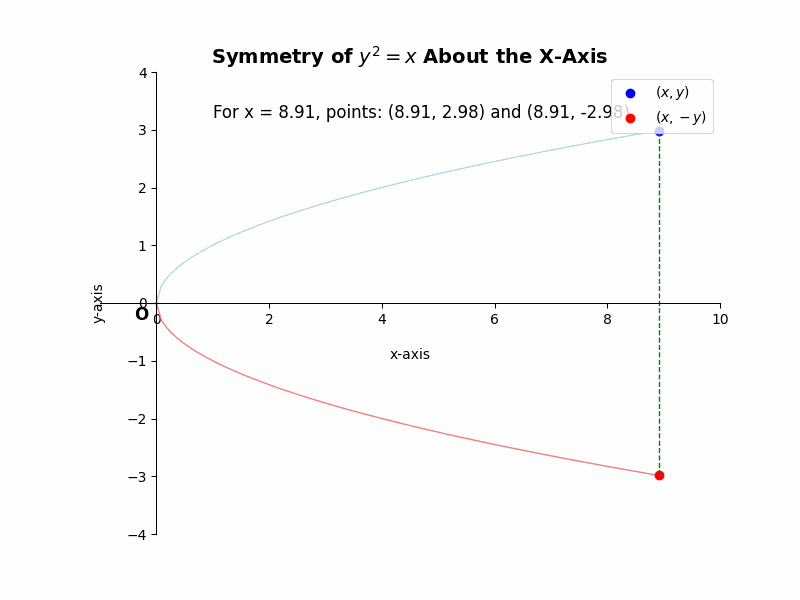
Illustrative Example:

Consider the graph of the equation ##y = x^3 – x##. To check for symmetry about the origin, we replace x with -x and y with -y:

### -y = (-x)^3 – (-x) ### ### -y = -x^3 + x ### ### y = x^3 – x ###

Since the original equation and the transformed equation are not the same, the graph is not symmetric about the x-axis.

2. Symmetry about the y-axis

A point is symmetric about the y-axis if its x-coordinate changes sign, while the y-coordinate remains the same. In this case, the y-axis acts as the mirror. The reflection of a point across the y-axis will have the same y-coordinate but an opposite x-coordinate. This is another fundamental aspect of symmetry in coordinate geometry.

Rule: If a point (x, y) is symmetric about the y-axis, its reflected point is (-x, y).

Example 1:

Consider the point B(4, 1). Its reflection across the y-axis, B’, will have coordinates (-4, 1). The y-coordinate remains 1, while the x-coordinate changes from 4 to -4.

Example 2:

If a curve is symmetric about the y-axis, then for every point (x, y) on the curve, the point (-x, y) must also lie on the curve. For example, the equation ##x^2 + y^2 = 9## represents a circle centered at the origin with a radius of 3. If we substitute (-x, y) into the equation, we get ##(-x)^2 + y^2 = 9##, which simplifies to ##x^2 + y^2 = 9##, the same as the original equation. This confirms the symmetry.

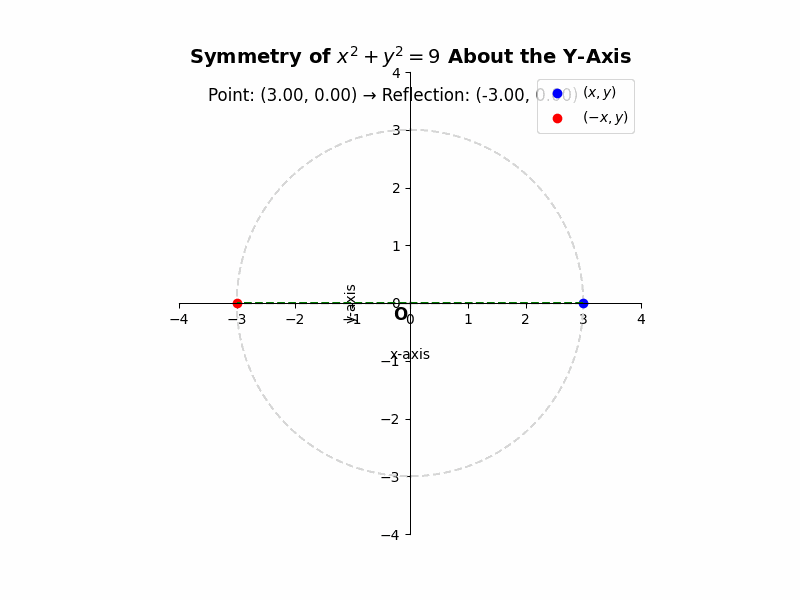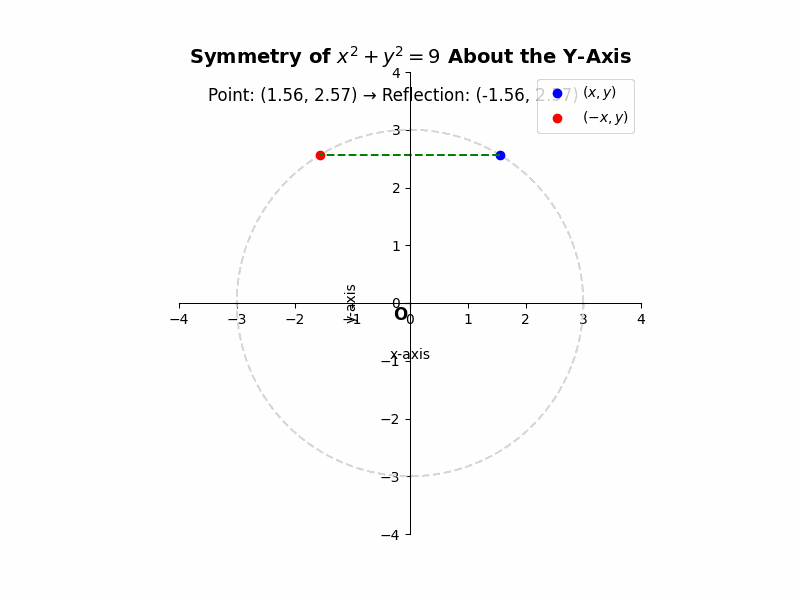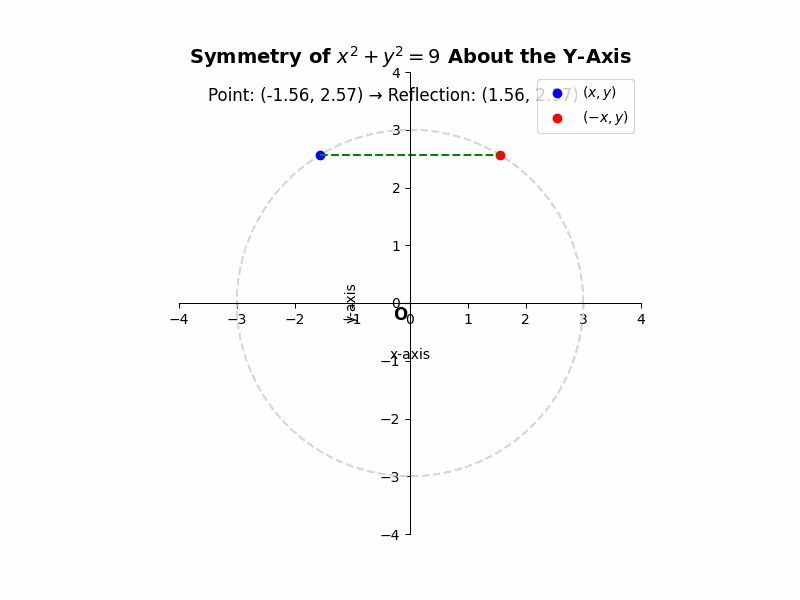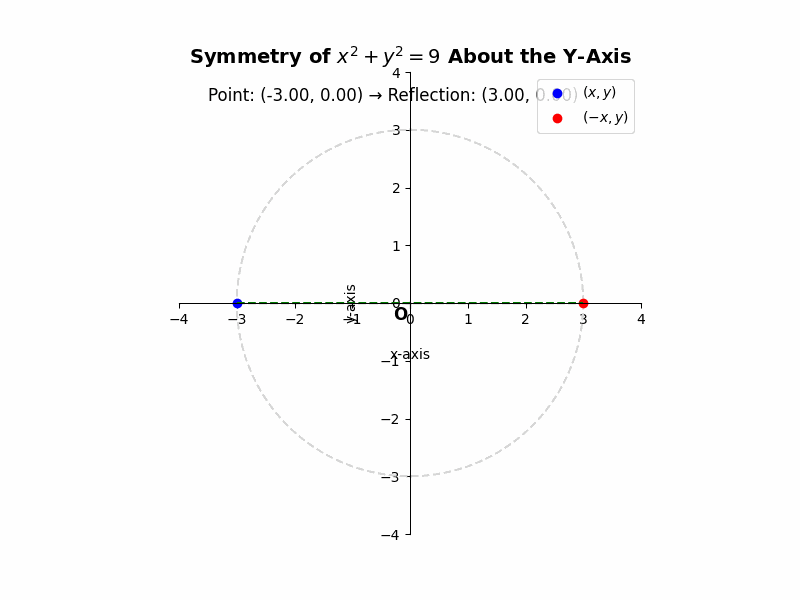
Illustrative Example:

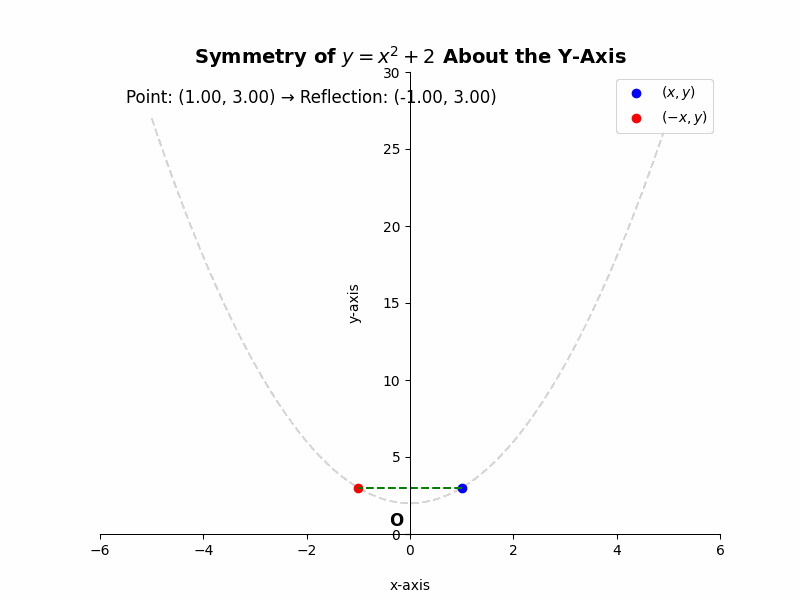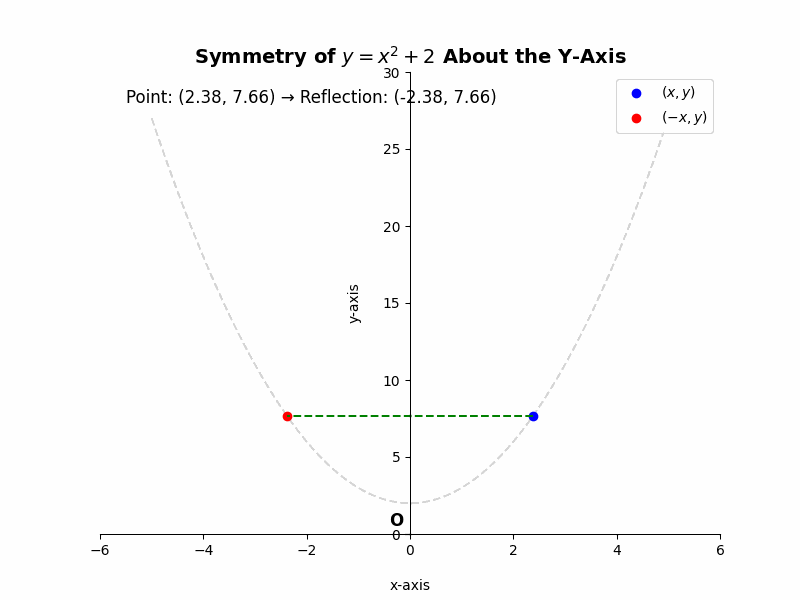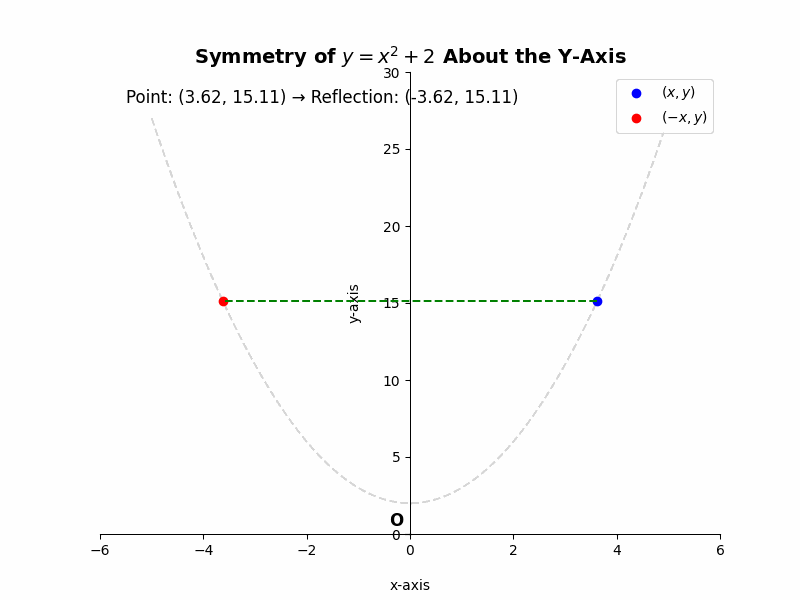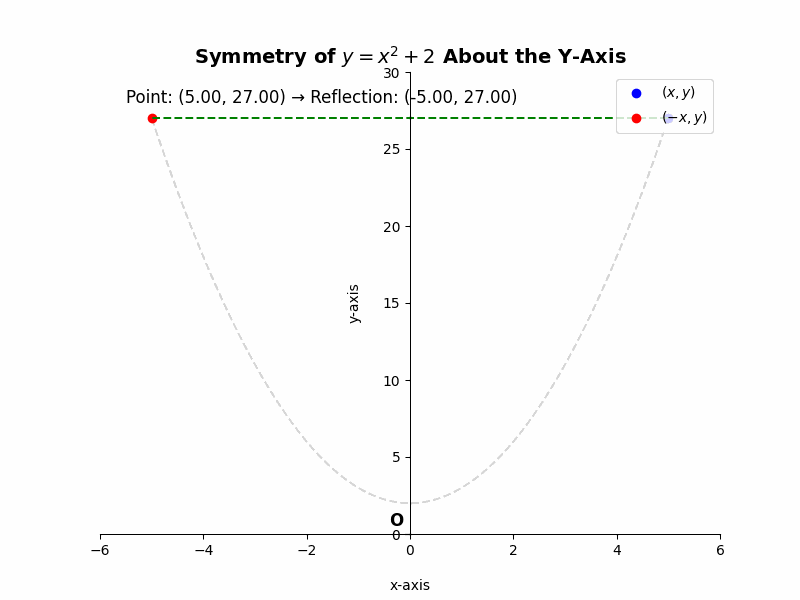
Consider the graph of the equation ##y = x^2 + 2##. To check for symmetry about the y-axis, we replace x with -x:

### y = (-x)^2 + 2 ### ### y = x^2 + 2 ###

Since the original equation and the transformed equation are the same, the graph is symmetric about the y-axis.

3. Symmetry about the Origin

A point is symmetric about the origin if both its x-coordinate and y-coordinate change signs. This is equivalent to a 180-degree rotation around the origin. The origin acts as the center of symmetry. Understanding symmetry about the origin is an important part of symmetry in coordinate geometry.

Rule: If a point (x, y) is symmetric about the origin, its reflected point is (-x, -y).

Example 1:

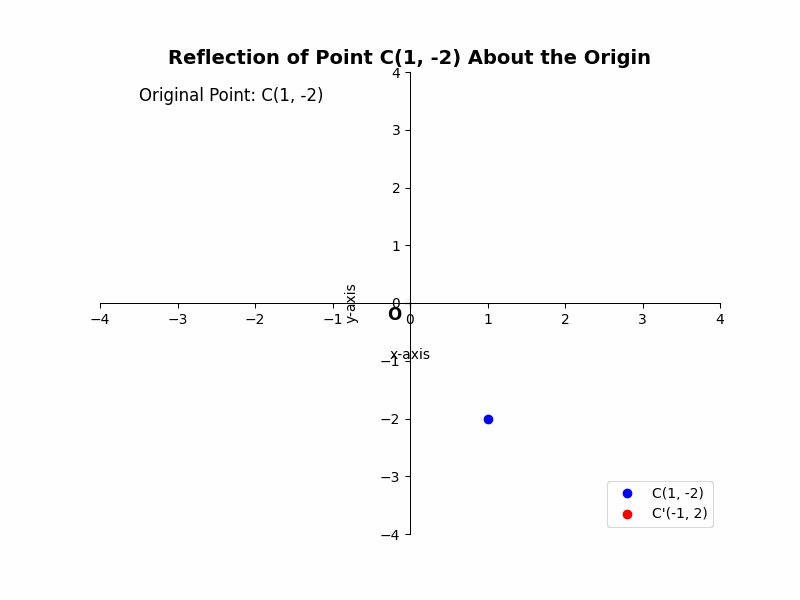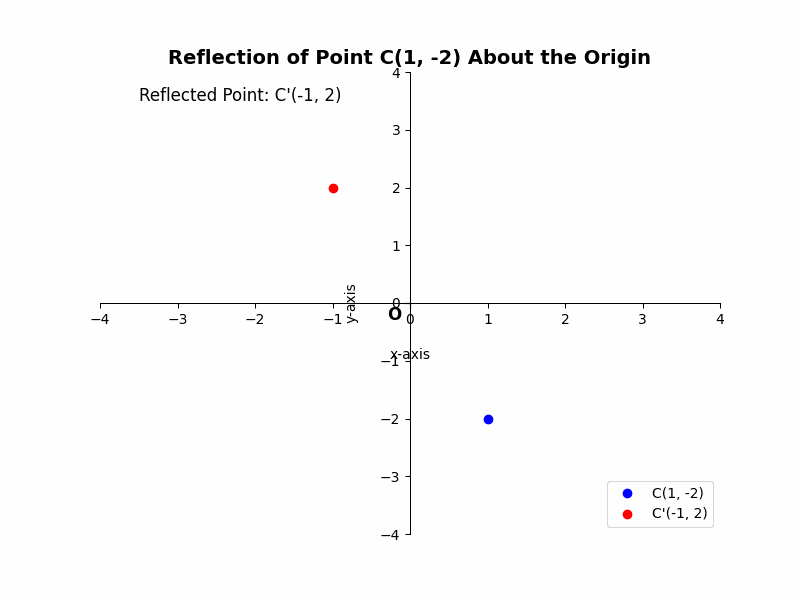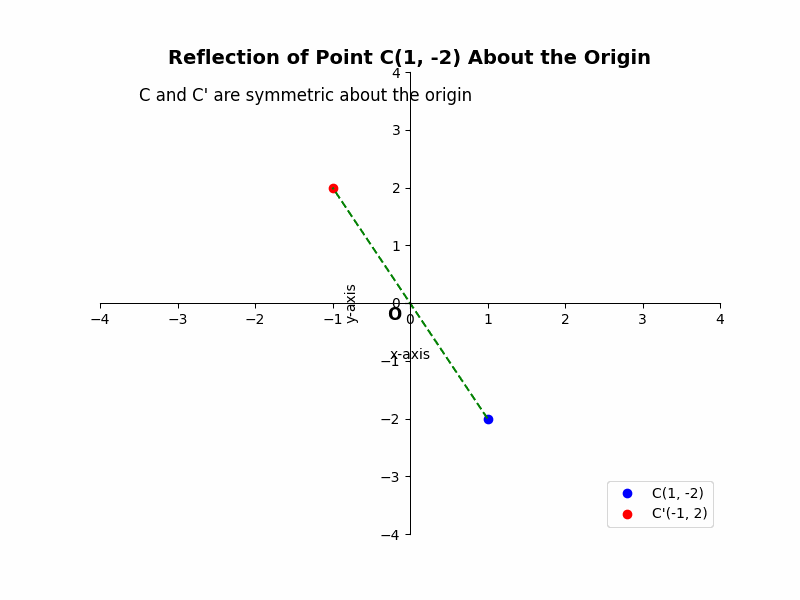
Consider the point C(1, -2). Its reflection about the origin, C’, will have coordinates (-1, 2). Both the x and y coordinates have changed signs.

Example 2:

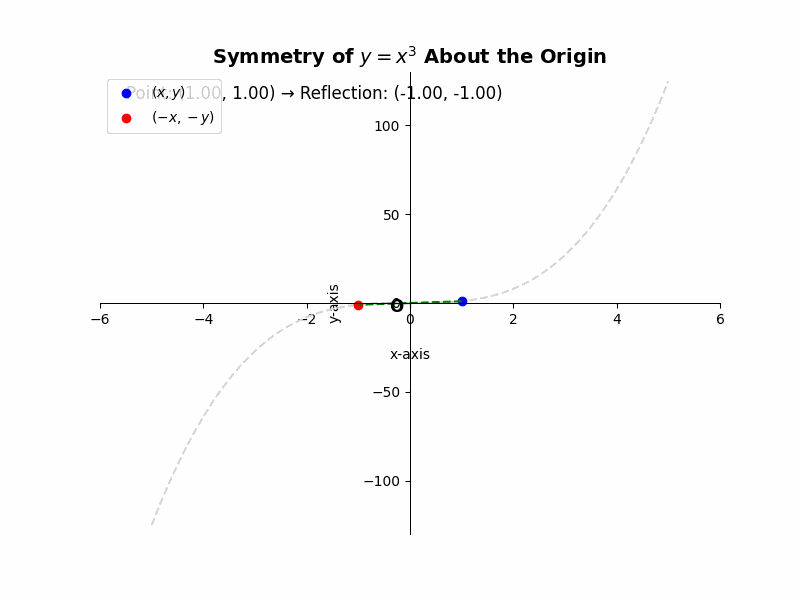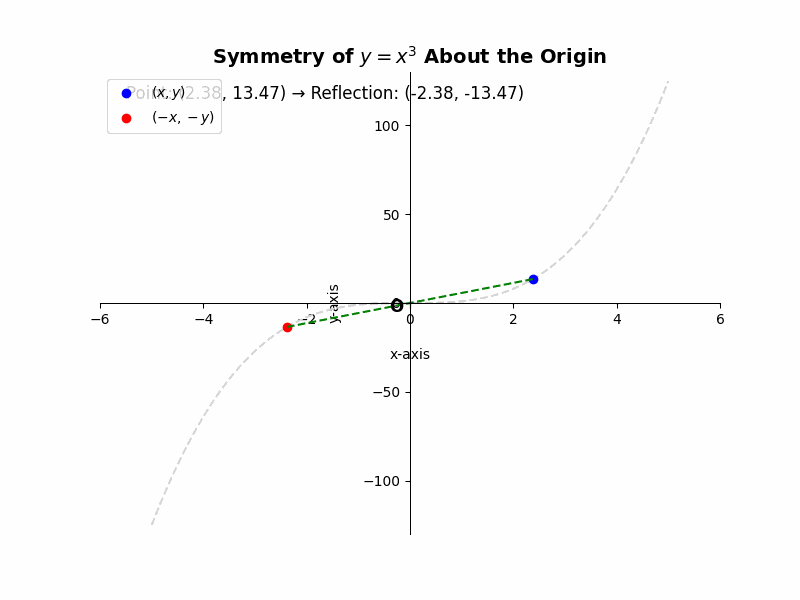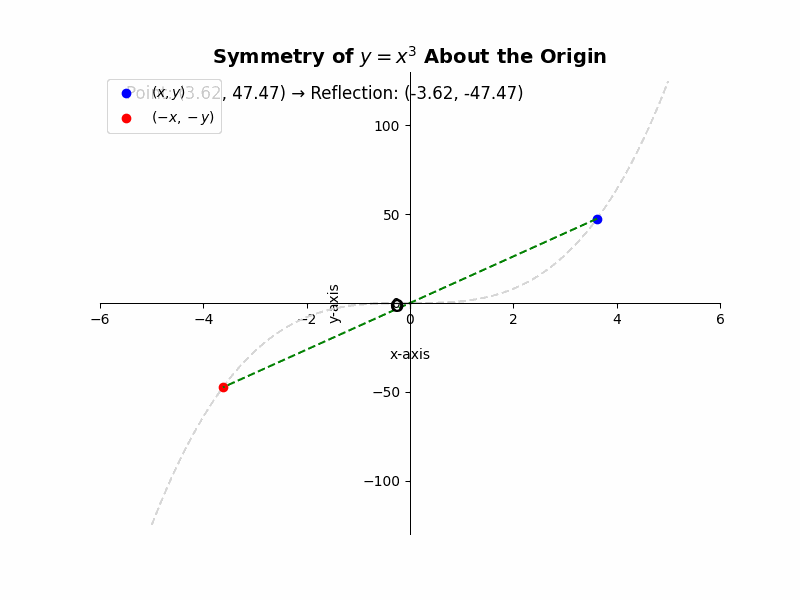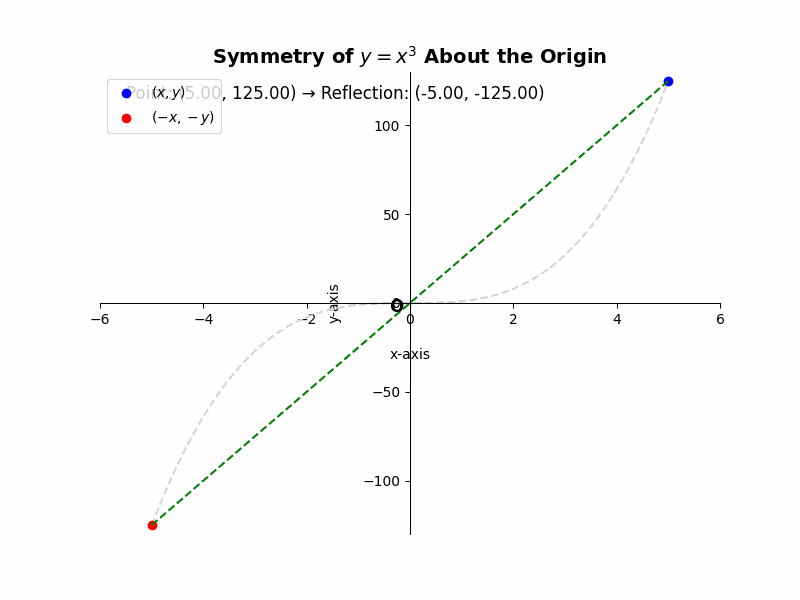
If a curve is symmetric about the origin, then for every point (x, y) on the curve, the point (-x, -y) must also lie on the curve. For example, the equation ##y = x^3## represents a cubic function that is symmetric about the origin. If we substitute (-x, -y) into the equation, we get ##-y = (-x)^3##, which simplifies to ##-y = -x^3##, or ##y = x^3##, the same as the original equation. This confirms the symmetry.

Illustrative Example:

Consider the graph of the equation ##y = x^3 – x##. To check for symmetry about the origin, we replace x with -x and y with -y:

### -y = (-x)^3 – (-x) ###

### -y = -x^3 + x ###

### y = x^3 – x ###

Since the original equation and the transformed equation are the same, the graph is symmetric about the origin.

4. Symmetry about the Line y = x

A point is symmetric about the line y = x if its x and y coordinates are interchanged. Imagine folding the coordinate plane along the line y = x; the two halves of the shape will perfectly overlap. This type of symmetry is less common but equally important in the context of symmetry in coordinate geometry.

Rule: If a point (x, y) is symmetric about the line y = x, its reflected point is (y, x).

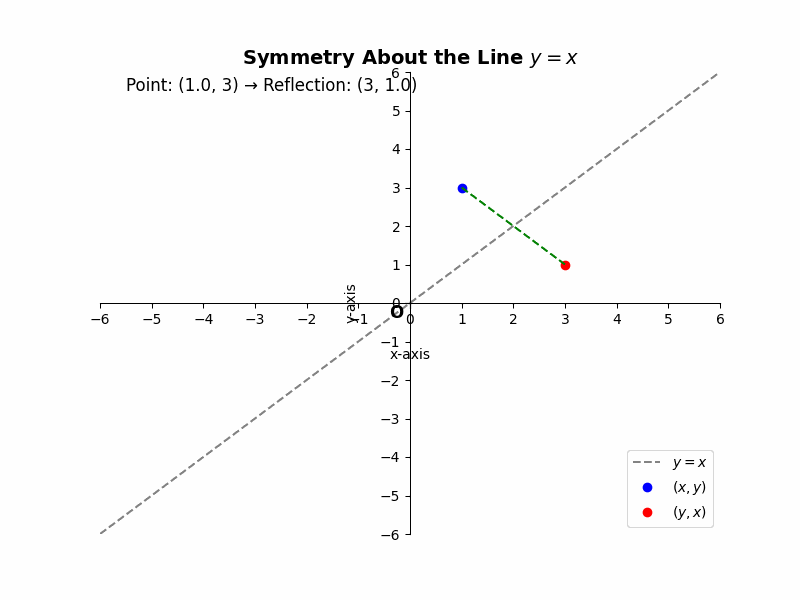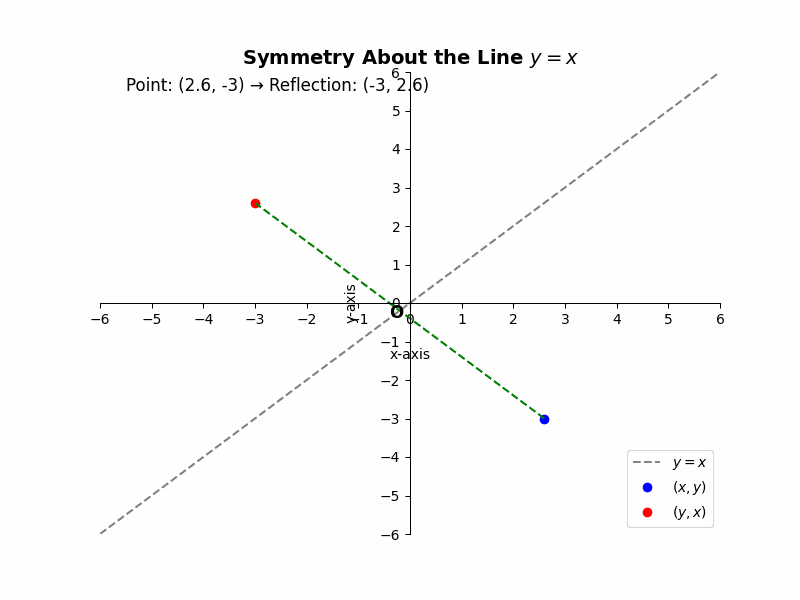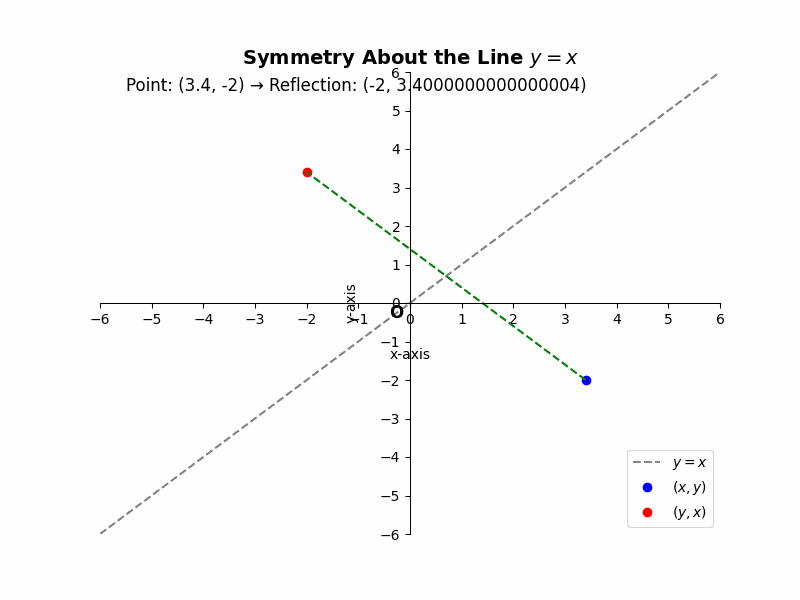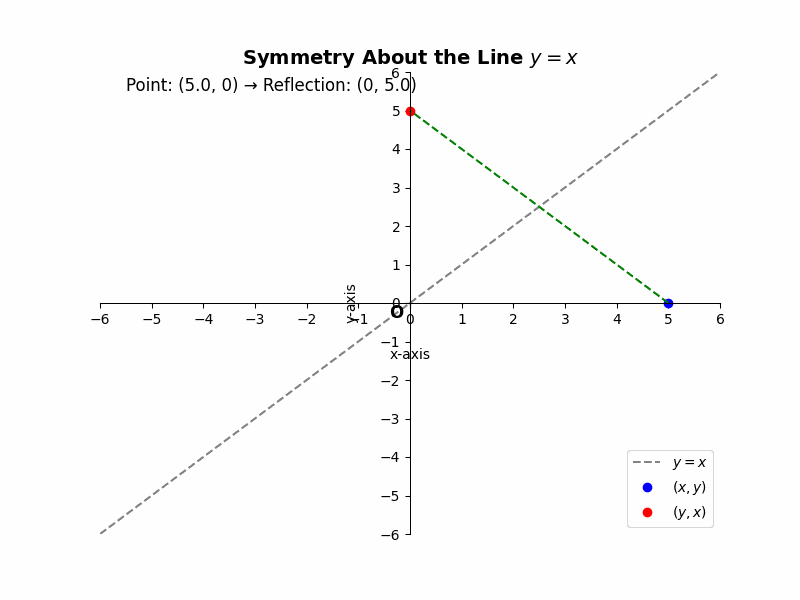
Example 1:

Consider the point D(5, 7). Its reflection across the line y = x, D’, will have coordinates (7, 5). The x and y coordinates have swapped positions.

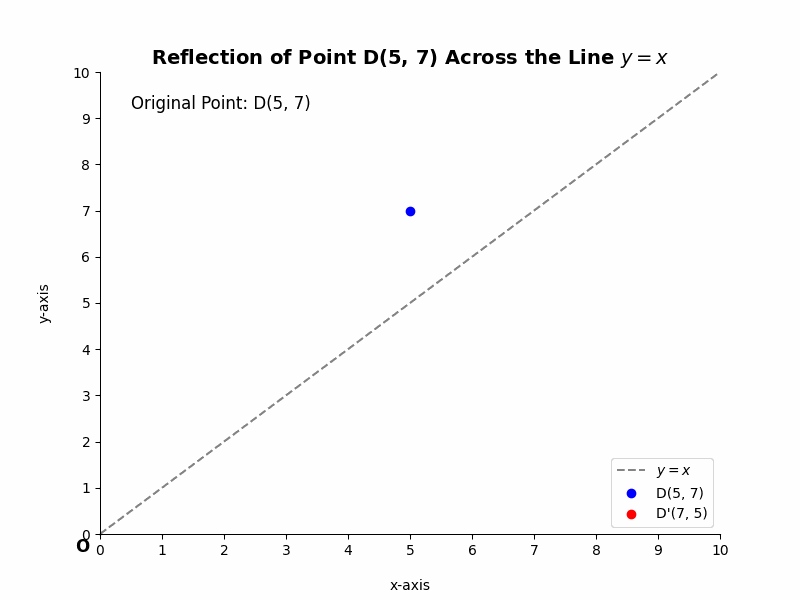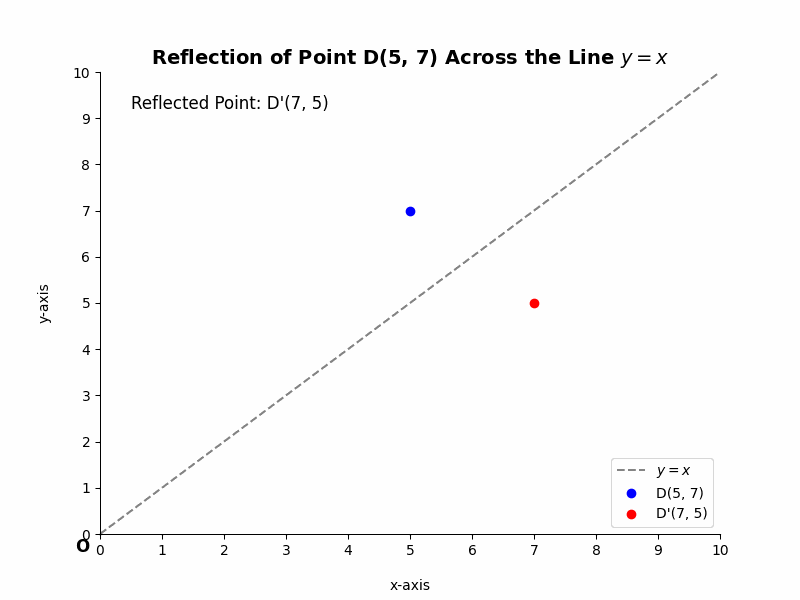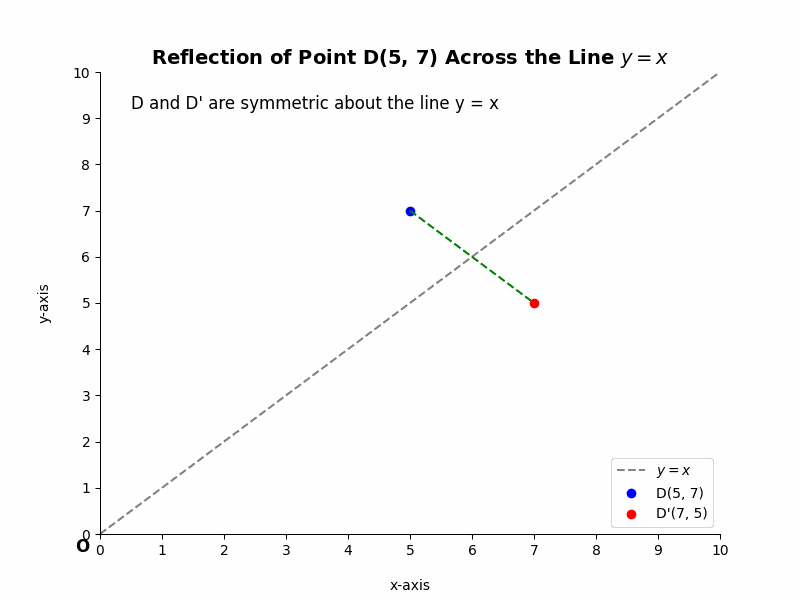
Example 2:

If a curve is symmetric about the line y = x, then for every point (x, y) on the curve, the point (y, x) must also lie on the curve. For example, the equation ##y = \\\\frac{1}{x}## represents a hyperbola that is symmetric about the line y = x. If we substitute (y, x) into the equation, we get ##x = \\\\frac{1}{y}##, which is equivalent to ##y = \\\\frac{1}{x}##, the same as the original equation. This confirms the symmetry.

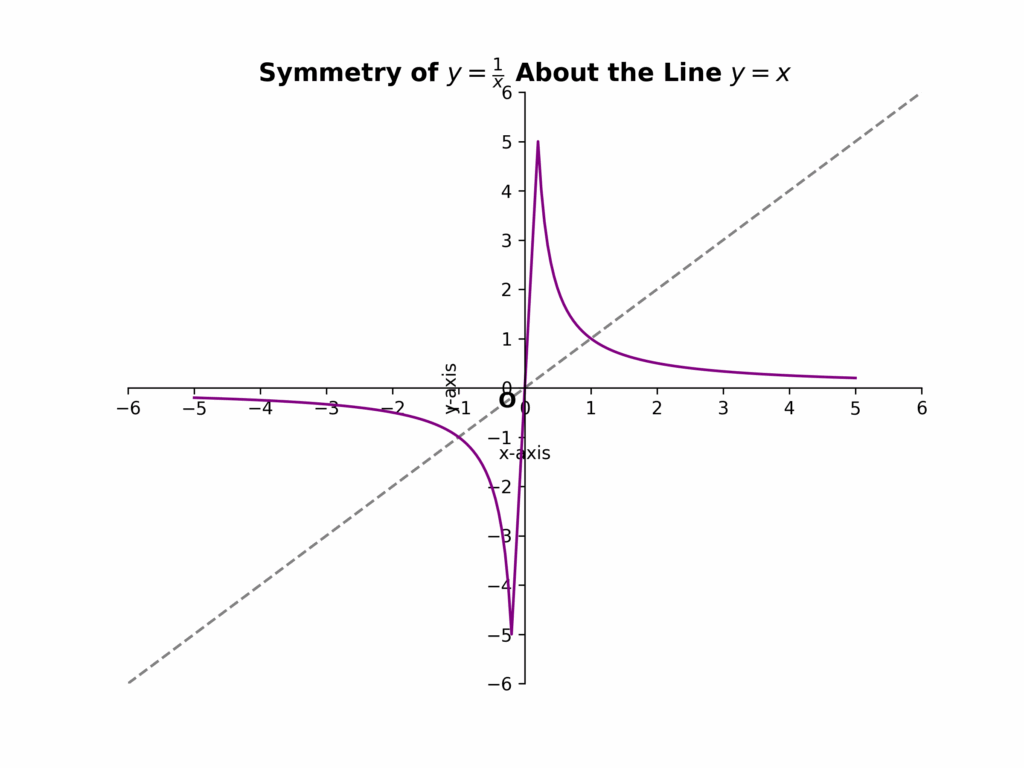
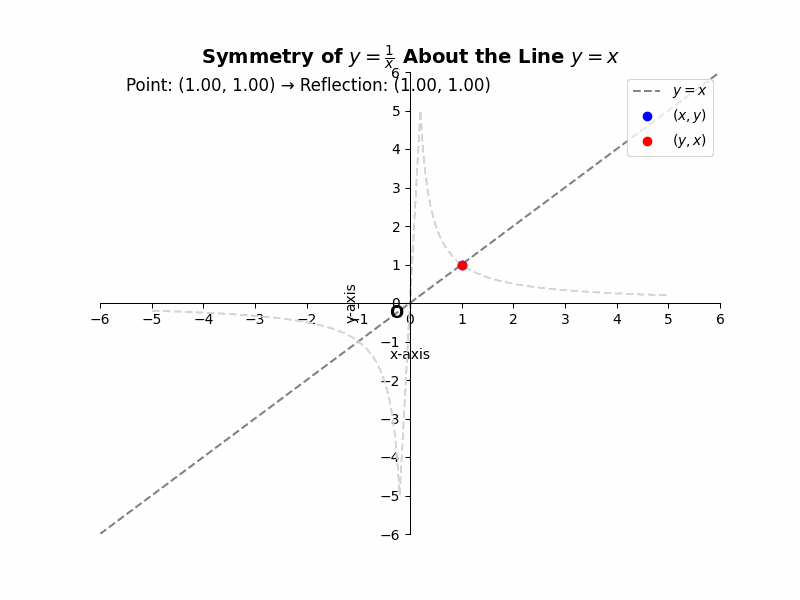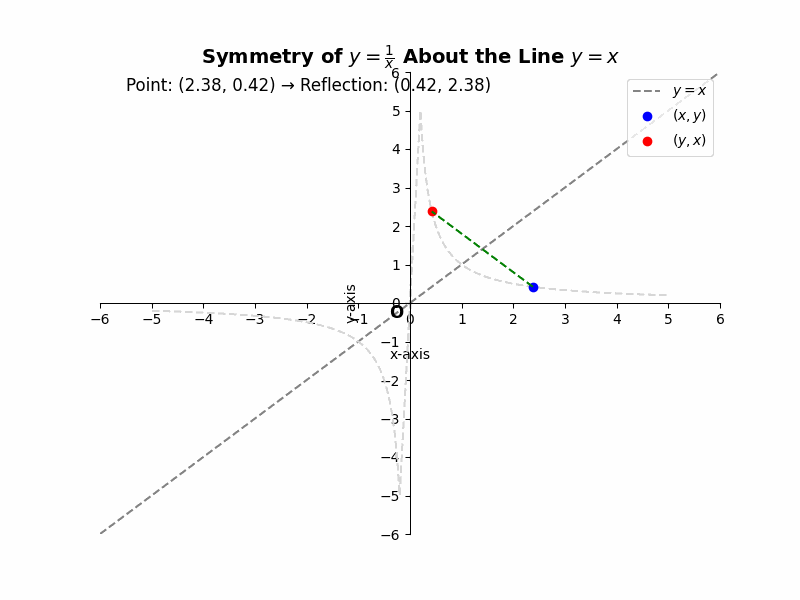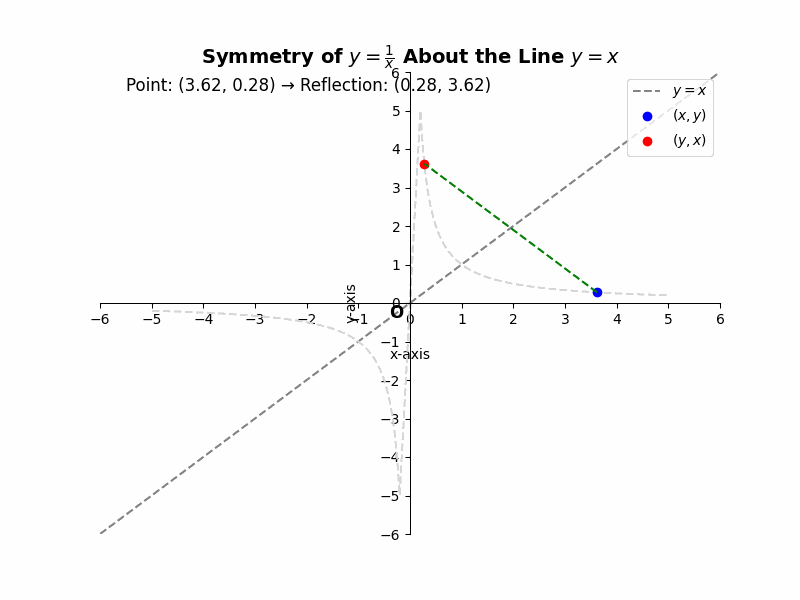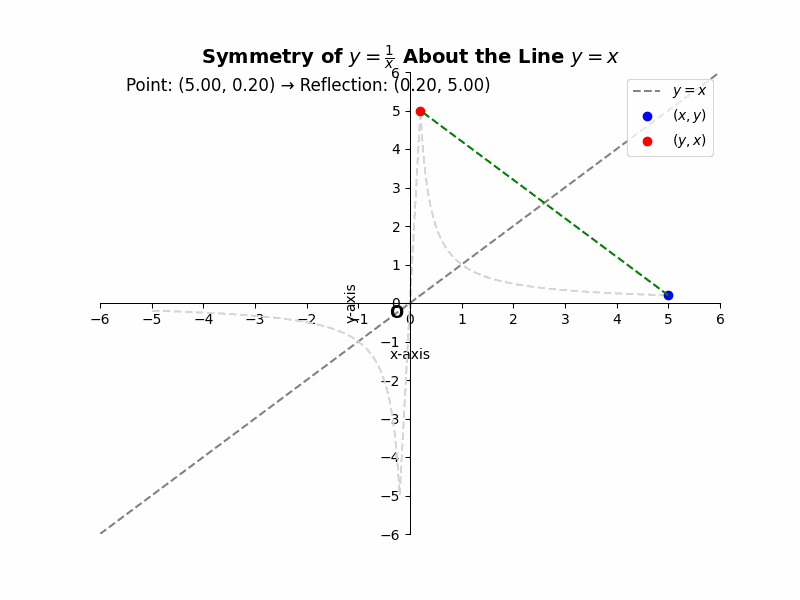
Illustrative Example:

Consider the graph of the equation ##y = 2x + 3##. To check for symmetry about the line y = x, we swap x and y:

### x = 2y + 3 ###

### y = \\frac{x – 3}{2} ###

Since the original equation and the transformed equation are not the same, the graph is not symmetric about the line y = x.

5. Symmetry about the Line y = -x

A point is symmetric about the line y = -x if its x and y coordinates are interchanged and their signs are changed. This is similar to symmetry about y = x, but with an additional sign change. This concept is a vital aspect of symmetry in coordinate geometry.

Rule: If a point (x, y) is symmetric about the line y = -x, its reflected point is (-y, -x).

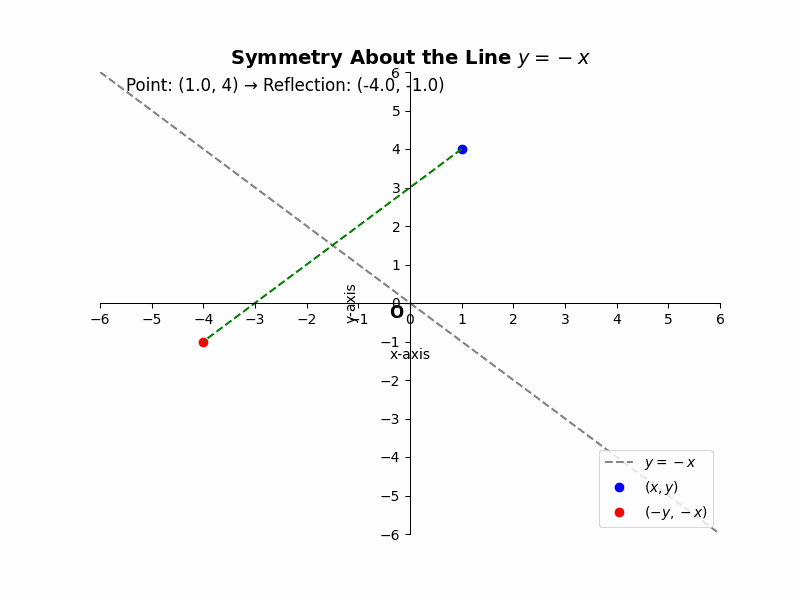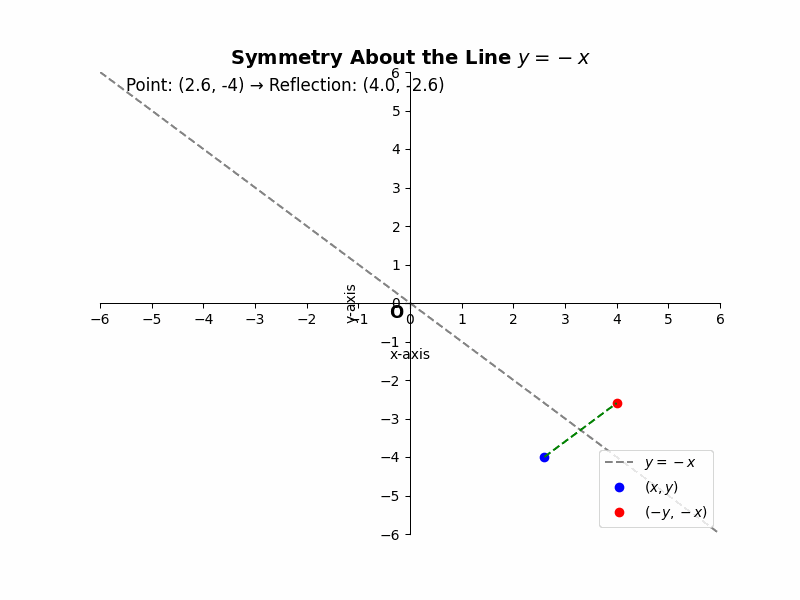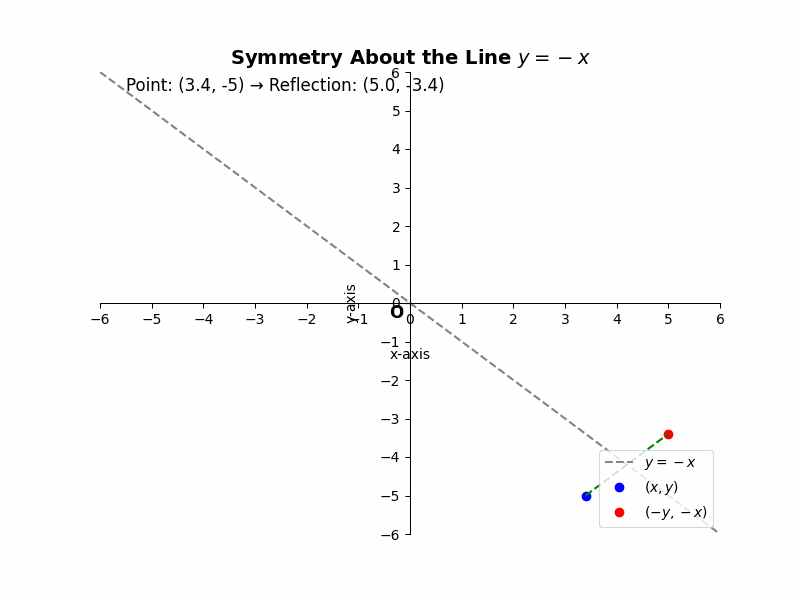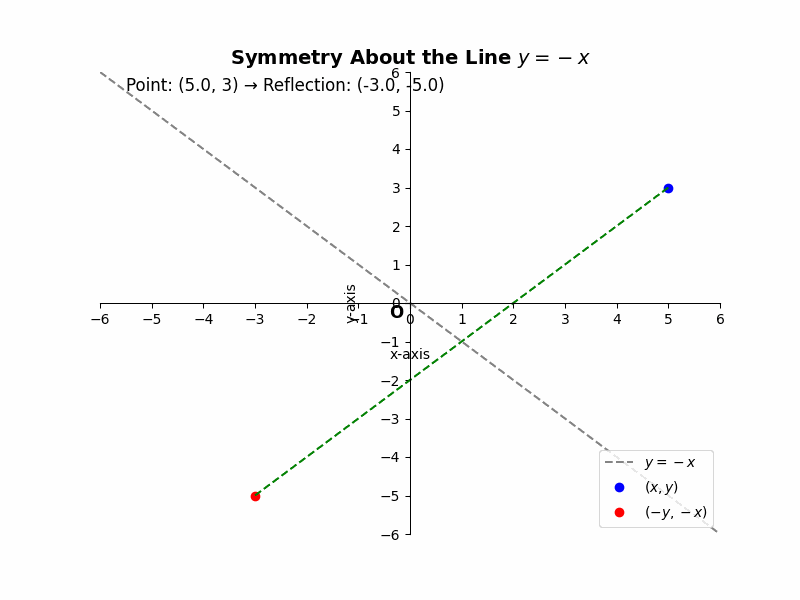
Example 1:

Consider the point E(2, -4). Its reflection across the line y = -x, E’, will have coordinates (4, -2). The x and y coordinates have swapped positions, and their signs have changed.

Example 2:

If a curve is symmetric about the line y = -x, then for every point (x, y) on the curve, the point (-y, -x) must also lie on the curve. For example, the equation ##xy = 4## represents a hyperbola that is symmetric about the line y = -x. If we substitute (-y, -x) into the equation, we get ##(-y)(-x) = 4##, which simplifies to ##xy = 4##, the same as the original equation. This confirms the symmetry.

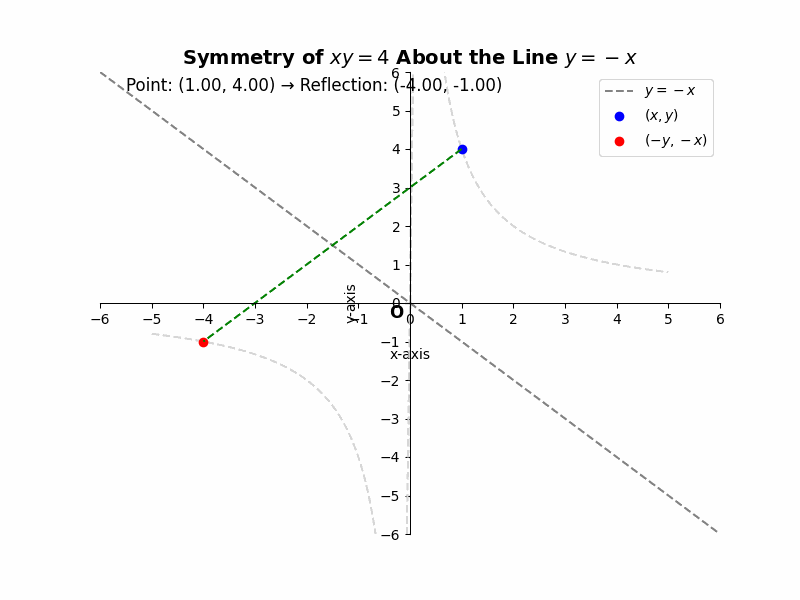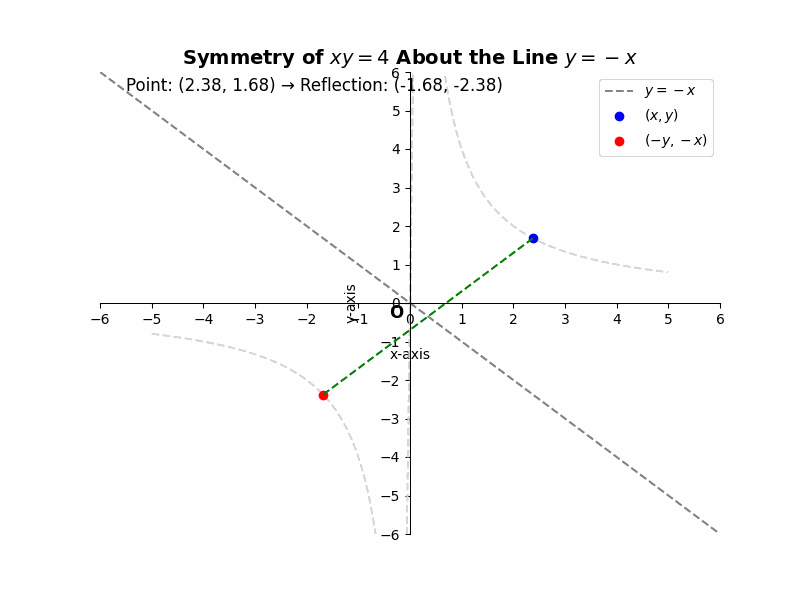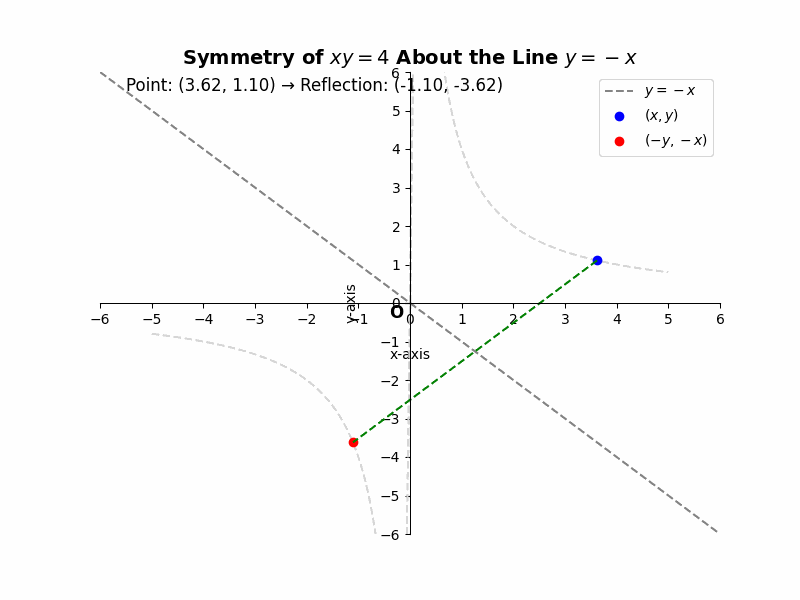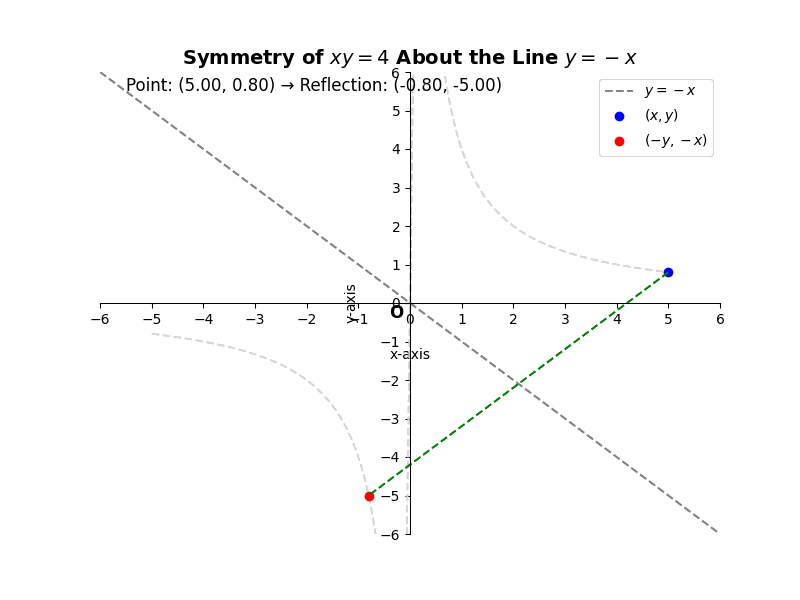
Illustrative Example:

Consider the graph of the equation ##x^2 – y^2 = 1##. To check for symmetry about the line y = -x, we swap x with -y and y with -x:

### (-y)^2 – (-x)^2 = 1 ###

### y^2 – x^2 = 1 ###

### x^2 – y^2 = -1 ###

Since the original equation and the transformed equation are not the same, the graph is not symmetric about the line y = -x.

Identifying Symmetry in Equations

We can determine the type of symmetry a curve possesses by analyzing its equation. Here’s a summary of the rules:

• Symmetry about the x-axis: Replace y with -y. If the equation remains unchanged, it’s symmetric about the x-axis.
• Symmetry about the y-axis: Replace x with -x. If the equation remains unchanged, it’s symmetric about the y-axis.
• Symmetry about the origin: Replace x with -x and y with -y. If the equation remains unchanged, it’s symmetric about the origin.
• Symmetry about the line y = x: Swap x and y. If the equation remains unchanged, it’s symmetric about the line y = x.
• Symmetry about the line y = -x: Replace x with -y and y with -x. If the equation remains unchanged, it’s symmetric about the line y = -x.

Examples and Applications

Let’s look at some examples to solidify your understanding. These examples showcase how symmetry can be used to solve problems and analyze different types of equations. These are important aspects of symmetry in coordinate geometry.

Example 1: Symmetry of a Circle

Consider the equation of a circle centered at the origin: ##x^2 + y^2 = r^2##, where r is the radius.

• Symmetry about the x-axis: Replace y with -y: ##x^2 + (-y)^2 = r^2##, which simplifies to ##x^2 + y^2 = r^2##. The equation remains unchanged, so it’s symmetric about the x-axis.
• Symmetry about the y-axis: Replace x with -x: ##(-x)^2 + y^2 = r^2##, which simplifies to ##x^2 + y^2 = r^2##. The equation remains unchanged, so it’s symmetric about the y-axis.
• Symmetry about the origin: Replace x with -x and y with -y: ##(-x)^2 + (-y)^2 = r^2##, which simplifies to ##x^2 + y^2 = r^2##. The equation remains unchanged, so it’s symmetric about the origin.
• Symmetry about the line y = x: Swap x and y: ##y^2 + x^2 = r^2##, which is the same as ##x^2 + y^2 = r^2##. The equation remains unchanged, so it’s symmetric about the line y = x.
• Symmetry about the line y = -x: Replace x with -y and y with -x: ##(-y)^2 + (-x)^2 = r^2##, which simplifies to ##y^2 + x^2 = r^2##, which is the same as ##x^2 + y^2 = r^2##. The equation remains unchanged, so it’s symmetric about the line y = -x.

Therefore, a circle centered at the origin exhibits all types of symmetry.

Example 2: Symmetry of a Parabola

Consider the equation of a parabola: ##y = x^2##.

• Symmetry about the x-axis: Replace y with -y: ##-y = x^2##, or ##y = -x^2##. The equation changes, so it is not symmetric about the x-axis.
• Symmetry about the y-axis: Replace x with -x: ##y = (-x)^2##, which simplifies to ##y = x^2##. The equation remains unchanged, so it’s symmetric about the y-axis.
• Symmetry about the origin: Replace x with -x and y with -y: ##-y = (-x)^2##, which simplifies to ##-y = x^2##, or ##y = -x^2##. The equation changes, so it is not symmetric about the origin.
• Symmetry about the line y = x: Swap x and y: ##x = y^2##. The equation changes, so it is not symmetric about the line y = x.
• Symmetry about the line y = -x: Replace x with -y and y with -x: ##-x = (-y)^2##, which simplifies to ##-x = y^2##, or ##x = -y^2##. The equation changes, so it is not symmetric about the line y = -x.

Therefore, the parabola ##y = x^2## is only symmetric about the y-axis.

Example 3: Symmetry of a Hyperbola

Consider the equation of a hyperbola: ##\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1##.

• Symmetry about the x-axis: Replace y with -y: ##\frac{x^2}{a^2} – \frac{(-y)^2}{b^2} = 1##, which simplifies to ##\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1##. The equation remains unchanged, so it’s symmetric about the x-axis.
• Symmetry about the y-axis: Replace x with -x: ##\frac{(-x)^2}{a^2} – \frac{y^2}{b^2} = 1##, which simplifies to ##\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1##. The equation remains unchanged, so it’s symmetric about the y-axis.
• Symmetry about the origin: Replace x with -x and y with -y: ##\frac{(-x)^2}{a^2} – \frac{(-y)^2}{b^2} = 1##, which simplifies to ##\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1##. The equation remains unchanged, so it’s symmetric about the origin.
• Symmetry about the line y = x: Swap x and y: ##\frac{y^2}{a^2} – \frac{x^2}{b^2} = 1##. The equation changes, so it is not symmetric about the line y = x.
• Symmetry about the line y = -x: Replace x with -y and y with -x: ##\frac{(-y)^2}{a^2} – \frac{(-x)^2}{b^2} = 1##, which simplifies to ##\frac{y^2}{a^2} – \frac{x^2}{b^2} = 1##. The equation changes, so it is not symmetric about the line y = -x.
• Therefore, the hyperbola ##\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1## is symmetric about the x-axis, the y-axis, and the origin.

Therefore, the hyperbola ##\frac{x^2}{a^2} – \frac{y^2}{b^2} = 1## is symmetric about the x-axis, the y-axis, and the origin.

Applications of Symmetry

Symmetry is not just a theoretical concept; it has practical applications in various fields:

• Art and Design: Symmetry is a fundamental principle in art and design, used to create balance, harmony, and aesthetic appeal. Many artistic compositions and architectural designs utilize symmetry.
• Architecture: Symmetry is a key element in architectural design, providing stability and visual harmony to buildings.
• Physics: Symmetry plays a crucial role in physics, particularly in the study of forces, fields, and particles. Symmetry principles are used to simplify complex problems and understand the fundamental laws of nature.
• Engineering: Symmetry is used in engineering design to optimize structures and systems. Symmetric designs often have better performance characteristics.
• Computer Graphics: Symmetry is used in computer graphics to create realistic and efficient models. By exploiting symmetry, artists can reduce the amount of data needed to represent a 3D object.

Problem-Solving with Symmetry

Understanding symmetry can significantly simplify problem-solving in coordinate geometry. Here’s how:

• Finding Points: If you know a point on a curve and the curve is symmetric about a line or point, you can easily find other points on the curve.
• Simplifying Calculations: Symmetry can help simplify calculations. For example, if you need to find the area under a curve that is symmetric about the y-axis, you can calculate the area on one side and double it.
• Visualizing Graphs: Symmetry helps in visualizing the graph of an equation. Knowing the type of symmetry allows you to sketch the graph more accurately.
• Solving Equations: Symmetry can provide insights into the solutions of equations. For example, if an equation is symmetric about the origin, you know that if (x, y) is a solution, then (-x, -y) is also a solution.

Example:

Suppose you have a curve defined by the equation ##y = x^3 – 4x##. You want to find the points where the curve intersects the x-axis. This curve is symmetric about the origin. To find the x-intercepts, set y = 0: ### 0 = x^3 – 4x ### ### 0 = x(x^2 – 4) ### ### 0 = x(x – 2)(x + 2) ###

The x-intercepts are x = 0, x = 2, and x = -2. Since the curve is symmetric about the origin, if (2, 0) is a point, then (-2, 0) must also be a point, which confirms our solution.

Practice Problems

To reinforce your understanding, try these practice problems:

1. Determine the type of symmetry for the following equations:
   • ##y = x^4 – 3x^2 + 1##
   • ##y = x^3 + 2x##
   • ##x^2 + 4y^2 = 16##
   • ##y = \\\\frac{1}{x^2}##
   • ##y = 3x – 5##
2. Find the reflection of the point (3, -5) across:
   • The x-axis
   • The y-axis
   • The origin
   • The line y = x
   • The line y = -x
3. Sketch the graph of the equation ##y = x^2 – 9## and identify its symmetry.
4. If the point (a, b) lies on a curve that is symmetric about the y-axis, what other point must also lie on the curve?
5. If the point (p, q) lies on a curve that is symmetric about the line y = x, what other point must also lie on the curve?

Answers to Practice Problems

1. • ##y = x^4 – 3x^2 + 1##: Symmetric about the y-axis.
   • ##y = x^3 + 2x##: Symmetric about the origin.
   • ##x^2 + 4y^2 = 16##: Symmetric about the x-axis, y-axis, and origin.
   • ##y = \\\\frac{1}{x^2}##: Symmetric about the y-axis.
   • ##y = 3x – 5##: No symmetry.
   • (3, -5) across the x-axis: (3, 5)
   • (3, -5) across the y-axis: (-3, -5)
   • (3, -5) across the origin: (-3, 5)
   • (3, -5) across the line y = x: (-5, 3)
   • (3, -5) across the line y = -x: (5, -3)
2. The graph of ##y = x^2 – 9## is a parabola opening upwards, with its vertex at (0, -9). It is symmetric about the y-axis.
3. If (a, b) lies on a curve symmetric about the y-axis, then (-a, b) must also lie on the curve.
4. If (p, q) lies on a curve symmetric about the line y = x, then (q, p) must also lie on the curve.

Conclusion

Congratulations! You’ve now completed this lesson on symmetry in coordinate geometry. You’ve learned about the different types of symmetry, how to identify them, and how they can be used to solve problems and analyze equations. Remember that understanding symmetry is a valuable skill that will enhance your ability to work with geometric shapes and equations. Keep practicing, and you’ll become proficient in recognizing and utilizing symmetry in various mathematical contexts. This knowledge of symmetry in coordinate geometry will be beneficial for your future studies.

---