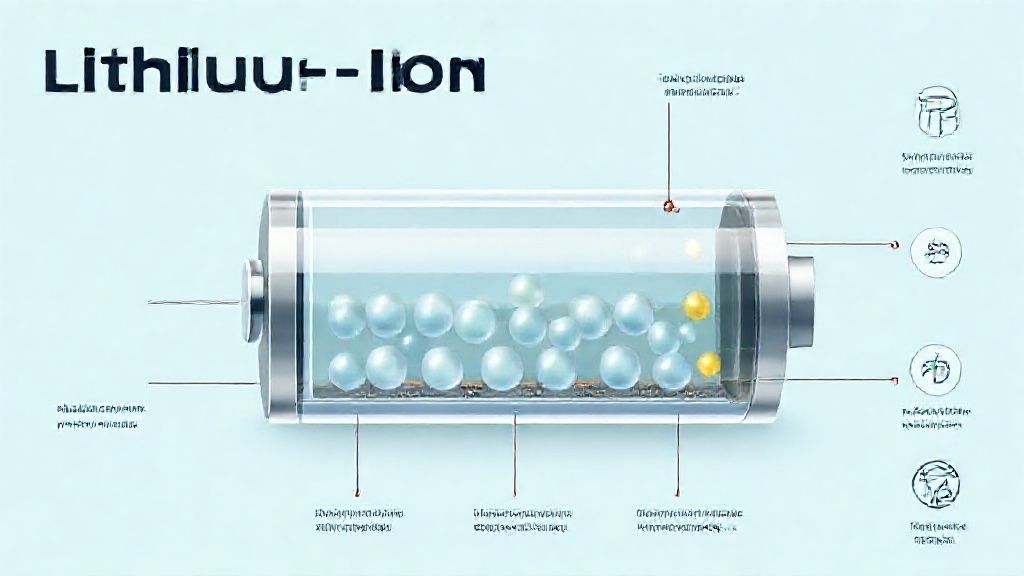
Unpacking Power: A Comprehensive Guide to Lithium-Ion Batteries and Safe Usage
Understand lithium-ion batteries from the inside out: core working principle, common chemistries (LCO/NMC/LFP), performance metrics (Wh vs mAh), battery aging, and essential safety practices to prevent overheating and thermal runaway.



0 Comments