This lesson delves into the heart of coordinate geometry, focusing on the equations that define circles. Understanding these equations is crucial for various mathematical and real-world applications. We will explore the standard form, the general form, and how to derive these equations, along with plenty of examples to solidify your understanding.

We’ll begin by establishing a clear understanding of what a circle actually is. Then, we’ll move on to the different forms of Equations of Circles, like the standard and general forms, and how to use them. Moreover, we’ll work through plenty of examples to help you grasp these concepts.

Understanding the Basics: What is a Circle?

Before diving into equations, let’s establish a clear understanding of what a circle is. A circle is a two-dimensional shape defined as the set of all points equidistant from a central point. This distance is called the radius, and the central point is the center of the circle. Think of it as drawing a shape with a compass; the fixed point of the compass is the center, and the distance from the point of the compass to the pencil is the radius.

The Standard Form of the Equation of a Circle

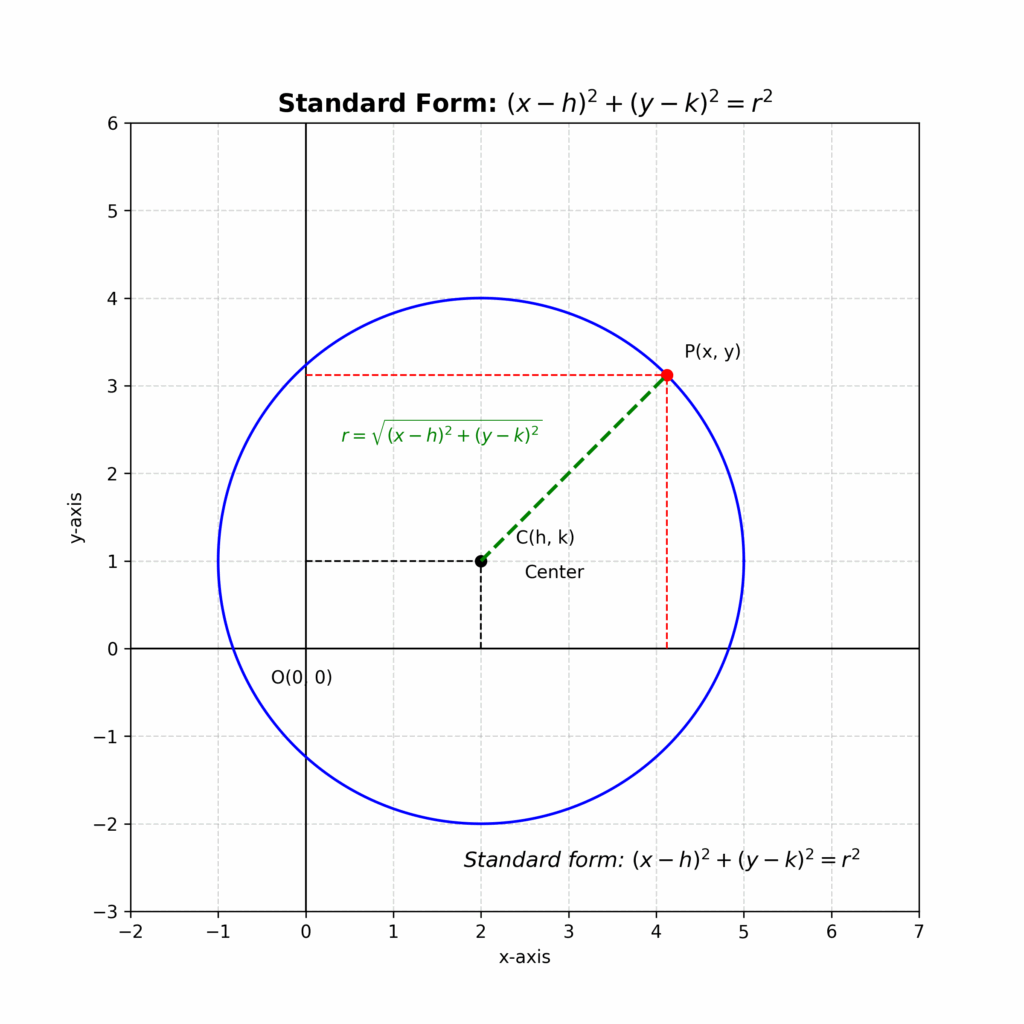
The standard form of the equation of a circle is the most straightforward way to represent a circle in coordinate geometry. It provides direct information about the circle’s center and radius. The standard form is:

### (x – h)^2 + (y – k)^2 = r^2 ###

Where:

• (h, k) represents the coordinates of the center of the circle.
• r represents the radius of the circle.

This equation is derived from the distance formula. Consider any point (x, y) on the circle. The distance between this point and the center (h, k) is always equal to the radius, r. Using the distance formula:

### \sqrt{(x – h)^2 + (y – k)^2} = r ###

Squaring both sides gives us the standard form equation.

Example 1: Finding the Equation from Center and Radius

Let’s say a circle has a center at (2, 3) and a radius of 4. To find its equation, we simply substitute these values into the standard form:

### (x – 2)^2 + (y – 3)^2 = 4^2 ### ### (x – 2)^2 + (y – 3)^2 = 16 ###

This is the equation of the circle.

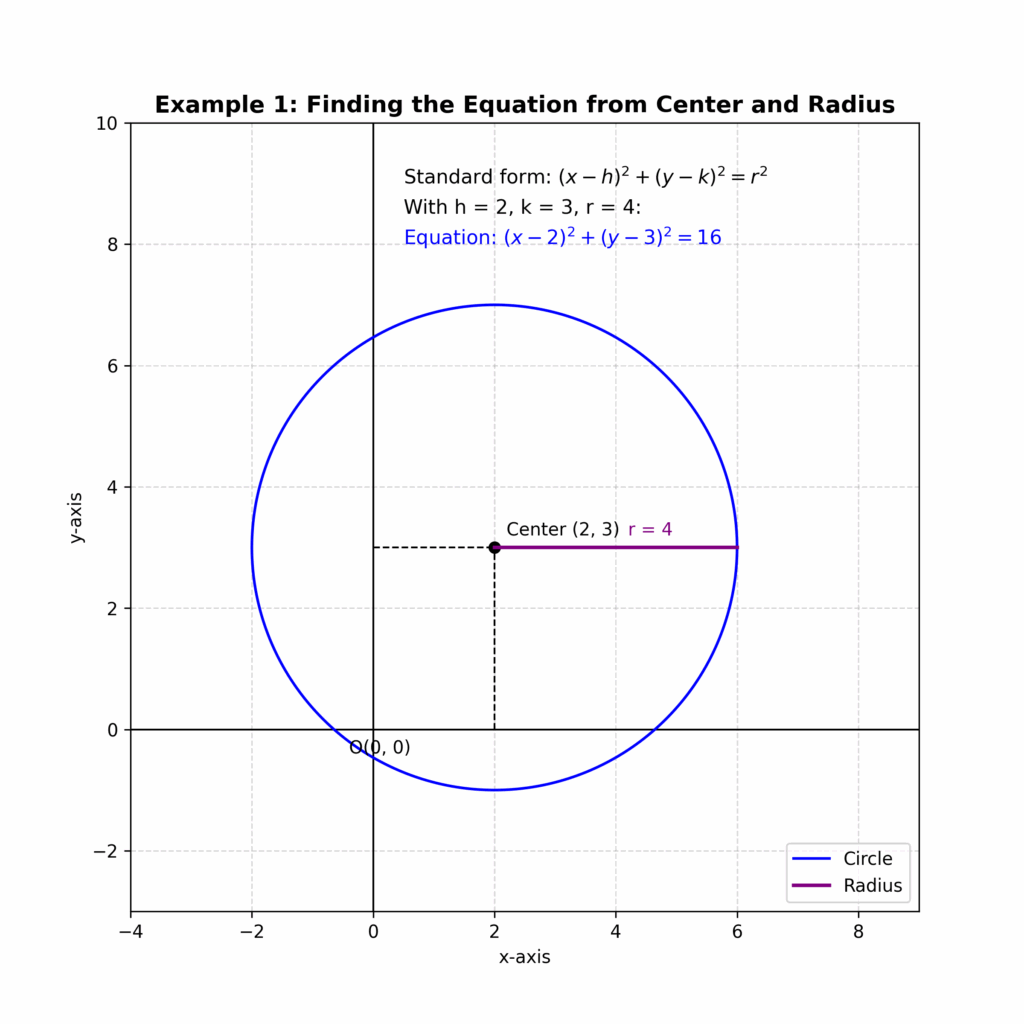
Any point (x, y) that satisfies this equation lies on the circle.

Example 2: Finding the Center and Radius from the Equation

Now, let’s reverse the process. Suppose we have the equation:

### (x + 1)^2 + (y – 5)^2 = 9 ###

To find the center and radius, we compare this equation to the standard form. Notice that (x + 1) can be written as (x – (-1)). Therefore, the center is at (-1, 5), and the radius is ##\sqrt{9} = 3##.

Example 3: A More Complex Scenario

Consider the equation:

### (x – 0)^2 + (y + 2)^2 = 25 ###

This can be rewritten as:

### x^2 + (y – (-2))^2 = 5^2 ###

The center is at (0, -2), and the radius is 5. This is a circle centered on the y-axis.

The General Form of the Equation of a Circle

The general form of the equation of a circle is another way to represent a circle. It is often encountered when the equation is not immediately in standard form. The general form is:

### x^2 + y^2 + 2gx + 2fy + c = 0 ###

Where g, f, and c are constants. The center and radius can be derived from the coefficients in this form. The center is at (-g, -f), and the radius is ##\sqrt{g^2 + f^2 – c}##.

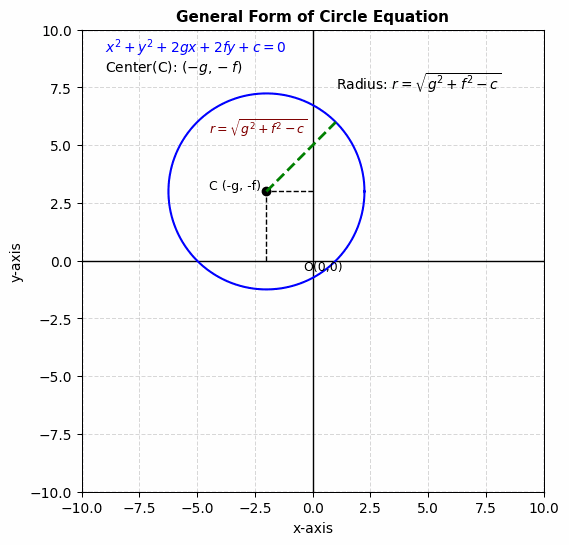
✅ So what is g and f?

They are:

Symbol	Meaning
g	Negative of the x-coordinate of the circle’s center
f	Negative of the y-coordinate of the circle’s center
c	Constant; used in radius calculation: g2+f2−c\sqrt{g^2 + f^2 – c}

Deriving the General Form from the Standard Form

To see how the general form arises, let’s expand the standard form:

### (x – h)^2 + (y – k)^2 = r^2 ###### x^2 – 2hx + h^2 + y^2 – 2ky + k^2 = r^2 ###### x^2 + y^2 – 2hx – 2ky + (h^2 + k^2 – r^2) = 0 ###

Now, let’s make the following substitutions:

• g = -h
• f = -k
• c = h^2 + k^2 – r^2

Substituting these into the expanded standard form gives us the general form:

### x^2 + y^2 + 2gx + 2fy + c = 0 ###

Example 4: Converting from General Form to Standard Form

Let’s say we have the equation:

### x^2 + y^2 + 6x – 4y + 4 = 0 ###

To find the center and radius, we need to convert this to standard form. We do this by completing the square.

First, group the x and y terms:

### (x^2 + 6x) + (y^2 – 4y) = -4 ###

Now, complete the square for the x terms. Take half of the coefficient of x (which is 6), square it (##(6/2)^2 = 9##), and add it to both sides. Do the same for the y terms. Take half of the coefficient of y (which is -4), square it (##(-4/2)^2 = 4##), and add it to both sides:

### (x^2 + 6x + 9) + (y^2 – 4y + 4) = -4 + 9 + 4 ###### (x + 3)^2 + (y – 2)^2 = 9 ###

Now, the equation is in standard form. The center is at (-3, 2), and the radius is ##\sqrt{9} = 3##.

Example 5: Another General Form Example

Consider the equation:

### x^2 + y^2 – 8x + 10y + 37 = 0 ###

Complete the square:

### (x^2 – 8x) + (y^2 + 10y) = -37 ###### (x^2 – 8x + 16) + (y^2 + 10y + 25) = -37 + 16 + 25 ###### (x – 4)^2 + (y + 5)^2 = 4 ###

The center is at (4, -5), and the radius is ##\sqrt{4} = 2##.

Example 6: Using the Formulas Directly

Let’s use the formulas for the center and radius directly from the general form. Consider the equation:

### x^2 + y^2 – 2x + 4y – 4 = 0 ###

Here, 2g = -2, so g = -1. 2f = 4, so f = 2. c = -4.

The center is at (-g, -f) = (1, -2).

The radius is ##\sqrt{g^2 + f^2 – c} = \sqrt{(-1)^2 + 2^2 – (-4)} = \sqrt{1 + 4 + 4} = \sqrt{9} = 3##.

Finding the Equation of a Circle Given Different Conditions

The beauty of the equations of circles lies in their versatility. You can determine the equation of a circle given various pieces of information.

Case 1: Given the endpoints of a diameter

If you are given the endpoints of a diameter, you can find the equation of the circle. The midpoint of the diameter is the center of the circle, and half the length of the diameter is the radius.

Example 7: Diameter Endpoints

Suppose the endpoints of a diameter are A(1, 2) and B(5, 8). First, find the midpoint (the center):

### Center = (\frac{x_1 + x_2}{2}, \frac{y_1 + y_2}{2}) ###### Center = (\frac{1 + 5}{2}, \frac{2 + 8}{2}) = (3, 5) ###

Next, find the radius. The radius is half the distance between A and B. Use the distance formula:

### Distance AB = \sqrt{(x_2 – x_1)^2 + (y_2 – y_1)^2} ###### Distance AB = \sqrt{(5 – 1)^2 + (8 – 2)^2} = \sqrt{4^2 + 6^2} = \sqrt{16 + 36} = \sqrt{52} ###### Radius = \frac{\sqrt{52}}{2} ###

Now, use the standard form:

### (x – 3)^2 + (y – 5)^2 = (\frac{\sqrt{52}}{2})^2 ###### (x – 3)^2 + (y – 5)^2 = 13 ###

Case 2: Given the center and a point on the circle

If you know the center and a point on the circle, you can find the radius (the distance between the center and the point) and then use the standard form.

Example 8: Center and a Point

Let the center be (0, 0) and a point on the circle be (3, 4). The radius is the distance between these two points:

### Radius = \sqrt{(3 – 0)^2 + (4 – 0)^2} = \sqrt{3^2 + 4^2} = \sqrt{9 + 16} = \sqrt{25} = 5 ###

The equation is:

### (x – 0)^2 + (y – 0)^2 = 5^2 ###### x^2 + y^2 = 25 ###

Case 3: Given three points on the circle

Finding the equation of a circle given three points is a bit more involved. You can use the general form and substitute the coordinates of the three points to create a system of three equations. Solving this system will give you the values of g, f, and c, allowing you to determine the center and radius.

Example 9: Three Points

Suppose the three points are A(1, 1), B(2, -1), and C(3, 1). Substitute these points into the general form:

For point A(1, 1):

### 1^2 + 1^2 + 2g(1) + 2f(1) + c = 0 ###### 2 + 2g + 2f + c = 0 (Equation 1) ###

For point B(2, -1):

### 2^2 + (-1)^2 + 2g(2) + 2f(-1) + c = 0 ###### 5 + 4g – 2f + c = 0 (Equation 2) ###

For point C(3, 1):

### 3^2 + 1^2 + 2g(3) + 2f(1) + c = 0 ###### 10 + 6g + 2f + c = 0 (Equation 3) ###

Now, solve this system of equations. Subtract Equation 1 from Equation 3:

### (10 + 6g + 2f + c) – (2 + 2g + 2f + c) = 0 ###### 8 + 4g = 0 ###### g = -2 ###

Substitute g = -2 into Equation 1:

### 2 + 2(-2) + 2f + c = 0 ###### -2 + 2f + c = 0 (Equation 4) ###

Substitute g = -2 into Equation 2:

### 5 + 4(-2) – 2f + c = 0 ###### -3 – 2f + c = 0 (Equation 5) ###

Subtract Equation 5 from Equation 4:

### (-2 + 2f + c) – (-3 – 2f + c) = 0 ###### 1 + 4f = 0 ###### f = -1/4 ###

Substitute f = -1/4 into Equation 4:

### -2 + 2(-1/4) + c = 0 ###### -2 – 1/2 + c = 0 ###### c = 5/2 ###

So, g = -2, f = -1/4, and c = 5/2. The center is at (-g, -f) = (2, 1/4). The radius is ##\sqrt{g^2 + f^2 – c} = \sqrt{(-2)^2 + (-1/4)^2 – 5/2} = \sqrt{4 + 1/16 – 5/2} = \sqrt{27/16} = \frac{\sqrt{27}}{4}##.

The general equation is:

### x^2 + y^2 – 4x – \frac{1}{2}y + \frac{5}{2} = 0 ###

Tangents and Normals to a Circle

Understanding tangents and normals is essential for a deeper understanding of circles. A tangent is a line that touches the circle at exactly one point, and a normal is a line perpendicular to the tangent at the point of tangency. The normal always passes through the center of the circle.

Finding the Equation of a Tangent

To find the equation of a tangent, you need a point on the circle and the slope of the radius to that point. The tangent is perpendicular to the radius at the point of tangency. Therefore, the slope of the tangent is the negative reciprocal of the slope of the radius.

Example 10: Finding the Tangent

Consider the circle ##x^2 + y^2 = 25##. Find the equation of the tangent at the point (3, 4).

The center of the circle is (0, 0). The slope of the radius connecting (0, 0) and (3, 4) is ##\frac{4-0}{3-0} = \frac{4}{3}##.

The slope of the tangent is the negative reciprocal of ##\frac{4}{3}##, which is ##-\frac{3}{4}##.

Use the point-slope form of a line: ##y – y_1 = m(x – x_1)##, where m is the slope and (x1, y1) is the point on the line.

### y – 4 = -\frac{3}{4}(x – 3) ###### y – 4 = -\frac{3}{4}x + \frac{9}{4} ###### y = -\frac{3}{4}x + \frac{25}{4} ###### 4y = -3x + 25 ###### 3x + 4y – 25 = 0 ###

This is the equation of the tangent line.

Finding the Equation of a Normal

The normal is perpendicular to the tangent and passes through the center of the circle. The slope of the normal is the same as the slope of the radius to the point of tangency.

Example 11: Finding the Normal

Using the same circle and point as in Example 10, the slope of the radius is ##\frac{4}{3}##.

The equation of the normal is:

### y – 4 = \frac{4}{3}(x – 3) ###### y – 4 = \frac{4}{3}x – 4 ###### y = \frac{4}{3}x ###### 3y = 4x ###### 4x – 3y = 0 ###

Circles and Other Geometric Shapes

Circles often interact with other geometric shapes, such as lines, other circles, and conic sections. Understanding how to find the points of intersection and analyze these relationships is important.

Intersection of a Circle and a Line

To find the points of intersection between a circle and a line, you need to solve the system of equations formed by the equation of the circle and the equation of the line. This often involves substituting one equation into the other and solving for the remaining variable.

Example 12: Intersection of a Circle and a Line

Consider the circle ##x^2 + y^2 = 25## and the line ##y = x + 1##. Substitute the equation of the line into the equation of the circle:

### x^2 + (x + 1)^2 = 25 ###### x^2 + x^2 + 2x + 1 = 25 ###### 2x^2 + 2x – 24 = 0 ###### x^2 + x – 12 = 0 ###### (x + 4)(x – 3) = 0 ###

So, x = -4 or x = 3. Now, find the corresponding y values using the equation of the line:

If x = -4, then y = -4 + 1 = -3. The point is (-4, -3).

If x = 3, then y = 3 + 1 = 4. The point is (3, 4).

The points of intersection are (-4, -3) and (3, 4).

Intersection of Two Circles

To find the points of intersection between two circles, you can solve the system of equations formed by the equations of the two circles. This can be done by subtracting one equation from the other to eliminate the squared terms, then solving the resulting linear equation along with one of the original circle equations.

Example 13: Intersection of Two Circles

Consider the circles: ##x^2 + y^2 = 25## and ##(x – 1)^2 + y^2 = 16##. Expand the second equation:

### x^2 – 2x + 1 + y^2 = 16 ###

Subtract the first equation from the expanded second equation:

### (x^2 – 2x + 1 + y^2) – (x^2 + y^2) = 16 – 25 ###### -2x + 1 = -9 ###### -2x = -10 ###### x = 5 ###

Substitute x = 5 into the first equation:

### 5^2 + y^2 = 25 ###### 25 + y^2 = 25 ###### y^2 = 0 ###### y = 0 ###

The point of intersection is (5, 0). Note: In this case, the circles only intersect at one point. This means they are tangent to each other.

Applications of Equations of Circles

The “Equations of Circles” have numerous applications in various fields, demonstrating their importance beyond pure mathematics.

• Engineering: Designing circular structures, such as bridges, tunnels, and wheels.
• Computer Graphics: Creating and manipulating circular shapes in 2D and 3D graphics.
• Physics: Modeling the motion of objects in circular paths.
• Navigation: Determining the position of objects using circular arcs.
• Astronomy: Describing the orbits of planets and other celestial bodies.

Advanced Topics and Further Exploration

This lesson has provided a solid foundation in the equations of circles. For further exploration, consider these advanced topics:

• Conic Sections: Ellipses, parabolas, and hyperbolas are closely related to circles.
• Polar Coordinates: Representing circles using polar coordinates.
• 3D Geometry: Extending the concepts to spheres and other 3D shapes.
• Calculus: Applying calculus concepts to circles, such as finding the area and circumference.

Conclusion

Congratulations! You’ve completed this comprehensive lesson on the equations of circles. You now have a strong understanding of the standard and general forms, how to derive them, and how to apply them to solve various problems. Remember to practice regularly to solidify your knowledge. The “Equations of Circles” are a fundamental concept in coordinate geometry, and mastering them will serve you well in your mathematical journey. Keep practicing, and you’ll become proficient in working with circles!