ADVERTISEMENT
Find \( \lim_{x \to 3} (2x + 5) \)
Solution:
To solve this limit, we substitute the value of \( x \) directly because the function is continuous at \( x = 3 \).
\( \lim_{x \to 3} (2x + 5) = 2(3) + 5 = 6 + 5 = 11 \)
Inserting an insulating material between its plates drastically changes the capacitance, stored energy, and potential...
Explore projectile motion on an inclined plane with detailed derivations, conditions for perpendicular impact, solved examples, and a Python simulation.
Rutherford atomic model explains the nuclear structure of the atom with a bold claim: nearly all mass and positive...
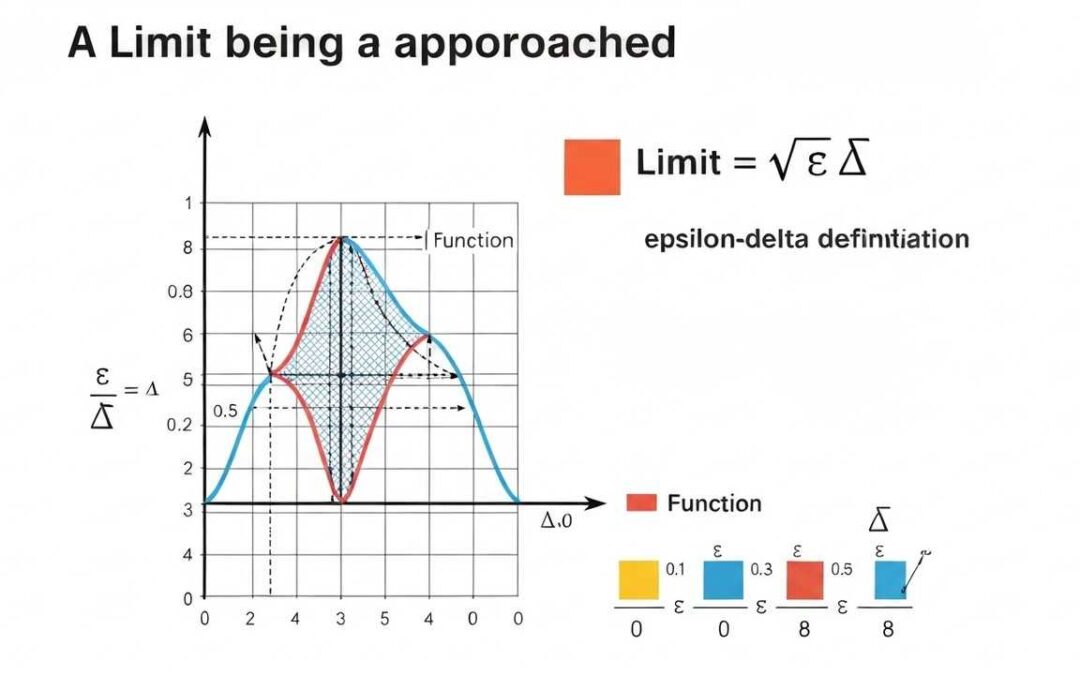
Understanding **limits of functions** is essential in calculus. This guide explains the epsilon-delta definition, theorems, and applications to help you master this fundamental concept.
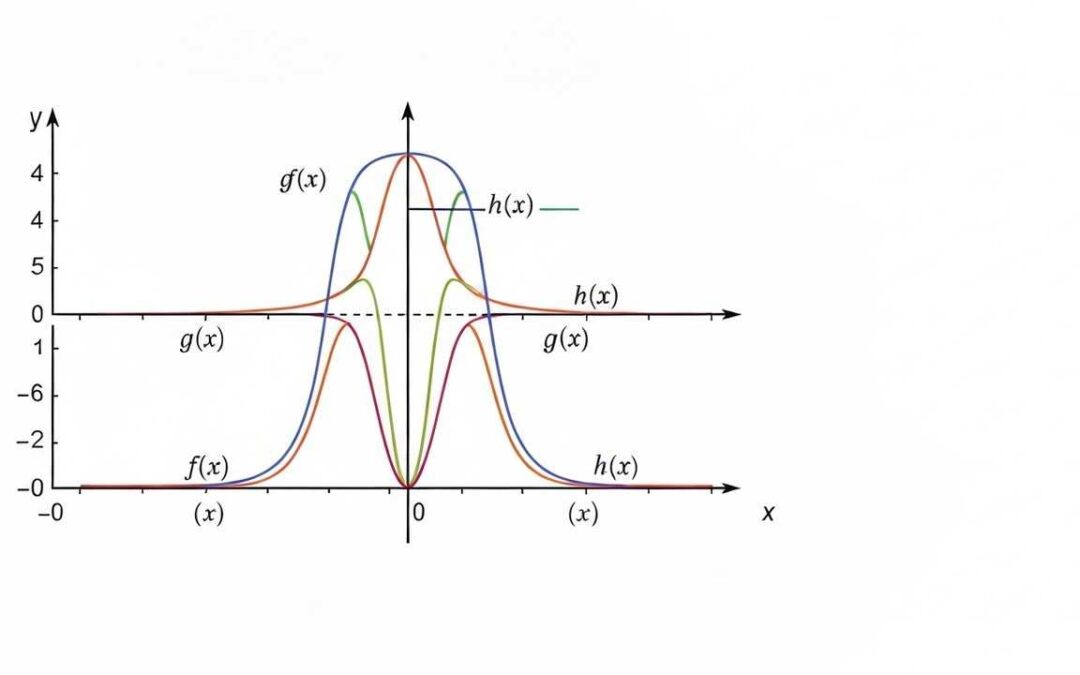
The Squeeze Theorem is a calculus concept that uses bounding functions to determine the limit of a function. The article explains how it works and provides examples.
Learn how to solve Evaluating Limits Problems with this step-by-step guide. We’ll cover the fundamentals and provide clear examples.
Learn how to solve Limits at Infinity with this comprehensive guide. Understand the concepts and techniques through clear examples and step-by-step solutions.
Hi there,
My name is Mike from Monkey Digital,
Allow me to present to you a lifetime revenue opportunity of 35%
That’s right, you can earn 35% of every order made by your affiliate for life.
Simply register with us, generate your affiliate links, and incorporate them on your website, and you are done. It takes only 5 minutes to set up everything, and the payouts are sent each month.
Click here to enroll with us today:
https://www.monkeydigital.org/affiliate-dashboard/
Think about it,
Every website owner requires the use of search engine optimization (SEO) for their website. This endeavor holds significant potential for both parties involved.
Thanks and regards
Mike Miers
Monkey Digital