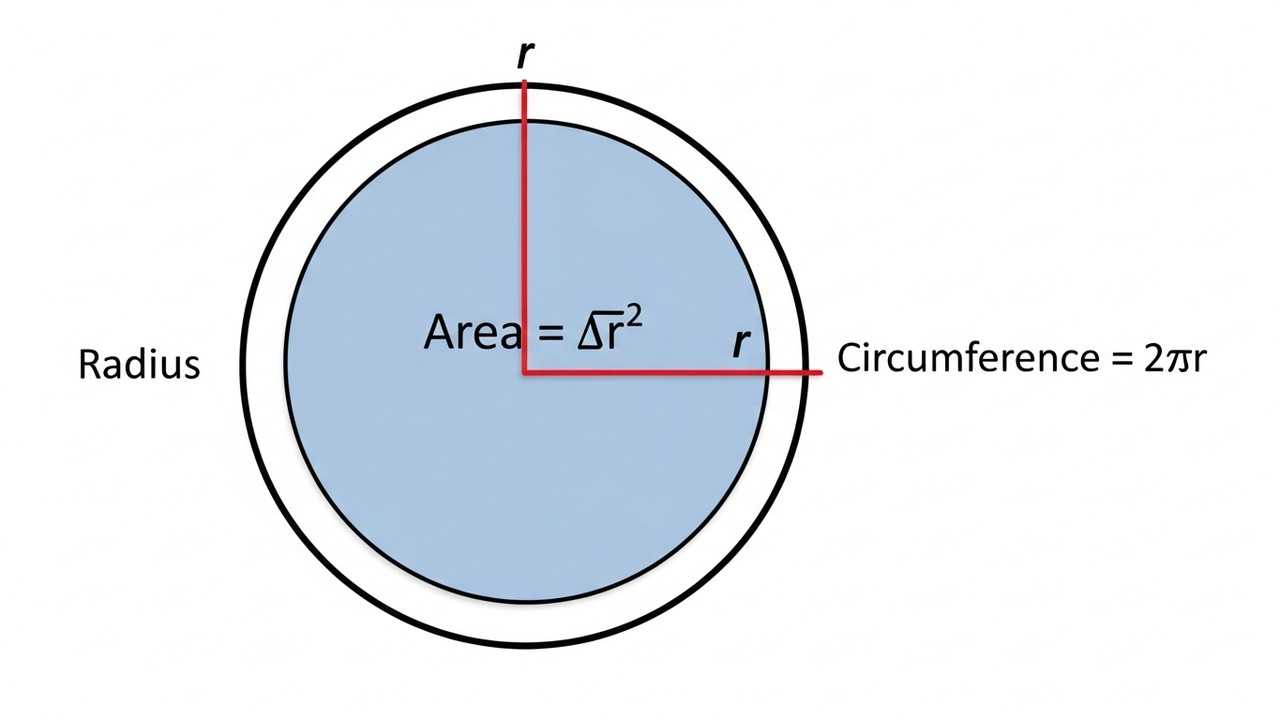
The circle area and circumference are two fundamental concepts in geometry. They describe the space a circle occupies and the distance around it, respectively. This blog post will delve into these concepts, providing a clear explanation of how to calculate the area and circumference of a circle when the radius is given. We will utilize the basic formulas.
Table of Contents
- Calculating the Area
- Calculating the Circumference
- Similar Problems and Quick Solutions
- Problem 1: A circle has a radius of 10 cm. Find its area.
- Problem 2: A circle has a diameter of 14 cm. Find its circumference.
- Problem 3: Find the area of a circle with a diameter of 20 cm.
- Problem 4: If the circumference of a circle is 62.8 cm, find its radius.
- Problem 5: Calculate the area of a circle with a radius of 5 cm.
Read More
Let’s explore the concepts of area and circumference related to circles. Understanding these fundamental geometric properties is crucial in various fields, from architecture to physics. This blog post will guide you through calculating these values, using the given radius of a circle, with clear explanations and examples. The circle area and circumference are essential in geometry.
Understanding Circle Area and Circumference
The problem involves calculating the area and circumference of a circle. The area represents the space enclosed within the circle, while the circumference is the total distance around its edge. Both are directly related to the radius, which is the distance from the center of the circle to any point on its edge. The formulas for these calculations are fundamental.
To solve this, we’ll use the standard formulas for the area and circumference of a circle. The area (A) is given by ##A = \pi r^2##, where ‘r’ is the radius, and ##\pi## (pi) is a mathematical constant approximately equal to 3.14159. The circumference (C) is given by ##C = 2\pi r##. We will be using these formulas to determine the circle area and circumference.
Calculating the Area
Step 1: Applying the Formula
We are given that the radius (r) of the circle is 7 cm. Using the formula for the area of a circle, ##A = \pi r^2##, we substitute the given value of the radius. This step is straightforward, involving only the substitution of the radius value into the formula, ensuring that we maintain the correct units. This is a key step to find the circle area and circumference.
Substituting r = 7 cm, we get ##A = \pi (7)^2##. This simplifies to ##A = 49\pi## square centimeters. To get a numerical value, we can use the approximate value of ##\pi##, which is approximately 3.14159. Make sure to correctly use the formula for circle area and circumference.
Step 2: Calculating the Area
Multiplying 49 by ##\pi## gives us the area. Using ##\pi \approx 3.14159##, we calculate ##A \approx 49 \times 3.14159##. This results in approximately 153.938 square centimeters. The area calculation is complete once we have the value of the area. The circle area and circumference are the main focus here.
Therefore, the area of the circle is approximately 153.938 square centimeters. We have successfully calculated the area, now we move on to finding the circumference. The circle area and circumference are two important features of a circle.
Calculating the Circumference
Step 1: Applying the Formula
Using the formula for the circumference of a circle, ##C = 2\pi r##, and substituting the radius (r = 7 cm), we get ##C = 2 \times \pi \times 7##. This is a direct application of the formula, ensuring the radius is correctly used. This is another step to find the circle area and circumference.
Simplifying the equation, we have ##C = 14\pi## centimeters. Again, we can use the approximation ##\pi \approx 3.14159## to find the numerical value of the circumference. Remember to include the correct units in your calculations. This is also important for the circle area and circumference.
Step 2: Calculating the Circumference
Multiplying 14 by ##\pi## gives us the circumference. Using ##\pi \approx 3.14159##, we calculate ##C \approx 14 \times 3.14159##. This results in approximately 43.982 centimeters. The circumference is the total distance around the circle. Always remember to calculate the circle area and circumference.
Therefore, the circumference of the circle is approximately 43.982 centimeters. We have now calculated both the area and the circumference. These values are fundamental to understanding the properties of a circle. Now, we have calculated the circle area and circumference.
Final Solution
Area of the circle: ##A \approx 153.938 cm^2##. Circumference of the circle: ##C \approx 43.982 cm##
Similar Problems and Quick Solutions
Problem 1: A circle has a radius of 10 cm. Find its area.
Area = ##\pi (10)^2 \approx 314.159 cm^2##
Problem 2: A circle has a diameter of 14 cm. Find its circumference.
Circumference = ##\pi \times 14 \approx 43.982 cm##
Problem 3: Find the area of a circle with a diameter of 20 cm.
Area = ##\pi (10)^2 \approx 314.159 cm^2##
Problem 4: If the circumference of a circle is 62.8 cm, find its radius.
Radius ≈ 10 cm
Problem 5: Calculate the area of a circle with a radius of 5 cm.
Area ≈ 78.54 cm²
| Property | Formula | Calculation | Result |
|---|---|---|---|
| Radius | Given | r = 7 cm | 7 cm |
| Area | ##A = \pi r^2## | ##A = \pi (7)^2 \approx 49 \times 3.14159## | ##A \approx 153.938 cm^2## |
| Circumference | ##C = 2\pi r## | ##C = 2 \times \pi \times 7 \approx 14 \times 3.14159## | ##C \approx 43.982 cm## |
We also Published
RESOURCES
- Why is the derivative of a circle’s area its circumference? : r/askscience
- Finding the Area & Circumference of a Circle – Lesson | Study.com
- Are the formulas for both the circumference and area of a circle …
- Circumference and Area of a Circle Calculator
- Area and circumference of circles | 8th grade math – IXL
- Circles: area & circumference | Khan Academy
- 11-Circumference and Area of Circles.pdf
- 3.2.3: Relating Area to Circumference – Mathematics LibreTexts
- Area of a Circle – Formula, Derivation, Examples
- Area of a circle – Wikipedia






0 Comments