Adiabatic expansion work is a fundamental concept in thermodynamics, crucial for understanding how energy transforms in systems. You’ll learn to calculate the work done by or on a gas during expansion or compression without any heat exchange. This knowledge is vital for solving problems in physics and engineering, giving you a deeper understanding of energy conservation.
Table of Contents
Read More
What is Adiabatic Expansion?
Adiabatic expansion occurs when a gas expands without exchanging heat with its environment. Imagine a perfectly insulated container where a gas is allowed to expand. As the gas expands, it pushes against a piston, performing work. Since no heat is added or removed, the internal energy of the gas changes solely due to the work done.
Defining Adiabatic Process
An adiabatic process is a thermodynamic process where no heat transfer occurs between the system and its surroundings. This means that the system is perfectly insulated or that the process happens so quickly that there is no time for heat transfer. The key characteristic of an adiabatic process is ##Q = 0##, where Q represents the heat exchanged.
In such scenarios, the First Law of Thermodynamics simplifies significantly. The First Law states that ##ΔU = Q – W##, where ##ΔU## is the change in internal energy, Q is the heat added to the system, and W is the work done by the system.
Because ##Q = 0## in an adiabatic process, the equation becomes ##ΔU = -W##.
This equation directly links the change in internal energy to the work done. If the gas expands (and does work), its internal energy decreases. Conversely, if work is done on the gas (compression), its internal energy increases. This direct relationship is a cornerstone of understanding adiabatic processes.
Temperature Changes During Expansion
As a gas expands adiabatically, its temperature decreases. This occurs because the gas molecules use their internal energy to do work against the external pressure. Since the total energy of the system is conserved (no heat exchange), the decrease in internal energy results in a drop in temperature. This is a fundamental concept in thermodynamics.
The relationship between temperature (T), pressure (P), and volume (V) during an adiabatic process is described by the following equation: ##PV^γ = constant##, where γ (gamma) is the adiabatic index, which depends on the gas’s specific heat capacities.
For a monatomic ideal gas, ##γ = 5/3##, and for a diatomic ideal gas, ##γ = 7/5##.
This equation helps us understand how pressure and volume change during the process, which in turn affects the temperature. For example, if the volume increases (expansion), the pressure decreases, and consequently, the temperature drops. This principle is used in various applications, such as the cooling of gases in refrigerators and the expansion of gases in engines.
Calculating Adiabatic Expansion Work
To calculate the work done during an adiabatic process, we use the First Law of Thermodynamics, ##ΔU = -W##. If the internal energy change (##ΔU##) is known, the work done (W) can be directly calculated. The sign of W indicates whether work is done by the gas (negative ##ΔU##, expansion) or on the gas (positive ##ΔU##, compression).
Problem: Adiabatic Expansion of a Gas
Consider a gas undergoing adiabatic expansion. The internal energy of the gas decreases by 150 J. Calculate the work done by or on the gas.
Solution: Applying the First Law
Given: ##ΔU = -150 J##. Using the First Law for an adiabatic process, ##ΔU = -W##. Therefore, ##-150 J = -W##, which gives us ##W = 150 J##. The work done by the gas is 150 J. This means the gas has done work on its surroundings, and its internal energy has decreased as a result.
In this problem, the negative change in internal energy (##ΔU = -150 J##) indicates that the gas is expanding and doing work on its surroundings. The work done is positive (##W = 150 J##), signifying that the gas is indeed performing work. This result emphasizes the direct relationship between the change in internal energy and the work done in an adiabatic process.
The gas has expanded, converting its internal energy into work. This concept is crucial in understanding the energy transformations in various systems. If the internal energy had increased, the work would have been negative, indicating work being done on the gas (compression).
Numerical Problems
Problem 1
A gas expands adiabatically and does 200 J of work. What is the change in internal energy?
Problem 2
During an adiabatic compression, the internal energy increases by 100 J. How much work is done?
Problem 3
A gas expands without heat transfer, and its internal energy decreases by 50 J. Calculate the work done.
Problem 4
If a gas is compressed adiabatically, and 75 J of work is done on it, what is the change in internal energy?
Problem 5
A system undergoes adiabatic expansion, resulting in a 20 K decrease in temperature. What can you infer about the work done?
Adiabatic Processes (##Q=0##): Quick Solutions, Tables, and Diagram
For any adiabatic change, heat transfer is zero (##Q=0##). The First Law reduces to:
###\Delta U = Q – W = -\,W###
We use the sign convention “work by the system” is positive (##W>0##). Thus, during adiabatic expansion (##W>0##) the internal energy decreases (##\Delta U<0##); during adiabatic compression (##W<0##) the internal energy increases (##\Delta U>0##).
Worked Problems
Problem 1
Prompt. A gas expands adiabatically and does 200 J of work. What is the change in internal energy?
Computation. ###\Delta U = -W = -200\ \text{J}###
Solution. ##\Delta U = -200\ \text{J}##
Problem 2
Prompt. During an adiabatic compression, the internal energy increases by 100 J. How much work is done?
Computation. ###\Delta U = -W \Rightarrow W = -\Delta U = -100\ \text{J}### (negative means work is done on the gas)
Solution. ##W = -100\ \text{J}##
Problem 3
Prompt. A gas expands without heat transfer, and its internal energy decreases by 50 J. Calculate the work done.
Computation. ###\Delta U = -50\ \text{J} = -W \Rightarrow W = +50\ \text{J}###
Solution. ##W = 50\ \text{J}## (work by the gas)
Problem 4
Prompt. If a gas is compressed adiabatically, and 75 J of work is done on it, what is the change in internal energy?
Computation. “Work on the gas” → ##W<0## with magnitude 75 J, so ##W=-75\ \text{J}##. Then ###\Delta U = -W = -(-75) = +75\ \text{J}###
Solution. ##\Delta U = +75\ \text{J}##
Problem 5
Prompt. A system undergoes adiabatic expansion, resulting in a 20 K decrease in temperature. What can you infer about the work done?
Reasoning. For an ideal gas, internal energy depends on temperature only. A drop in ##T## implies ##\Delta U<0##, hence ###W = -\Delta U > 0###.
Solution. Work is done by the gas (##W>0##)
Summary Table
| Problem | Process | Given | Relation (adiabatic) | Result | Interpretation |
|---|---|---|---|---|---|
| P1 | Expansion | ##W=+200\ \text{J}## | ###\Delta U=-W### | ###\Delta U=-200\ \text{J}### | Internal energy drops |
| P2 | Compression | ##\Delta U=+100\ \text{J}## | ###W=-\Delta U### | ###W=-100\ \text{J}### | Work done on gas |
| P3 | Expansion | ##\Delta U=-50\ \text{J}## | ###W=-\Delta U### | ###W=+50\ \text{J}### | Work by gas |
| P4 | Compression | Work on gas: ##W=-75\ \text{J}## | ###\Delta U=-W### | ###\Delta U=+75\ \text{J}### | Internal energy rises |
| P5 | Expansion | ##\Delta T=-20\ \text{K}## | Ideal gas: ##\Delta U\propto \Delta T## | ###W>0### | Work by gas |
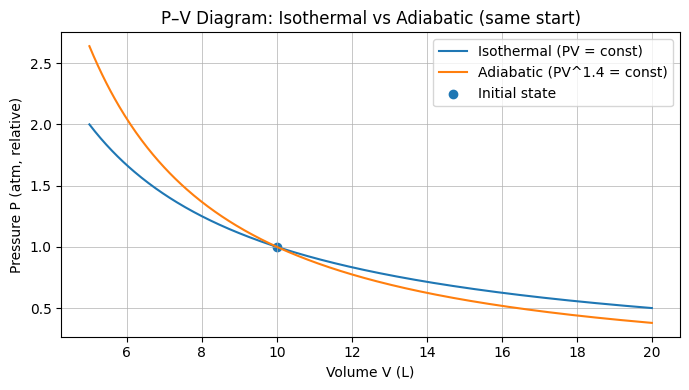
Diagram: Isothermal vs Adiabatic Paths
The adiabatic curve is steeper than the isothermal through the same starting point (here using ##\gamma=1.4##). This reflects that adiabatic expansion cools the gas (no heat inflow), so pressure falls faster with volume than in the isothermal case.
Key Takeaways
Understanding adiabatic expansion work is essential for anyone studying thermodynamics. You’ve seen how to calculate energy changes and explored the relationship between internal energy and work done in the absence of heat transfer. By mastering these concepts, you can apply them to various practical scenarios.
| Concept | Explanation | Equation |
|---|---|---|
| Adiabatic Process | A thermodynamic process where no heat is exchanged with the surroundings. | ##Q = 0## |
| First Law of Thermodynamics (Adiabatic) | The change in internal energy equals the negative of the work done. | ##ΔU = -W## |
| Work Done by the Gas | Gas expands, decreasing internal energy. | ##W > 0##, ##ΔU < 0## |
| Work Done on the Gas | Gas is compressed, increasing internal energy. | ##W < 0##, ##ΔU > 0## |
We also Published
RESOURCES
- Adiabatic process – Wikipedia
- 3.7: Adiabatic Processes for an Ideal Gas – Physics LibreTexts
- 3.6 Adiabatic Processes for an Ideal Gas – University Physics …
- Adiabatic Processes
- 8.4: Reversible Adiabatic Expansion of an Ideal Gas – Physics …
- homework and exercises – Work Done by an Adiabatic Expansion …
- ELI5: Why does the temperature drop in an adiabatic expansion? : r …
- Video: Work Done in an Adiabatic Process
- I am confused about the first and second stages of the Carnot cycle …
- Isothermal and adiabatic expansion



0 Comments